8.2. Надежность при распределении Вейбулла

Наиболее универсальным при моделировании отказов различных объектов является распределение Вейбулла. Это распределение можно рассматривать как обобщение экспоненциального распределения: функция распределения Вейбулла

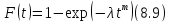
здесь 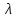> 0 и m > 0 – параметры распределения, подбирая которые можно моделировать любой участок кривой интенсивности отказов.

Вероятность безотказной работы

плотность распределения

интенсивность отказов

В частности при m = 1 имеем экспоненциальное распределение, при m = 2 – распределение Рэлея ( (t) – наклонная прямая), при m < 1 моделируется участок приработки, при m > 2 – процессы старения.

Для проведения расчетов может использоваться встроенной функцией:

ВЕЙБУЛЛ - возвращает распределение Вейбулла. Это распределение используется при анализе надежности, например для вычисления среднего времени наработки на отказ какого-либо устройства.

Синтаксис:

ВЕЙБУЛЛ(x;альфа;бета;интегральная)

Здесь x  — значение, для которого вычисляется функция;

альфа  — параметр распределения;

бета  — параметр распределения;

интегральная  — определяет форму функции.

Замечания:

Если x, альфа или бета не является числом, то функция ВЕЙБУЛЛ возвращает значение ошибки #ЗНАЧ!.

Если x < 0, то функция ВЕЙБУЛЛ возвращает значение ошибки #ЧИСЛО!.

Если альфа ≤ 0 или бета ≤ 0, то функция ВЕЙБУЛЛ возвращает значение ошибки #ЧИСЛО!.

Уравнение для интегральной функции распределения Вейбулла имеет вид (8.9).

Уравнение для функции плотности распределения Вейбулла имеет вид (8.11).

Если альфа = 1, то функция ВЕЙБУЛЛ возвращает экспоненциальное распределение.

Пример:

1 2 3 4

А B Данные Описание 105 Значение, для которого рассчитывается функция 20 Параметр распределения альфа 100 Параметр распределения бета Формула Описание (результат) =ВЕЙБУЛЛ(A2;A3;A4;ИСТИНА) Интегральная функция распределения Вейбулла в соответствии с приведенными выше условиями (0,929581) =ВЕЙБУЛЛ(A2;A3;A4;ЛОЖЬ) Функция плотности распределения Вейбулла в соответствии с приведенными выше условиями (0,035589)

ЗАДАНИЕ

Надежность четырех объектов описывается распределением Вейбулла с параметрами  = 0,001 и m = 1, 2, 2,2 и 2,5. Построить графики вероятности безотказной работы и интенсивности отказов в диапазоне от 0 до 2500 часов с шагом 100 часов (рис. 8.3).

Рис. 8.3. Образец оформления рабочего листа при проведении расчетов надежности при распределении Вейбулла