6.2. Карта экспоненциально взвешенных скользящих средних

Как и карты кумулятивных сумм, контрольные карты экспоненциально взвешенных скользящих средних используются для обнаружения малых постоянных смещений процесса. При контроле среднего значения для t-й подгруппы рассчитывается статистика

где E₀ принимается равным номинальному (целевому) значению оцениваемого показателя качества, – параметр экспоненциального сглаживания, 0 < < 1 (при = 1 получим обычную карту Шухарта), – выборочное среднее.

Процесс считается статистически управляемым, если найденное по формуле (6.4) значение лежит внутри контрольных границ

где – параметр, определяющий положение границ карты; иногда принимают при использовании правила «трех сигма» = 3; – среднеквадратичное отклонение величин , определяемое из формулы

здесь n – объем подгруппы (мгновенной выборки), – внутригрупповая дисперсия.

ЗАДАНИЕ

Данные из предыдущего задания проанализировать с помощью карты экспоненциально взвешенных скользящих средних.

1) Найти значения (ewma), приняв = 0,3. В качестве E₀ использовать общее среднее значение по первым 10 выборкам.

2) Найти исправленные выборочные дисперсии мгновенных выборок, используя встроенную функцию ДИСП и среднее значение дисперсии ().

3) Вычислить дисперсию () и стандартное отклонение по формуле (6.6).

4) Найти положение верхней и нижней контрольной границ, приняв 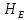= 3.

5) Построить карту экспоненциально взвешенных скользящих средних: обратите внимание на криволинейность контрольных границ на начальном участке карты. В какой выборке обнаружено нарушение?

Рис. 6.3. Образец оформления рабочего листа при построении карты экспоненциально взвешенных скользящих средних

6.3. Многомерная контрольная карта Хотеллинга

Предположим, что в технологическом процессе контролируются р показателей качества

Х = (Х₁ Х₂ … Х_р), имеющих совместное нормальное распределение.

Применение контрольной карты Хотеллинга предполагает расчет для каждой t-й мгновенной выборки (t = 1, ..., m) статистики

где n – объем мгновенной выборки, – вектор средних в мгновенных выборках,

– среднее значение в t-й мгновенной выборке по j-му показателю (j = 1, ..., p); – вектор целевых средних,

где

Оценки компонент ковариационной матрицы размерности , определяющие рассеивание показателей качества и степень тесноты их связи, вычисляются по формуле

При нормальном ходе процесса должно выполняться условие

где 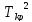– граница критической области.

Многомерная контрольная карта Хотеллинга, по-существу, – та же карта Шухарта, в которой в качестве контролируемой величины используется обобщенная статистика Хотеллинга. Обратим внимание на то, что эта карта имеет только верхнюю контрольную границу.

Если ковариационная матрица Σ известна, статистика Хотеллинга имеет -распределение; в этом случае положение контрольной границы на заданном уровне значимости определяется по таблицам квантилей этого распределения

При оценивании компонент ковариационной матрицы c использованием текущих мгновенных выборок (n > 1) граница критической области определяется по формуле

а для текущих индивидуальных наблюдений по формуле

где – квантиль F-распределения Фишера с числами степеней свободы в числителе k1, в знаменателе – k2.

При проведении расчетов используются статистические функции вычисления среднего СРЗНАЧ, дисперсии ДИСП, ковариации КОВАР, квантилей распределения Фишера ФИШЕРОБР, а также функции массива:

МОБР – возвращает обратную матрицу.

Синтаксис

МОБР(массив)

Массив  — числовой массив с равным количеством строк и столбцов

Замечания

Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.

Если какая-либо из ячеек в массиве пуста или содержит текст, функция МОБР возвращает значение ошибки #ЗНАЧ!.

Функция МОБР также возвращает значение ошибки #ЗНАЧ!, если число строк в массиве не равно числу столбцов.

Формулы, возвращающие массивы, должны быть введены как формулы массива.

Обратные матрицы, как и определители, обычно используются для решения систем уравнений с несколькими неизвестными. Произведение матрицы на ее обратную — это единичная матрица, т. е. квадратный массив, у которого диагональные элементы равны 1, а все остальные — 0.

Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.

Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР возвращает значение ошибки #ЧИСЛО!. Определитель такой матрицы равен 0.

Пример 1

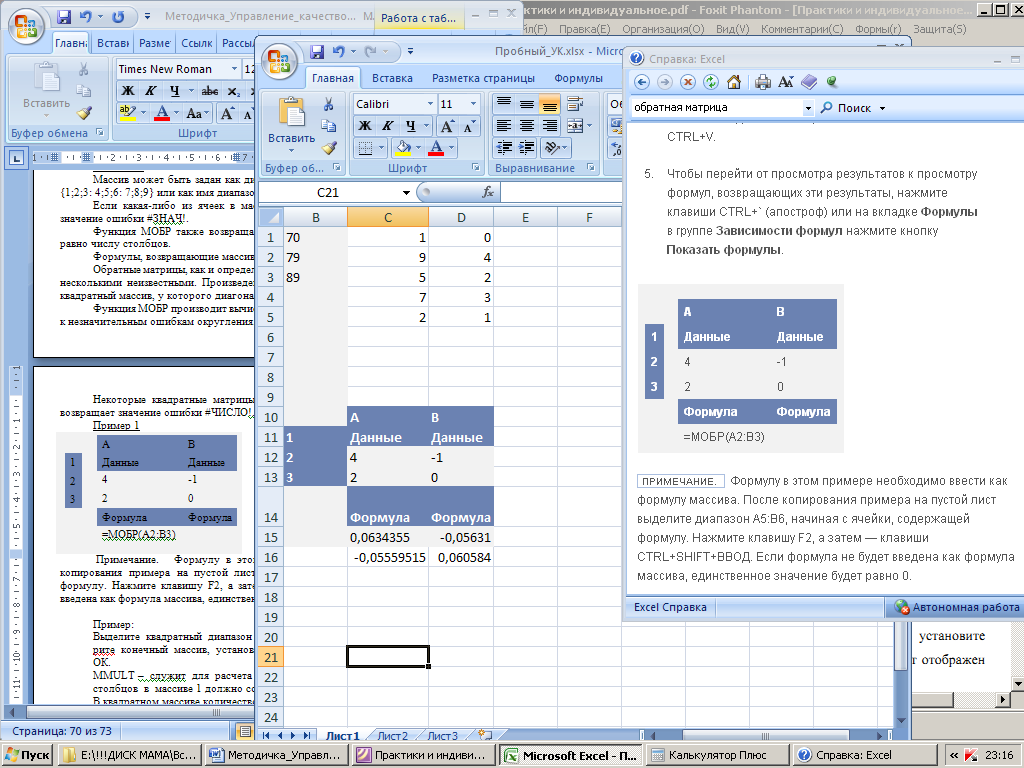
 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон A5:B6, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственное значение будет равно 0.

МУМНОЖ – служит для расчета произведения двух массивов. Количество столбцов в массиве 1 должно совпадать с количеством строк в массиве 2. В квадратном массиве количество строк и столбцов совпадает.

Синтаксис

МУМНОЖ(массив1;массив2)

Массив1, массив2  — перемножаемые массивы.

Замечания

Количество столбцов аргумента массив1 должно совпадать с количеством строк аргумента массив2; при этом оба массива должны содержать только числа.

Массив1 и массив2 могут быть заданы как интервалы, массивы констант или ссылки.

Функция МУМНОЖ возвращает значение ошибки #ЗНАЧ! в следующих случаях:

1. Если какая-либо ячейка пуста или содержит текст.

2. Если число столбцов в аргументе «массив1» отличается от числа строк в аргументе «массив2».

Массив a, который является произведением двух массивов b и c, определяется следующим образом:

где i — номер строки, а j — номер столбца.

Формулы, которые возвращают массивы, должны быть введены как формулы массива.

Пример 2

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон A8:B9, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственное значение будет равно 2.

ТРАНСП – служит для транспонирования строк и столбцов массива.

Синтаксис

ТРАНСП(массив)

Массив  — массив (диапазон ячеек) на рабочем листе, который нужно транспонировать. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая — вторым столбцом и т. д.

Пример 3

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования этого примера на пустой лист выделите диапазон A5:A6, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственное значение будет равно 1.

ЗАДАНИЕ

Контролировалось три показателя качества Х1, Х2, Х3. Сделано 10 выборок по 5 наблюдений в каждой:

1) Вычислить средние значения в каждой мгновенной выборке по каждому из трех показателей (xs).

2) Найти общие средние по всем 10 выборкам (mu0) и разности (xs – mu0).

3) Вычислить дисперсии в каждой мгновенной выборке по каждому из трех показателей (covii) и средние дисперсии (coviis).

4) Вычислить ковариации между каждой парой показателей в каждой мгновенной выборке (cov12, cov23, cov31,) и средние ковариации (covijs).

5) Сформировать ковариационную матрицу S, вычислить обратную матрицу .

6) Вычислить значение статистики Хотеллинга в каждой выборке (6.7). Обратите внимание на особенности записи соответствующей формулы в строке формул на рис. 6.4.

7) Определить критическое значение статистики Хотеллинга (6.11).

8) Используя мастер диаграмм, построить контрольную карту. Оформление провести в соответствии с рис. 6.4.

9) Дать заключение о стабильности процесса.

Рис. 6.4. Образец оформления рабочего листа при построении карты Хотеллинга

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Контролируется отклонение диаметра вала от номинального значения в мкм. Каждые тридцать минут берется выборка по 5 деталей.

Построить карту кумулятивных сумм и проанализировать процесс с использованием V-маски.

2. В условиях предыдущей задачи построить карту экспоненциально взвешенных скользящих средних.

3. Даны матрицы

Используя встроенные функции массива, вычислить выражение

ЛАБОРАТОРНАЯ РАБОТА № 7. ВЫБОРОЧНЫЙ КОНТРОЛЬ ПРИ ПРИЕМКЕ ПРОДУКЦИИ