ПРЕДИСЛОВИЕ

Компьютерный практикум по вероятностно-статистическим расчетам выполняют студенты

Пособие включает восемь четырехчасовых работ и задания по курсовому проекту.

ЛАБОРАТОРНАЯ РАБОТА №1. ВЕРОЯТНОСТНЫЕ РАСПРЕДЕЛЕНИЯ

1.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Нормальным распределением (или законом Гаусса) называется распределение непрерывной случайной величины Х, плотность которой определяется по формуле

где m и – параметры распределения. Можно доказать, что параметр m равен математическому ожиданию, а параметр – стандартному отклонению случайной величины Х.

Функция (интегральная) нормального распределения

Для краткой записи нормального распределения с параметрами m и используют обозначение N (m, ).

В частном случае параметры m = 0, = 1. Нормальное распределение N (0, 1) называется стандартным нормальным распределением. В этом случае плотность распределения

Функция стандартного нормального распределения иногда называется функцией Лапласа, она имеет специальное обозначение

Для вычисления значений плотности и функции нормального распределения в Excel используется встроенная статистическая функция НОРМРАСП.

Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.

Синтаксис:

НОРМРАСП(x;среднее;стандартное_откл;интегральная)

где x  — значение, для которого строится распределение.

Среднее  — среднее арифметическое распределения.

Стандартное_откл  — стандартное отклонение распределения.

Интегральная  — логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.

Замечания:

Если аргумент «среднее» или «стандартное_откл» не является числом, функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!.

Если стандартное_откл  ≤  0, то функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!.

Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.

Рис. 1.1

Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет вид (1.1)

Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x (1.2).

Пример 1.1.

1 2 3 4

A B Данные Описание 42 Значение, для которого требуется найти распределение 40 Среднее арифметическое распределения 1,5 Стандартное отклонение распределения Формула Описание (результат) =НОРМРАСП(A2;A3;A4;ИСТИНА) Функция интегрального распределения для приведенных выше условий (0,908789) =НОРМРАСП(A2;A3;A4;ЛОЖЬ) Функция плотности распределения (0,10934005)

ЗАДАНИЕ

1. Введите в таблицу значения аргумента х в диапазоне от –3 до 5 с шагом 0,2

2. Вычислите значение плотности стандартного нормального распределения, а также плотности нормального распределения с параметрами

m = 2, = 1; m = 0, = 0,5; m = 1, = 2.

3. Используя мастер диаграмм, постройте соответствующие кривые распределения (диаграмма ХУ, только линии, сглаживание линий).

4. Отредактируйте графики в соответствии с образцом оформления (рис.1.2).

5. Для заданных параметров нормального распределения постройте семейство графиков функции распределения.

Рис. 1.2. Образец оформления рабочего листа «Нормальное распределение»

1.2. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Экспоненциальным (или показательным) называется распределение непрерывной случайной величины Х, плотность которой

при х > 0 (при х 0 f(x) = 0).

Функция экспоненциального распределения

Математическое ожидание случайной величины Х, имеющей экспоненциальное распределение, равно

а дисперсия

Для вычисления значений плотности и функции экспоненциального распределения в Excel используется встроенная статистическая функция ЭКСПРАСП (рис. 1.3).

Возвращает экспоненциальное распределение. Функция ЭКСПРАСП используется для моделирования временных задержек между событиями, например времени, которое потребуется на доставку денежного перевода через автоматизированную банковскую систему. В частности, при помощи функции ЭКСПРАСП можно определить вероятности того, что этот процесс займет не более 1 минуты.

Синтаксис:

ЭКСПРАСП(x;лямбда ;интегральная)

где x  — значение функции.

Лямбда  — значение параметра.

Интегральная  — логическое значение, указывающее форму экспоненциальной функции, которую следует использовать. Если аргумент «интегральная» имеет значение ИСТИНА, функция ЭКСПРАСП возвращает интегральную функцию распределения; если имеет значение ЛОЖЬ, возвращается функция плотности распределения.

Замечания:

Если x или «лямбда» не является числом, функция ЭКСПРАСП возвращает значение ошибки #ЗНАЧ!.

Если x < 0, функция ЭКСПРАСП возвращает значение ошибки #ЧИСЛО!.

Если лямбда ≤ 0, функция ЭКСПРАСП возвращает значение ошибки #ЧИСЛО!.

Уравнение для функции плотности вероятности имеет вид (1.5).

Уравнение для интегральной функции распределения имеет вид (1.6).

Рис. 1.3. Встроенная функция ЭКСПРАСП

ЗАДАНИЕ

1. Введите в таблицу значения аргумента х в диапазоне от 0 до 20 с шагом 0,5.

2. Вычислите значение плотности экспоненциального распределения при = 1; =0,5; = 0,1.

3. Используя мастер диаграмм, постройте соответствующие кривые распределения (диаграмма ХУ, только линии, сглаживание линий).

4. Отредактируйте графики в соответствии с образцом оформления (рис.1.4).

5. Для заданных значений параметра постройте семейство графиков функции экспоненциального распределения.

Пример 1.2:

1 2 3

A B Данные Описание 0,2 Значение функции 10 Значение параметра Формула Описание (результат) =ЭКСПРАСП(A2;A3;ЛОЖЬ) Интегральная функция распределения (0,864665) =ЭКСПРАСП(0,2;10;ЛОЖЬ) Функция плотности распределения (1,353353)

Рис. 1.4. Образец оформления рабочего листа «Экспоненциальное распределение»

1.3. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Пусть проводится эксперимент, в результате которого нас интересует, произошло событие А или не произошло. Случай, в котором событие А произошло, назовем успехом, вероятность этого события . Если же событие А не произошло, то его вероятность .

Предположим теперь, что серия независимых испытаний такого типа проводится n раз. Нас интересует вероятность события, состоящего в том, что успех произошел ровно m раз, или вероятность того, что дискретная случайная величина Х, равная числу успехов, примет значение m. Решение этой задачи имеет вид:

где

– число сочетаний из n элементов по m. Формула (1.9) и задает биномиальный закон распределения дискретной случайной величины Х (в ее правой части – разложение бинома ).

Математическое ожидание случайной величины Х, имеющей биномиальное распределение, равно

а дисперсия

Для вычисления значений биномиального распределения в Excel используется встроенная статистическая функция БИНОМРАСП (рис. 1.5).

Возвращает отдельное значение биномиального распределения. Функция БИНОМРАСП используется в задачах с фиксированным числом тестов или испытаний, когда результатом любого испытания может быть только успех или неудача, испытания независимы, а вероятность успеха одинакова на протяжении всего эксперимента. Например, при помощи БИНОМРАСП можно вычислить, с какой вероятностью двое из трех следующих новорожденных будут мальчиками.

Синтаксис:

БИНОМРАСП(число_успехов;число_испытаний;вероятность_успеха ;интегральная)

где Число_успехов   — количество успешных испытаний.

Число_испытаний   — число независимых испытаний.

Вероятность_успеха   — вероятность успеха каждого испытания.

Интегральная   — логическое значение, определяющее вид функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция БИНОМРАСП возвращает интегральную функцию распределения, то есть вероятность того, что число успешных испытаний не меньше значения аргумента «число_успехов»; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция вероятностной меры, то есть вероятность того, что число успешных испытаний равно значению аргумента «число_успехов».

Замечания:

Число_успехов и число_испытаний усекаются до целых.

Если число_успехов, число_испытаний или вероятность_успеха не является числом, функция БИНОМРАСП возвращает значение ошибки #ЗНАЧ!.

Если число_успехов < 0 или число_успехов > число_испытаний, функция БИНОМРАСП возвращает значение ошибки #ЧИСЛО!.

Если вероятность_успеха < 0 или вероятность_успеха > 1, функция БИНОМРАСП возвращает значение ошибки #ЧИСЛО!.

Рис. 1.5. Встроенная функция БИНОМРАСП

Биномиальная функция распределения имеет вид:

Интегральное биномиальное распределение имеет вид:

Пример 1.3

1 2 3 4

A B Данные Описание 6 Количество успешных испытаний 10 Число независимых испытаний 0,5 Вероятность успеха в каждом испытании Формула Описание (результат) =БИНОМРАСП(A2;A3;A4;ЛОЖЬ) Вероятность того, что ровно 6 испытаний из 10 будут успешными (0,205078)

ЗАДАНИЕ

1. Введите в таблицу значения аргумента х в диапазоне от 0 до 25 с шагом 1.

2. Вычислите вероятности того, что успех в серии из 25 испытаний произойдет ровно х раз (х от 0 до 25) при вероятности успеха р = 0,7; р = 0,5; р = 0,2.

3. Используя мастер диаграмм, постройте соответствующие графики распределения (гистограмма, первый столбец как надпись).

4. Отредактируйте графики в соответствии с образцом оформления (рис.1.6).

Рис. 1.6. Образец оформления рабочего листа «Биномиальное распределение»

1.4. РАСПРЕДЕЛЕНИЕ ПУАССОНА

Пусть в условиях биномиального распределения число испытаний n велико, а вероятность успеха р мала. Если при этом np = 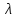= const, то можно показать, что (при )

Дискретная случайная величина Х имеет распределение Пуассона с параметром , если

где параметр = np > 0. Учитывая, что вероятность р мала, распределение Пуассона часто интерпретируют как закон редких явлений.

Математическое ожидание и дисперсия случайной величины Х, имеющей распределение Пуассона, одинаковы и равны параметру :

= = . (1.14)

Для вычисления значений распределения Пуассона в Excel используется встроенная статистическая функция ПУАССОН (рис. 1.7).

Возвращает распределение Пуассона. Обычное применение распределения Пуассона состоит в предсказании количества событий, происходящих за определенное время, например количества машин, появляющихся на площади за одну минуту.

Синтаксис:

ПУАССОН(x;среднее;интегральная)

где x  — количество событий.

Среднее  — ожидаемое численное значение.

Интегральная  — логическое значение, определяющее форму возвращаемого распределения вероятностей. Если аргумент «интегральная» имеет значение ИСТИНА, то функция ПУАССОН возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до x включительно. Если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения Пуассона, то есть вероятность точного равенства числа произошедших событий значению x.

Замечания:

Если x не является целым числом, оно усекается.

Если x или среднее не является числом, то функция ПУАССОН возвращает значение ошибки #ЗНАЧ!.

Если x < 0, то функция ПУАССОН возвращает значение ошибки #ЧИСЛО!.

Если среднее ≤ 0, то функция ПУАССОН возвращает значение ошибки #ЧИСЛО!.

Функция ПУАССОН вычисляется следующим образом.

Если интегральная = ЛОЖЬ:

Рис. 1.7. Встроенная функция POISSON Если интегральная = ИСТИНА:

ЗАДАНИЕ

1. Введите в таблицу значения аргумента х в диапазоне от 0 до 40 с шагом 1.

2. Вычислите вероятности того, что успех в серии из 40 испытаний произойдет ровно х раз (х от 0 до 40) при λ = 10; λ = 20; λ = 30.

3. Используя мастер диаграмм, постройте соответствующие графики распределения (гистограмма, первый столбец как надпись).

4. Отредактируйте графики в соответствии с образцом оформления (рис.1.8).

Пример 1.4:

1 2 3

A B Данные Описание 2 Число событий 5 Ожидаемое среднее Формула Описание (результат) =ПУАССОН(A2;A3;ИСТИНА) Интегральное распределение Пуассона для приведенных выше условий (0,124652) =ПУАССОН(A2;A3;ЛОЖЬ) Функция плотности распределения Пуассона для приведенных выше условий (0,084224)

Рис. 1.8. Образец оформления рабочего листа «Распределение Пуассона»

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Вычислить значение функции нормального распределения с математическим ожиданием 12 и стандартным отклонением 2 при х = 8.

2. Построить кривую нормального распределения с математическим ожиданием 12 и стандартным отклонением 2.

3. Построить кривую экспоненциального распределения с параметром = 0,001.

4. Какова вероятность, что при 10 подбрасываниях монеты герб выпадет ровно два раза? Воспользоваться встроенной функцией биномиального распределения.

5. Предприятие отпустило поставщику партию из 1000 изделий. Вероятность повреждения в пути составляет 0,002. Какова вероятность, что поставщик получит пять изделий дефектными? Воспользоваться встроенной функцией распределения Пуассона.

6. Во многих статистических расчетах используется бета-распределение. Ознакомиться по справке с встроенной функцией БЕТАРАСП.

7. Вычислить значение плотности бета-распределения с параметрами =5 и =3 при х=6,

где – Степени_свободы1; - Степени_свободы2.

8. В условиях предыдущего примера построить кривую бета-распределения.

ЛАБОРАТОРНАЯ РАБОТА №2. ОПИСАТЕЛЬНАЯ СТАТИСТИКА

2.1. ПОСТРОЕНИЕ ГИСТОГРАММ

Результаты наблюдений в выборке записываются в порядке их регистрации - объем выборки. Вариационным называется ряд, составленный из элементов выборки в порядке их возрастания: . При этом минимальный элемент выборки , максимальный элемент . Разность между максимальным и минимальным элементами выборки называется размахом:

. (2.1)

При достаточно большом объеме выборки данные группируют – разбивают на интервалы, как правило, одинаковой длины. Количество интервалов k выбирается в зависимости от объема выборки, обычно от 8 до 20 интервалов. Иногда используется эмпирическая формула

k = 1 + 3,32 lg n. (2.2)

Ширина интервала

w = R / k. (2.3)

Количество элементов выборки, попавших в i-й интервал (i = 1, 2, …, k), называется частотой. Результаты расчета сводят в таблицу частот, в которой показывают границы интервалов, середины каждого интервала, частоты, относительные частоты , накопленные относи-

тельные частоты , а также относительные частоты, деленные на длину интервала . Эти данные используются для графического представления выборки.

Выборочным распределением называется распределение дискретной случайной величины, принимающей значения с вероятностями . График выборочной функции распределения F*(x) строится по значениям накопленных относительных частот. Можно показать, что при большом объеме выборки выборочная функция распределения является приближенной оценкой функции распределения F(x) генеральной совокупности.

Гистограмма частот строится по значениям и является приближенной оценкой плотности распределения f(x) генеральной совокупности. Часто для простоты на гистограмме откладывают значения абсолютных частот . При этом меняется только масштаб по оси ординат.

Гистограмма позволяет визуально представить характер распределения изучаемой величины: оценить его симметричность, положение центра, рассеяние, проверить, является ли распределение унимодальным или имеется несколько вершин, сравнить положение центра распределения с требуемым математическим ожиданием (если оно задано), а рассеяние с границами допуска.

При анализе характера распределения иногда полезна стратификация данных. Если одно и то же изделие изготавливается разными рабочими, часто имеет смысл проанализировать работу каждого из них отдельно: провести стратификацию, или расслоение, по квалификации рабочих. При использовании материала из разных партий иногда уточнить природу дефекта можно, если анализировать эти партии раздельно.

В производстве для стратификации удобен метод, называемый 5М (по первым буквам английских наименований): необходимо провести стратификацию данных по квалификации работников (men), по используемому оборудованию (machine), по материалам (material), по технологии изготовления (method), по методам и средствам измерения (measure).

Для построения гистограммы в Excel необходимо ввести в таблицу результаты наблюдений и подготовить столбец рассчитанных значений границ интервалов. Для подсчета частот используется функция массива ЧАСТОТА (рис. 2.1), которая возвращает частотное распределение в виде массива из одного столбца. Функция служит для подсчета количества значений в массиве данных, которые находятся в значениях, заданных исходным массивом.

Вычисляет частоту появления значений в интервале значений и возвращает массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, она должна задаваться в качестве формулы массива.

Синтаксис:

ЧАСТОТА(массив_данных;массив_интервалов)

где Массив_данных  — массив или ссылка на множество данных, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.

Массив_интервалов  — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».

Рис. 2.1. Встроенная функция массива ЧАСТОТА

Пример 2.1.

1 2 3 4 5 6 7 8 9 10

A B Баллы Интервалы 79 70 85 79 78 89 85 50 81 95 88 97 Формула Описание (результат) =ЧАСТОТА(A2:A10;B2:B4) Число баллов меньше или равно 70 (1) Число баллов в интервале 71-79 (2) Число баллов в интервале 80-89 (4) Число баллов больше или равно 90 (2)

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон A13:A16, нажмите клавишу F2, а затем нажмите клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке A12 (1).

Замечания:

Функция ЧАСТОТА вводится как формула массива после выделения интервала смежных ячеек, в которые требуется вернуть полученный массив распределения.

Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.

Функция ЧАСТОТА игнорирует пустые ячейки и текст.

Формулы, возвращающие массивы, должны быть введены как формулы массива.

ЗАДАНИЕ

1. Введите в один столбец результаты измерений, выполненных на двух станках А и Б:

2. Найдите максимальное и минимальное значения, используя встроенные статистические функции MAX и MIN.

3. Вычислите размах выборки.

4. Найдите ширину интервала, если требуется разбить выборочные данные на 8 интервалов.

5. Подготовьте массив классов: в качестве первого значения введите найденное минимальное значение, последующие значения – с шагом, равным ширине интервала.

6. Вычислите частоты, используя функцию массива ЧАСТОТА.

7. С помощью мастера диаграмм постройте гистограмму частот.

8. Отредактируйте графики в соответствии с образцом оформления (рис. 2.2).

9. Стратифицируйте гистограмму по станкам: проведите расчеты по пунктам 2 – 8 отдельно для станка А и для станка Б.

10. Сформулируйте выводы по результатам рассмотрения трех построенных гистограмм.

2.2. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ВЫБОРКИ

Выборочное среднее (математическое ожидание выборки)

Выборочная мода Mo*– элемент выборки, встречающийся с наибольшей частотой (для унимодального – одновершинного распределения).

Выборочная медиана Me* – число, которое делит вариационный ряд на две части, содержащие одинаковое количество элементов; если объем выборки нечетен n = 2t + 1, то Me* =; при n = 2t Me* =

Рис. 2.2. Образец оформления рабочего листа «Гистограмма»

Выборочная дисперсия

Несмещенная дисперсия

Выборочное стандартное отклонение

или

Выборочный коэффициент асимметрии

(здесь – выборочный центральный момент k-го порядка);

выборочный коэффициент эксцесса

Для вычисления значений этих характеристик в Excel используются встроенные статистические функции:

1. СРЗНАЧ – среднее значение по формуле (2.4),

2. МОДА – мода,

3. МЕДИАНА – медиана,

4. ДИСПР – дисперсия (2.5),

5. ДИСП – дисперсия (2.6),

6. СТАНДОТКЛОНП – стандартное отклонение (2.7),

7. СТАНДОТКЛОН – стандартное отклонение (2.8),

8. СКОС – коэффициент асимметрии (2.9),

9. ЭКСЦЕСС – коэффициент эксцесса (2.10).

Синтаксис этих функций практически одинаков. Например, функция СРЗНАЧ возвращает среднее арифметическое своих аргументов:

Синтаксис

СРЗНАЧ(число1; число2; ...)

Число1, число2, ...   — от 1 до 255 аргументов, для которых вычисляется среднее.

Замечания:

Аргументы могут быть либо числами, либо именами, массивами или ссылками, содержащими числа.

Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.

Аргументы, являющиеся значениями ошибок или текстом, которые не могут быть преобразованы в числа, вызывают ошибки.

Если логические значения и

Рис. 2.3. Встроенная статистическая функция СРЗНАЧ текстовые представления чисел необходимо включить в ссылку в качестве части расчета, используйте функцию СРЗНАЧА.

 Примечания.    

1) Функция СРЗНАЧА оценивает степень централизации данных — расположение центра группы чисел в статистическом распределении. Существует три способа оценки степени централизации:

Среднее значение   — это среднее арифметическое, рассчитанное путем сложения группы чисел и деления на количество этих чисел. Например, среднее арифметическое 2, 3, 3, 5, 7 и 10 находится путем деления 30 на 6, что дает в результате 5.

2) МОДА возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных, т.е. это число, которое встречается наиболее часто в группе чисел. Например, мода для 2, 3, 3, 5, 7 и 10 — 3. Функция МОДА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении.

3) Медиана   — возвращает медиану заданных чисел, т.е. это число, которое находится в середине группы, является серединой множества чисел; значения половины чисел в группе чисел больше медианы, значения другой половины — меньше. Например, медиана для группы чисел 2, 3, 3, 5, 7 и 10 — 4. Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении.

При симметричном распределении множества чисел эти величины оценки степени централизации равны. При ассиметричном распределении множества чисел они могут отличаться.

Совет:  Вычисляя средние значения ячеек, следует учитывать различие между пустыми ячейками и ячейками, содержащими нулевые значения, особенно если не установлен флажок

4) В функции ДИСП, которая оценивает дисперсию по выборке, предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.

5) Функция СТАНДОТКЛОН оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего. Эта функция предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП. Стандартное отклонение вычисляется с использованием «n-1» метода.

6) Функция ЭКСЦЕСС возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

7) Функция СКОС возвращает асимметрию распределения. Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.

Пример 2.2

1 2 3 4 5 6

A Данные 10 7 9 27 2 Формула Описание (результат) =СРЗНАЧ(A2:A6) Среднее арифметическое приведенных выше чисел (11) =СРЗНАЧ(A2:A6; 5) Среднее арифметическое приведенных выше чисел и числа 5 (5)

Рис. 2.3. Встроенная статистическая функция СРЗНАЧ

ЗАДАНИЕ

Определите числовые характеристики для всей выборки из предыдущего задания, затем отдельно – для станков А и Б (на рис. 2.2 показаны результаты расчета только для станка А).

2.3. ДИАГРАММА ПАРЕТО

Диаграмма Парето в задачах управления качеством предназначена для выявления причин появления немногочисленных существенно важных дефектов; часто можно устранить почти все потери, сосредоточив усилия на ликвидации именно этих причин и отложив пока рассмотрение причин, приводящих к остальным многочисленным, но не слишком существенным дефектам. Это следует из принципа Парето, который применительно к вопросам дефектности изделий может быть сформулирован так: подавляющее число дефектов и связанных с ними потерь (примерно 80 %) возникает из-за относительно небольшого числа причин (20 %).

Диаграмма Парето по результатам деятельности отражает дефекты, рекламации, срывы сроков поставок, несчастные случаи и т. п.

Диаграмма Парето по причинам проблем, возникающих в ходе производства, используется для выявления наиболее важной из них: квалификации рабочего, качества оборудования, вида сырья, поставщика, условий производства и т.п.

Для построения диаграммы вначале надо выяснить, какую проблему необходимо исследовать, какие данные надо собрать, как эти данные классифицировать. Готовится и заполняется контрольный листок, на его основе оформляется бланк для построения диаграммы, в котором факторы сортируются в порядке убывания их значимости (кроме фактора «Прочие», который вводится в последнюю очередь), вычисляются накопленное количество дефектов и соответствующий накопленный процент.

На графике показывается как абсолютные значения в виде столбиковой диаграммы, так и накопленный процент в виде ломаной линии.

ЗАДАНИЕ

По результатам приемочного контроля штампованных деталей получены данные о дефектах (таблица); построить диаграмму Парето (рис. 2.4).

Дефект	Деформация	Вмятина	Скол	Заусенец	Раковина	Царапина	Трещина	Прочие
Всего	68	46	9	8	4	3	1	2

Рис. 2.4. Образец оформления рабочего листа «Диаграмма Парето»

Из диаграммы Парето по рис. 2.4 видим, что 81% дефектов – это деформации и вмятины. Именно на устранение этих дефектов необходимо обратить особое внимание. Следующим шагом может стать анализ причин дефектов с использованием соответствующих диаграмм Парето.

2.4. ДИАГРАММА РАССЕЯНИЯ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Диаграмма рассеяния предназначена для изучения связи между двумя показателями. Пусть, например, исследуется связь между рекламациями по деталям А и В: за первый период наблюдения получено рекламаций по детали А и рекламаций по детали В, за второй – соответственно и , и т. д. Откладывая соответствующие значения в системе координат (х,у), получим диаграмму рассеяния. По диаграмме рассеяния можно визуально оценить наличие связи между двумя показателями, характер этой связи (положительная или отрицательная), степень ее тесноты.

Для количественного анализа степени тесноты связи между двумя случайными величинами Х и Y вводится специальная характеристика, называемая ковариацией:

где и – соответственно математические ожидания величин Х и Y.

Отношение ковариации к произведению стандартных отклонений называется коэффициентом корреляции:

Коэффициент корреляции не превышает по модулю единицы и характеризует степень тесноты линейной связи между переменными Х и Y. При > 0 корреляция называется положительной: с увеличением значений Х в среднем происходит и рост значений Y, при < 0 – отрицательной. Если = 0 случайные величины Х и Y называются некоррелированными; это не означает, что эти величины не связаны между собой, но линейной связи между ними нет. При | | = 1 переменные Х и Y связаны функциональной зависимостью вида .

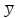Пусть , – двумерная выборка объема n из наблюдений за случайными величинами Х и Y (i = 1, 2, …, n). Учитывая, что для выборки аналогом математического ожидания являются выборочные средние и , получим из формулы (2.11) зависимость для расчета выборочной ковариации:

а из формулы (2.12) – зависимость для расчета выборочного коэффициента корреляции

Для вычисления коэффициента корреляции в Excel используется встроенная статистическая функция КОРРЕЛ (рис. 2.5).

Функция КОРРЕЛ возвращает коэффициент корреляции между интервалами ячеек «массив1» и «массив2». Коэффициент корреляции используется для определения взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера.

Синтаксис

КОРРЕЛ(массив1;массив2)

здесь Массив1   — это интервал ячеек со значениями.

Массив2   — второй интервал ячеек со значениями.

Замечания:

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.

Если массив1 и массив2 имеют различное количество точек данных, то функция КОРРЕЛ возвращает значение ошибки #Н/Д.

Если какой-либо из массивов пуст или если σ (стандартное отклонение) их значений равняется нулю, функция КОРРЕЛ возвращает значение ошибки #ДЕЛ/0!.

Уравнение для коэффициента Рис. 2.5. Встроенная статистическая функция КОРРЕЛ корреляции имеет следующий вид:

где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Пример 2.3

1 2 3 4 5 6

A B Данные1 Данные2 3 9 2 7 4 12 5 15 6 17 Формула Описание (результат) =КОРРЕЛ(A2:A6;B2:B6) Коэффициент корреляции между двумя массивами приведенных выше данных (0,997054)

ЗАДАНИЕ

1. В таблице представлены результаты исследования зависимости времени оформления документа, y (мин.) от количества специалистов в офисе х:

x	1	2	3	4	5	6	7
y	6	4	2	2	1,5	1	1

Построить диаграмму рассеяния, вычислить коэффициент корреляции.

2. Проанализировать степень тесноты связи между количеством дефектов в узлах А (х) и В (y) для двух цехов, где изготавливаются эти узлы.

x	1	2	4	1	6	7	2	4	3	5	7	7	7
y	3	2	2	2	1	0	4	3	5	4	3	2	4
цех	1	1	1	1	1	1	2	2	2	2	2	2	2

Построить диаграммы рассеяния и найти коэффициенты корреляции для всей совокупности данных, а также отдельно для цеха 1 и цеха 2.

2.5. КВАНТИЛИ РАСПРЕДЕЛЕНИЙ

При построении доверительных интервалов, проверке гипотез и в других статистических расчетах используются квантили некоторых распределений.

Квантилью порядка р называется число , для которого функция распределения F(x) принимает значение р:

Для определения квантилей наиболее важных распределений в Excel используются встроенные статистические функции.

1) Квантили стандартного нормального распределения порядка р (рис. 2.6):

НОРМСТОБР – возвращает обратное значение стандартного нормального распределения. Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице.

Синтаксис

НОРМСТОБР(вероятность)

Здесь Вероятность  — вероятность, соответствующая нормальному распределению.

Рис. 2.6. Вычисление квантили нормального распределения u0,908

Замечания:

Если значение аргумента «вероятность» не является числом, функция НОРМСТОБР возвращает значение ошибки #ЗНАЧ!.

Если вероятность < 0 или вероятность > 1, то функция НОРМОБР возвращает значение ошибки #ЧИСЛО!.

Для заданного значения вероятности функция НОРМСТОБР находит значение z, при котором НОРМСТРАСП(z) = вероятность. Таким образом, точность функции НОРМСТОБР зависит от точности функции НОРМСТРАСП. В функции НОРМСТОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает значение ошибки #Н/Д.

Пример 2.4

.

1 2	A B Формула Описание (результат) =НОРМСТОБР(0,908789) Обратное значение стандартного нормального распределения с вероятностью 0,908789 (1,3333)

2) Квантиль распределения хи-квадрат с k степенями свободы порядка р (рис. 2.7): 30

ХИ2ОБР – возвращает значение, обратное односторонней вероятности распределения хи-квадрат. Если вероятность = ХИ2РАСП(x;...), то ХИ2ОБР(вероятность;...) = x. Данная функция позволяет сравнить наблюдаемые результаты с ожидаемыми, чтобы определить, была ли верна исходная гипотеза.

Синтаксис

ХИ2ОБР(вероятность;степени_свободы)

здесь Вероятность  — вероятность, связанная с распределением c2 (хи-квадрат).

Степени_свободы  — число степеней свободы.

Заметки:

Если какой-либо из аргументов не является числом, функция ХИ2ОБР возвращает значение ошибки #ЗНАЧ!.

Если вероятность < 0 или вероятность > 1, функция ХИ2ОБР возвращает значение ошибки #ЧИСЛО!.

Если значение аргумента «степени_свободы» не является целым числом, оно усекается.

Рис. 2.7. Вычисление квантили распределения хи-квадрат

Если степени_свободы  <  1 или степени_свободы  ≥  10^10, ХИ2ОБР возвращает значение ошибки #ЧИСЛО!.

Если задано значение вероятности, то функция ХИ2ОБР ищет значение x, для которого функция ХИ2РАСП(x; степень_свободы) = вероятность. Однако точность функции ХИ2ОБР зависит от точности ХИ2РАСП. В функции ХИ2ОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает сообщение об ошибке #Н/Д.

Пример 2.5

1 2 3

A B Данные Описание 0,050001 Вероятность, связанная с распределением хи-квадрат 10 Степени свободы Формула Описание (результат) =ХИ2ОБР(A2;A3) Значение, обратное односторонней вероятности распределения хи-квадрат (18,3069735)

3) Квантиль t-распределения Стьюдента с k степенями свободы порядка р (рис. 2.8):

СТЬЮДРАСПОБР – возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы.

Синтаксис

СТЬЮДРАСПОБР(вероятность;степени_свободы)

здесь Вероятность  — вероятность, соответствующая двустороннему распределению Стьюдента.

Степени_свободы  — число степеней свободы, характеризующее распределение.

Рис. 2.8. Вычисление квантили распределения Стьюдента

Замечания:

Если любой из аргументов не является числом, то функция СТЬЮДРАСПОБР возвращает значение ошибки #ЗНАЧ!.

Если вероятность < 0 или вероятность > 1, то функция СТЬЮДРАСПОБР возвращает значение ошибки #ЧИСЛО!.

Если значение аргумента «степени_свободы» не является целым числом, оно усекается.

Если степени_свободы < 1, то функция СТЬЮДРАСПОБР возвращает значение ошибки #ЧИСЛО!.

Функция СТЬЮДРАСПОБР возвращает значение t, для которого P(|X| > t) = вероятность, где X — случайная величина, соответствующая t-распределению, и P(|X| > t) = P(X < -t или X > t).

Одностороннее t-значение может быть получено при замене аргумента «вероятность» на 2*вероятность. Для вероятности 0,05 и 10 степеней свободы двустороннее значение вычисляется по формуле СТЬЮДРАСПОБР(0,05;10) и равно 2,28139. Одностороннее значение для той же вероятности и числа степеней свободы может быть вычислено по формуле СТЬЮДРАСПОБР(2*0,05;10), возвращающей значение 1,812462.

 Примечание.     В некоторых таблицах вероятность описана как (1-p).

Если задано значение вероятности, то функция СТЬЮДРАСПОБР ищет значение x, для которого функция СТЬЮДРАСП(x, степени_свободы, 2) = вероятность. Однако точность функции СТЬЮДРАСПОБР зависит от точности СТЬЮДРАСП. В функции СТЬЮДРАСПОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает значение ошибки #Н/Д.

Пример 2.6

1 2 3

А B Данные Описание 0,054644927 Вероятность, соответствующая двустороннему распределению Стьюдента. 60 Степени свободы Формула Описание (результат) =СТЬЮДРАСПОБР(A2;A3) T-значение распределения Стьюдента для приведенных выше условий (1,959999998)

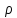Квантили распределения Стьюдента используются, в частности, при проверке значимости корреляции. Пусть r – выборочный коэффициент корреляции, вычисленный по выборке объема n из генеральной совокупности, имеющей нормальное распределение. Требуется на заданном уровне значимости  проверить нулевую гипотезу о равенстве нулю коэффициента корреляции для генеральной совокупности Н0: = 0.

Если нулевая гипотеза будет отвергнута, то говорят о значимости коэффициента корреляции, то есть о наличии корреляции между X и Y. Если же нулевая гипотеза принимается, то корреляция незначима: X и Y некоррелированы (несмотря на то, что выборочный коэффициент корреляции ).

Для проверки рассматриваемой гипотезы используется статистика

имеющая распределение Стьюдента с числом степеней свободы (n – 2).

Пусть, например, альтернативная гипотеза Н₁: < 0 (левосторонний критерий), тогда граница критической области определяется квантилью ; если же Н₁: определяются границы двухсторонней критической области и

4) Квантиль F-распределения Фишера с числами степеней свободы k1 в числителе и k1 в знаменателе порядка р (рис. 2.9):

ФИШЕРОБР – обратное преобразование Фишера. Это преобразование используется при анализе корреляции между массивами или интервалами данных. Если y = ФИШЕР(x), то ФИШЕРОБР(y) = x.

Синтаксис:

ФИШЕРОБР(y)

здесь y  — значение, для которого производится обратное преобразование.

Рис. 2.9. Вычисление квантили распределения Фишера

Замечания:

Если «y» не является числом, функция ФИШЕРОБР возвращает значение ошибки #ЗНАЧ!.

Уравнение для обратного преобразования Фишера имеет следующий вид:

Пример 2.7

1 2	A B Формула Описание (результат) =ФИШЕРОБР(0,972955) Обратное преобразование Фишера для аргумента 0,972955 (0,75)

ЗАДАНИЕ

1. Используя встроенные статистические функции найти квантили

,

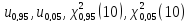Проверить найденные значения по таблицам квантилей.

2. Проверить значимость корреляции в первом примере предыдущего за-

дания, используя односторонний критерий на уровне значимости 0,05.

(оформить расчет в соответствии с рис. 2.10).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дана выборка: 2, 3, 5, 4, 3, 2, 2, 1, 3, 5, 2, 3, 4,3, 3. Построить гистограмму частот, разбив данные на пять интервалов.

2. Для выборки из предыдущей задачи найти среднее значение, несмещенную дисперсию и стандартное отклонение, асимметрию, эксцесс.

3. В качестве характеристики центра иногда используется среднее геометрическое. Ознакомиться с встроенной функцией GEOMEAN по справке и вычислить ее значение для выборки из задачи 1.

4. Анализировались способы поступления жалоб на работу магазина за определенное время. По результатам, приведенным в таблице, построить диаграмму Парето. Сделать выводы.

№	Способ поступления жалобы	Количество жалоб
1	Запись в книге жалоб	11
2	По обычной почте	2
3	По электронной почте	4
4	Обратились лично	3
5	Жалоба на сайте фирмы	15
6	Письменное заявление	2

5. Определить квантили распределений:

,

6. Дана двумерная выборка. Построить диаграмму рассеяния, вычислить коэффициент корреляции, проверить значимость.

x	2	8	6	5	3	2
y	5	12	8	7	4	6

Рис. 2.10. Образец оформления рабочего листа «Диаграмма рассеяния»

ЛАБОРАТОРНАЯ РАБОТА №3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

3.1. ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ СРЕДНЕГО ЗАДАННОМУ ЗНАЧЕНИЮ

Общая последовательность проверки гипотезы о параметрах распределения такова:

- формулируются нулевая и альтернативная гипотезы H₀ и H₁;

- задается уровень значимости ;

- выбирается статистика Z для проверки гипотезы H₀;

- определяется выборочное распределение статистики Z;

- в зависимости от вида альтернативной гипотезы и распределения статистики Z определяется граница критической области;

- вычисляется выборочное значение z_в статистики Z;

- принимается статистическое решение: если выборочное значение статистики z_в оказывается в области принятия решения, гипотеза H₀ принимается; в противном случае гипотеза H₀ отклоняется, как несогласующаяся с результатами наблюдений.

Предположим, что проверяется гипотеза о средней нормально распределенной генеральной совокупности при известной дисперсии , то есть . Нетрудно показать, что статистикой критерия может служить величина

распределенная по закону N(0,1).

Если же дисперсия неизвестна, то используется статистика

имеющая распределение Стъюдента с (n – 1) степенью свободы.

Задачи такого типа в Excel можно решать двояко. Во-первых, может быть использован описанный стандартный алгоритм: по опытным данным вычисляется выборочное значение соответствующей статистики и сравнивается с критическим; при попадании выборочного значения в критическую область гипотеза отвергается. Этот алгоритм, в частности, уже был использован при проверке значимости корреляции в предыдущем задании.

Во-вторых, для проверки некоторых гипотез в Excel есть специальные встроенные функции. Так, для проверки гипотезы о равенстве среднего заданному значению может быть использована функция ZTECT - вычисляет двухстороннюю вероятность значений z-теста при стандартном распределении (рис. 3.1).

Функция ZTECT возвращает одностороннее значение вероятности z-теста. Для заданного гипотетического среднего генеральной совокупности (μ0) функция ZTEСT возвращает вероятность того, что выборочное среднее будет больше среднего значения множества рассмотренных данных (массива), называемого также средним значением наблюдаемой выборки.

Синтаксис

ZТЕСТ(массив;μ0;сигма)

здесь Массив  — массив или диапазон данных, с которыми сравнивается μ0.

μ0   — проверяемое значение.

Сигма  — известное стандартное отклонение генеральной совокупности. Если этот аргумент опущен, используется стандартное отклонение выборки.

Замечания:

Если массив пуст, то функция ZТЕСТ возвращает значение ошибки #Н/Д.

Функция ZТЕСТ вычисляется следующим образом. Если аргумент «сигма» не опущен:

Если аргумент «сигма» опущен:

где x — выборочное среднее значение СРЗНАЧ(массив); s — выборочное среднеквадратичное отклонение СТАНДОТКЛОН(массив); n — число наблюдений СЧЕТ(массив).

Функция ZTEСT представляет вероятность того, что выборочное среднее будет больше среднего значения множества рассмотренных данных СРЗНАЧ(массив) при значении математического ожидания, равном μ0. Исходя из симметрии нормального распределения, если СРЗНАЧ(массив) < μ0, функция ZTEСT вернет значение больше 0,5.

Приведенную ниже формулу Microsoft Excel можно использовать для вычисления двустороннего значения вероятности того, что выборочное среднее будет отличаться от μ0 (в любом направлении) больше, чем СРЗАНЧ(массив), при математическом ожидании генеральной совокупности, равном μ0.

=2 * МИН(ZTEСT(массив;μ0;сигма), 1 - ZTEСT(массив;μ0;сигма)).

Пример 3.1

1 2 3 4 5 6 7 8 9 10 11

А Данные 3 6 7 8 6 5 4 2 1 9 Формула Описание (результат) =ZТЕСТ(A2:A11;4) Одностороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 4 (0,090574) =2 * МИН(ZТЕСТ(A2:A11;4); 1 - ZТЕСТ(A2:A11;4)) Двустороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 4 (0,181148) =ZТЕСТ(A2:A11;6) Одностороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 6 (0,863043) =2 * МИН(ZТЕСТ(A2:A11;6); 1 - ZТЕСТ(A2:A11;6)) Двустороннее значение вероятности z-теста для приведенного выше множества данных при гипотетическом математическом ожидании 6 (0,273913)

При использовании этой функции вычисляется вероятность того, что для генеральной совокупности справедлива гипотеза H0: m = m0. Используется двухсторонний критерий, то есть альтернативная гипотеза H1: m m0. Если эта вероятность меньше заданного уровня значимости, гипотеза отклоняется.

Рис. 3.1. Встроенная статистическая функция ZTEСT

ЗАДАНИЕ

Шарики, изготовленные станком-автоматом, должны иметь диаметр 10 мм; проверить эту гипотезу по заданной выборке на уровне значимости 0,05, если:

A) Дисперсия известна и равна 0,1 мм²,

B) Дисперсия неизвестна.

Результаты наблюдений приведены в таблице.

10,16	9,99	9,8	10,27	10,13	9,97	10,04	10,16	10,19	10,26
9,96	9,89	10,11	10,3	10,15	10,04	10,39	10,43	10,03	10,32

Воспользоваться стандартным алгоритмом проверки гипотез и встроенной функцией ZTEСT.

Оформление задания – в соответствии с рис. 3.2.

Рис. 3.2. Образец оформления рабочего листа при проверке гипотезы о среднем

3.2. ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ ДИСПЕРСИЙ

При проверке гипотеза о равенстве дисперсий двух нормально распределенных совокупностей при неизвестных математических ожиданиях m1 и m2 используется статистика

которая имеет F-распределение Фишера с числом степеней свободы (n₁ – 1) и (n₂ – 1); здесь n₁ и n₂ – объемы выборок, – соответствующие несмещенные дисперсии; при этом предполагается , что .

Для проверки этой гипотезы в Excel есть функция ФТЕСТ – возвращает результат F-теста (рис. 3.3).

Рис. 3.3 Встроенная статистическая функция FTEST

Функция ФТЕСТ возвращает результат F-теста. F-тест возвращает двустороннюю вероятность того, что разница между дисперсиями аргументов «массив1» и «массив2» несущественна. Эта функция позволяет определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, можно определить, имеют ли эти школы различные уровни разброса результатов тестирования.

Синтаксис:

ФТЕСТ(массив1;массив2)

здесь Массив1   — первый массив или интервал данных.

Массив2   — второй массив или интервал данных.

Пример 3.2

1 2 3 4 5 6

A B Данные1 Данные2 6 20 7 28 9 31 15 38 21 40 Формула Описание (результат) =ФТЕСТ(A2:A6;B2:B6) F-тест для приведенных выше данных (0,648318)

Замечания:

Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

Если количество точек данных в аргументе «массив1» либо «массив2» меньше 2 или если дисперсия аргумента «массив1» либо «массив2» имеет нулевое значение, функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!.

ЗАДАНИЕ

Проверить гипотезу об одинаковой точности работы станков по результатам измерений (точность характеризуется дисперсией соответствующего размера) на уровне значимости 0,05 с использованием формулы (3.3) и функции ФТЕСТ. Результаты измерений контролируемого параметра на двух станках приведены в таблице. Оформление расчетов – в соответствии с рис. 3.4.

№	Станок1	Станок2	№	Станок1	Станок2
1	12,05	12,36	13	12,05	12,47
2	12,08	12,45	14	12,08	12,41
3	12,33	12,48	15	12,33	12,34
4	12,34	12,56	16	12,05	12,51
5	12,75	12,63	17	12,08	12,45
6	12,32	12,25	18	12,31	12,24
7	12,12	12,54	19	12,34	12,55
8	12,05	12,35	20	12,42	12,32
9	12,08	12,54	21	12,42	12,44
10	12,33	12,33	22	12,12	12,41
11	12,08	12,85	23		12,38
12	12,75	12,42	24		12,51

Рис. 3.4. Образец оформления рабочего листа при проверке гипотезы о равенстве дисперсий

3.3.ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ СРЕДНИХ

Часто на практике возникает задача о сравнении средних двух нормально распределенных совокупностей, то есть о проверке гипотезы . Если соответствующие дисперсии и известны, то в качестве статистики принимается величина

распределенная по закону N(0,1).

Здесь – соответствующие выборочные средние,

n₁ и n₂ – объемы выборок.

Если же дисперсии генеральных совокупностей неизвестны, то используемая для проверки гипотезы статистика и ее распределение зависит от того, принимается ли гипотеза о равенстве дисперсий.

В случае принятия гипотезы о равенстве дисперсий используется статистика

где

Эта статистика имеет распределение t(n₁ + n₂ – 2).

При отклонении гипотезы о равенстве дисперсий применяется статистика

c распределением t(k), где

Для проверки этой гипотезы в Excel есть функция ТТЕСТ (рис. 3.5) – вычисляет t-тест (вероятность, ассоциированную с проверкой по критерию Стьюдента).

Функция ТТЕСТ возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ позволяет определить, вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Рис. 3.5. Встроенная статистическая функция ТTEST

Синтаксис:

ТТЕСТ(массив1;массив2;хвосты;тип)

здесь Массив1  — первое множество данных.

Массив2  — второе множество данных.

Хвосты  — число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение.

Тип  — вид выполняемого t-теста.

Тип	Выполняемый тест
1	Парный
2	Двухвыборочный с равными дисперсиями (гомоскедастический)
3	Двухвыборочный с неравными дисперсиями (гетероскедастический)

Замечания:

Если аргументы «массив1» и «массив2» имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д.

Аргументы «хвосты» и «тип» усекаются до целых значений.

Если аргумент «хвосты» или «тип» не является числом, то функция ТТЕСТ возвращает значение ошибки #ЗНАЧ!.

Если аргумент «хвосты» имеет значение, отличное от 1 и 2, то функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!.

Функция TTEСT использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если хвосты = 1, TTEСT возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией TTEСT в случае, когда хвосты = 2, вдвое больше значения, возвращаемого, когда хвосты = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими генеральной совокупности с одним и тем же средним.

Пример 3.3

1 2 3 4 5 6 7 8 9 10

А B Данные 1 Данные 2 3 6 4 19 5 3 8 2 9 14 1 4 2 5 4 17 5 1 Формула Описание (результат) =ТТЕСТ(A2:A10;B2:B10;2;1) Вероятность, соответствующая парному критерию Стьюдента, с двусторонним распределением (0,196016)

ЗАДАНИЕ

1. В предыдущей задаче о точности станков проверить гипотезу о равенстве средних значений, используя t-тест; при вводе параметров t-теста учесть, что гипотеза о равенстве дисперсий была отклонена; данные считать с рабочего листа с проверкой равенства дисперсий;

2. Используя F-тест и t-тест, решить задачу:

Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12.00 до 13.00. На протяжении недели записывалось время ожидания клиентов (количество минут от момента входа в банк до момента начала обслуживания). Получена выборка 4,21; 5,55; 3,02; 5,13; 4,77; 2,34; 3,54; 3,20; 4,50; 6,10; 0,38; 5,12. Другой филиал банка, расположенный в жилом районе, обеспокоен обслуживанием клиентов в конце недели, в пятницу с 17.00 до 19.00. Получены следующие данные: 9,66; 5,90; 8,02; 5,79; 8,73; 3,82; 8,01; 8,35; 0,49; 6,68; 5,64; 4,08; 6,17; 9,91; 5,47. Есть ли основание утверждать, что оба филиала имеют одинаковое среднее время ожидания клиентов?

Оформить рабочий лист в соответствии с рис. 3.6.

Рис. 3.6. Образец оформления рабочего листа при проверке гипотезы о равенстве средних

3.4. ПРОВЕРКА ГИПОТЕЗ О ВИДЕ РАСПРЕДЕЛЕНИЯ

Другой группой статистических гипотез являются гипотезы о проверке вида распределения: неизвестен вид распределения генеральной совокупности, и в частности, неизвестна функция распределения F(x).

Пусть – выборка наблюдений случайной величины X. Проверяется гипотеза Н₀ о том, что случайная величина X имеет функцию распределения F(x).

Разобьем область возможных значений X на r интервалов Δ₁, Δ₂, …, Δr. Пусть n_i – число элементов выборки, принадлежащих интервалу Δ_i (i = 1, …, r); при малых значениях n_i интервалы объединяют таким образом, чтобы в каждом из них было n_i 5.

Используя предполагаемый закон распределения – с функцией F(x), c учетом оценок параметров этого закона, найденных по выборке, находят вероятности того, что значения X принадлежат интервалу _Δi,то есть

Статистика

имеет распределение с числом степеней свободы (r – l – 1), где r – число интервалов, l – число неизвестных параметров распределения. Например, для нормального распределения l = 2 (неизвестные параметры m и σ).

Cчитается, что гипотеза Н₀ согласуется с опытом, если , где – выборочное значение статистики, – квантиль порядка (1 – α) распределения c числом степеней свободы (r – l – 1).

Рассмотренный метод проверки гипотезы вида распределения называется критерием хи-квадрат или критерием согласия Пирсона.

ЗАДАНИЕ

Дана выборка из 100 наблюдений; определить числовые характеристики, построить гистограмму частот, проверить нормальность распределения по критерию хи-квадрат.

Порядок проведения расчетов и оформление – в соответствии с рис. 3.7.

12,01	12,00	11,64	12,09	11,79
11,64	11,99	11,70	11,79	12,16
11,59	11,45	11,90	11,86	12,25
11,40	11,84	12,15	11,79	11,92
12,37	12,00	11,93	11,98	11,72
11,76	11,97	12,25	11,76	11,90
11,70	11,58	12,10	12,39	11,74
12,04	11,58	11,81	12,13	12,09
12,02	12,16	11,94	12,20	11,66
12,01	11,35	12,20	11,84	11,84
12,07	12,15	12,10	11,52	11,84
11,58	11,78	11,79	11,78	11,83
12,07	11,42	12,08	12,03	12,03
11,79	11,80	12,70	11,65	11,96
12,19	11,85	12,42	11,72	12,40
12,34	12,15	11,65	12,27	11,81
11,91	12,03	12,16	12,11	11,92
11,81	11,74	12,54	11,98	11,84
11,90	11,73	11,90	11,67	12,40
11,81	11,74	12,14	12,25	11,93

Рис. 3.7. Образец оформления рабочего листа при проверке гипотезы о нормальности распределения

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Оценки степени удовлетворенности 12 случайно отобранных клиентов фирмы (по 100-балльной системе) оказались такими: 89, 98, 96, 65, 99, 81, 76, 51, 82, 90, 96, 76. Существенно ли отличается среднее значение оценки от запланированных 80 баллов?

2. Телефонная компания обеспокоена нарушениями связи. Два подразделения компании занимаются устранением повреждений. Длительность ремонта в первом подразделении: 1,48; 1,75; 0,78; 2,85; 0,52; 1,60; 4,15; 3,97; 1,48; 3,10; 1,02; 0,53; 0,93; 1,60; 0,80; 1,05; 6,32; 3,93; 5,45; 0,97; во втором – 7,55; 3,75; 0,10; 1,10; 0,60; 0,52; 3,30; 2,10; 0,58; 4,02; 3,75; 4,23. 49

Можно ли утверждать, что оба ремонтных подразделения работают одинаково эффективно?

3. Директор центра обучения сотрудников крупной компании, занимающейся сборкой электронной аппаратуры, хочет сравнить эффективность двух методов подготовки работников конвейера. Группа 1 занимается по индивидуальным программам обучения, группа 2 – по коллективным. Эффективность обучения оценивалась по времени, затраченному на сборку изделия. Данные по группе 1: 22, 34, 52, 62, 30, 40, 64, 84, 56, 59; группе 2: 64, 45, 57, 64, 32, 88, 76.

ЛАБОРАТОРНАЯ РАБОТА №4. РЕГРЕССИОННЫЙ АНАЛИЗ

4.1. ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Пусть переменная Х принимает некоторые фиксированные значения х₁, х₂, …, х_n. Соответствующие значения зависимой переменной Y имеют разброс вследствие погрешности измерений и различных неучтенных факторов и оказались равными y₁, y₂, …, y_n.

Если предположить, что связь между переменными линейна, то соответствующая регрессионная модель имеет вид

где и – параметры линейной регрессии, – случайная ошибка наблюдения; предполагается, что математическое ожидание М() = 0, а дисперсия D() = постоянна.

Задача регрессионного анализа сводится к оценке параметров регрессии и , проверке гипотезы о значимости модели и оценке её адекватности – достаточно ли хорошо согласуется модель с результатами наблюдений?

Для оценки параметров регрессии используется метод наименьших квадратов: в качестве оценок принимаются такие значения и , которые минимизируют сумму квадратов отклонений наблюдаемых значений от расчетных точек . Для парной линейной модели эти оценки определяются по формулам:

где

Расчетное значение (прогноз) . Разности между наблюдаемыми и расчетными значениями , называются остатками, а соответствующая сумма квадратов – остаточной суммой квадратов:

Сумма квадратов, обусловленная регрессией

Линейная регрессионная модель называется незначимой, если параметр . Для проверки соответствующей нулевой гипотезы используется статистика Фишера

которая при заданном уровне значимости сравнивается с квантилью с числом степеней свободы 1 и (n – 2); если оказывается 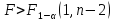, то нулевая гипотеза отклоняется и говорят, что регрессионная модель статистически значима.

Для характеристики качества той или иной модели может быть использован коэффициент детерминации – квадрат коэффициента корреляции между опытными и прогнозируемыми значениями:

Чем ближе коэффициент детерминации к единице, тем более качественной считается модель.

Для проведения регрессионного анализа в Excel могут быть использованы как статистические функции, так и функции массива. Среди статистических четыре функции предназначены для расчета парной линейной регрессии – вычисления коэффициентов (ОТРЕЗОК) и (НАКЛОН), расчета прогнозируемых значений (ПРЕДСКАЗ) и определения коэффициента детерминации (КВПИРСОН).

Функция ОТРЕЗОК (рис. 4.1) вычисляет точку пересечения линии с осью y, используя значения аргументов «известные_значения_x» и «известные_значения_y». Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные значениями в аргументах «известные_значения_x» и «известные_значения_y». Функция ОТРЕЗОК используется, когда нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.

Синтаксис

ОТРЕЗОК(известные_значения_x;известные_значения_y)

здесь Известные_значения_y   — зависимое множество наблюдений или данных.

Известные_значения_x   — независимое множество наблюдений или данных.

Рис. 4.1. Встроенная статистическая функция ОТРЕЗОК

Замечания:

Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

Если значения аргументов «известные_значения_y» и «известные_значения_x» содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.

Уравнение для точки пересечения линии линейной регрессии a имеет следующий вид:

где наклон b вычисляется следующим образом:

где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Алгоритм, положенный в основу работы функций ОТРЕЗОК и НАКЛОН отличается от алгоритма, на котором построена функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать, в случае недоопределенных и коллинеарных данных. Например, если точками данных аргумента «известные_значения_y» являются нули, а аргумента «известные_значения_x» — единицы, то:

Функции ОТРЕЗОК и НАКЛОН возвратят ошибку #ДЕЛ/0!. Алгоритм, используемый в функциях ОТРЕЗОК и НАКЛОН, предназначен для поиска единственного решения, а в этом случае решений может быть несколько.

Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.

Пример 4.1

1 2 3 4 5 6

A B Известные значения y Известные значения x 2 6 3 5 9 11 1 7 8 5 Формула Описание (результат) =ОТРЕЗОК(A2:A6; B2:B6) Указывает на точку пересечения линии с осью y, используя приведенные выше известные_значения_x и известные_значения_y (0,0483871)

Функция НАКЛОН возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой; иными словами, наклон — это скорость изменения значений вдоль прямой.

Синтаксис

НАКЛОН(известные_значения_y;известные_значения_x)

здесь Известные_значения_y  — массив или интервал ячеек, содержащих числовые зависимые точки данных.

Известные_значения_x  — множество независимых точек данных

Рис. 4.2. Встроенная статистическая функция НАКЛОН

Замечания аналогичны замечаниям функции ОТРЕЗОК.

Пример 4.2

1 2 3 4 5 6 7 8

A B Известные значения y Известные значения x 2 6 3 5 9 11 1 7 8 5 7 4 5 4 Формула Описание (результат) =НАКЛОН(A2:A8;B2:B8) Наклон линии линейной регрессии для указанных выше точек данных (0,305556)

Функция ПРЕДСКАЗ вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это y-значение, соответствующее заданному x-значению. x- и y-значения — известны; новое значение предсказывается с использованием линейной регрессии. Этой функцией можно воспользоваться для прогнозирования будущих продаж, потребностей в оборудовании или тенденций потребления.

Синтаксис:

ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x)

здесь x  — точка данных, для которой предсказывается значение.

Известные_значения_y  — зависимый массив или интервал данных.

Известные_значения_x  — независимый массив или интервал данных.

Замечания:

Если «x» не является числом, функция ПРЕДСКАЗ возвращает значение ошибки #ЗНАЧ!.

Если аргументы «известные_значения_y» и «известные_значения_x» пусты или количество точек данных в этих аргументах не совпадает, функция ПРЕДСКАЗ возвращает значение ошибки #Н/Д.

Рис. 4.3. Встроенная статистическая функция ПРЕДСКАЗ

Если дисперсия аргумента «известные_значения_x» равна 0, функция ПРЕДСКАЗ возвращает значение ошибки #ДЕЛ/0!.

Уравнение для ПРЕДСКАЗ имеет вид a + bx, где:

и

где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Пример 4.3

1 2 3 4 5 6

A B Известные значения y Известные значения x 6 20 7 28 9 31 15 38 21 40 Формула Описание (результат) =ПРЕДСКАЗ(30;A2:A6;B2:B6) Предсказывает y-значение, соответствующее заданному x-значению 30 (10,60725)

Функция КВПИРСОН возвращает квадрат коэффициента корреляции Пирсона для точек данных в аргументах известные_значения_y и известные_значения_x. Значение r-квадрат можно интерпретировать как отношение дисперсии для y к дисперсии для x.

Синтаксис:

КВПИРСОН(известные_значения_y;известные_значения_x)

здесь Известные_значения_y  — массив или интервал точек данных.

Известные_значения_x  — массив или интервал точек данных.

Замечания:

Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.

Учитываются логические значения и текстовые представления чисел, которые введены непосредственно в список аргументов.

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, приводят к возникновению ошибки.

Если аргументы известные_значения_y и известные_значения_x пусты или указанное в них количество число точек данных не совпадает, функция КВПИРСОН возвращает значение ошибки #Н/Д.

Если аргументы известные_значения_y и известные_значения_x содержат только одну точку данных, функция КВПИРСОН возвращает значение ошибки #ДЕЛ/0!.

Коэффициент корреляции Пирсона (r) вычисляется с помощью следующего уравнения:

где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Функция КВПИРСОН возвращает значение r², являющееся квадратом коэффициента корреляции.

Пример 4.4

1 2 3 4 5 6 7 8

A B Известные значения y Известные значения x 2 6 3 5 9 11 1 7 8 5 7 4 5 4 Формула Описание (результат) =КВПИРСОН(A2:A8;B2:B8) Квадрат коэффициента корреляции Пирсона для указанных точек данных (0,05795)

Вторая группа функций, предназначенных для проведения регрессионного анализа, - это функции массива: эти функции могут быть использованы как для проведения парной линейной регрессии, так и для нелинейной и множественной регрессии: ЛИНЕЙН – линейная регрессия, ТЕНДЕНЦИЯ – прогноз по линейной регрессии, ЛГРФПРИБЛ – экспоненциальная регрессия, РОСТ – прогноз по экспоненциальной регрессии.

Функция ЛИНЕЙН возвращает параметры линейного тренда, рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Можно также объединять функцию ЛИНЕЙН с другими функциями для вычисления других видов моделей, являющихся линейными в неизвестных параметрах (неизвестные параметры которых являются линейными), включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.

Уравнение для прямой линии имеет следующий вид:

y = mx + b или

y = m1x1 + m2x2 + ... + b (в случае нескольких диапазонов значений x),

где зависимое значение y — функция независимого значения x, значения m — коэффициенты, соответствующие каждой независимой переменной x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {mn;mn-1;...;m1;b}. ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.

Синтаксис:

ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)

где Известные_значения_y  - множество значений y, которые уже известны для соотношения y = mx + b.

Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.

Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x  — необязательное множество значений x, которые уже известны для соотношения y = mx + b.

Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).

Если массив_известные_значения_x опущен, то предполагается, что этот массив {1;2;3;...} имеет такой же размер, как и массив_известные_значения_y.

Конст  — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

Если аргумент «конст» имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.

Если аргумент «конст» имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

Статистика  — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

Если аргумент «статистика» имеет значение ИСТИНА, функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Возвращаемый массив будет иметь следующий вид: {mn;mn-1;...;m1;b:sen;sen-1;...;se1;seb:r2;sey:F;df:ssreg;ssresid}.

Если аргумент «статистика» имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

Дополнительная регрессионная статистика.

Величина	Описание
se1,se2,...,sen	Стандартные значения ошибок для коэффициентов m1,m2,...,mn.
seb	Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент «конст» имеет значение ЛОЖЬ).
r2	Коэффициент детерминированности. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т. е. различия между фактическим и оценочным значениями y не существует. В противоположном случае, если коэффициент детерминированности равен 0, использовать уравнение регрессии для предсказания значений y не имеет смысла. Для получения дополнительных сведений о способах вычисления r2, см. «Замечания» в конце данного раздела.
sey	Стандартная ошибка для оценки y.
F	F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
df	Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Для получения дополнительных сведений о вычислении величины df см. «Замечания» в конце данного раздела. Далее в примере 4 показано использование величин F и df.
ssreg	Регрессионная сумма квадратов.
ssresid	Остаточная сумма квадратов. Для получения дополнительных сведений о расчете величин ssreg и ssresid см. «Замечания» в конце данного раздела.

На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.

Замечания:

Любую прямую можно описать ее наклоном и пересечением с осью y:

Наклон - (m): чтобы определить наклон прямой, обычно обозначаемый через m, нужно взять две точки прямой (x1,y1) и (x2,y2); наклон будет равен (y2 - y1)/(x2 - x1).

Y-пересечение (b): Y-пересечением прямой, обычно обозначаемым через b, является значение y для точки, в которой прямая пересекает ось y.

Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.

Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:

Наклон: ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);1)

Y-пересечение: ИНДЕКС(ЛИНЕЙН(известные_значения_y;известные_значения_x);2)

Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. Когда имеется только одна независимая переменная x,

Рис. 4.4. Встроенная функция массива ЛИНЕЙН m и b вычисляются по следующим

формулам:

где x и y – выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ(известные_значения_y).

Функции аппроксимации ЛИНЕЙН и ЛГРФПРИБЛ могут вычислить прямую или экспоненциальную кривую, наилучшим образом описывающую данные. Однако они не дают ответа на вопрос, какой из двух результатов больше подходит для решения поставленной задачи. Можно также вычислить функцию ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x) для прямой или функцию РОСТ(известные_значения_y; известные_значения_x) для экспоненциальной кривой. Эти функции, если не задавать аргумент новые_значения_x, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. После этого можно сравнить вычисленные значения с фактическими значениями. Можно также построить диаграммы для визуального сравнения.

Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal - ssresid. Чем меньше остаточная сумма квадратов, тем больше значение коэффициента детерминированности r², который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Коэффициент r² равен ssreg/sstotal.

В некоторых случаях один или более столбцов X (пусть значения Y и X находятся в столбцах) не имеет дополнительного предикативного значения в других столбцах X. Другими словами, удаление одного или более столбцов X может привести к значениям Y, вычисленным с одинаковой точностью. В этом случае избыточные столбцы X будут исключены из модели регрессии. Этот феномен называется «коллинеарностью», поскольку избыточные столбцы X могут быть представлены в виде суммы нескольких неизбыточных столбцов. Функция ЛИНЕЙН проверяет на коллинеарность и удаляет из модели регрессии все избыточные столбцы X, если обнаруживает их. Удаленные столбцы X можно определить в выходных данных ЛИНЕЙН по коэффициенту, равному 0, и по значению se, равному 0. Удаление одного или более столбцов как избыточных изменяет величину df, поскольку она зависит от количества столбцов X, в действительности используемых для предикативных целей. При изменении df вследствие удаления избыточных столбцов значения sey и F также изменяются. Часто использовать коллинеарность не рекомендуется. Однако ее следует применять, если некоторые столбцы X содержат 0 или 1 в качестве индикатора указывающего, входит ли предмет эксперимента в отдельную группу. Если конст = ИСТИНА или значение этого аргумента не указано, функция ЛИНЕЙН вставляет дополнительный столбец X для моделирования точки пересечения. Если имеется столбец со значениями 1 для указания мужчин и 0 — для женщин, а также имеется столбец со значениями 1 для указания женщин и 0 — для мужчин, то последний столбец удаляется, поскольку его значения можно получить из столбца с «индикатором мужского пола».

Вычисление df для случаев, когда столбцы X не удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n - k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.

Формулы, которые возвращают массивы, должны быть введены как формулы массива.

При вводе массива констант в качестве, например, аргумента известные_значения_x следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть различными в зависимости от параметров, заданных в окне Язык и стандарты на панели управления.

Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.

Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:

Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.

Функции НАКЛОН и ОТРЕЗОК возвращают ошибку #ДЕЛ/0!. Алгоритм функций НАКЛОН и ОТРЕЗОК используется для поиска только одного ответа, а в данном случае их может быть несколько.

Помимо вычисления статистики для других типов регрессии функцию ЛИНЕЙН можно использовать при вычислении диапазонов для других типов регрессии, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:

=ЛИНЕЙН(значения_y, значения_x^СТОЛБЕЦ($A:$C))

работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:

y = m1*x + m2*x^2 + m3*x^3 + b

Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.

Пример 4.5. Наклон и Y-пересечение

1 2 3 4 5

A B Известные значения y Известные значения x 1 0 9 4 5 2 7 3 Формула Формула =ЛИНЕЙН(A2:A5;B2:B5;;ЛОЖЬ)

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон A7:B7, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственное значение будет равно 2.

Если формула вводится как формула массива, возвращается наклон (2) и y-пересечение (1).

Пример 4.6. Простая линейная регрессия

1 2 3 4 5 6 7

A B Месяц Продажи 1 3100 2 4500 3 4400 4 5400 5 7500 6 8100 Формула Описание (результат) =СУММ(ЛИНЕЙН(B2:B7; A2:A7)*{9;1}) Оценивает количество продаж за девятый месяц (11000)

В общем случае СУММ({m;b}*{x;1}) равняется mx + b, то есть значению y для данного значения x. Для этих же целей можно воспользоваться функцией ТЕНДЕНЦИЯ.

Функция ТЕНДЕНЦИЯ возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов) массивы «известные_значения_y» и «известные_значения_x». Возвращает значения y, соответствующие этой прямой для заданного массива «новые_значения_x».

Синтаксис:

ТЕНДЕНЦИЯ(известные_значения_y;известные_значения_x;новые_значения_x;конст)

здесь Известные_значения_y  - множество значений y, которые уже известны для соотношения y = mx + b.

Если массив «известные_значения_y» имеет один столбец, то каждый столбец массива «известные_значения_x» интерпретируется как отдельная переменная.

Если массив «известные_значения_y» имеет одну строку, то каждая строка массива «известные_значения_x» интерпретируется как отдельная переменная.

Известные_значения_x  — необязательное множество значений x, которые уже известны для соотношения y = mx + b.

Массив «известные_значения_x» может содержать одно или несколько множеств переменных. Если используется только одна переменная, то аргументы «известные_значения_y» и «известные_значения_x» могут быть диапазонами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то аргумент «известные_значения_y» должен быть вектором (то есть диапазоном высотой в одну строку или шириной в один столбец).

Если аргумент «известные_значения_x» опущен, то предполагается, что это массив {1;2;3;...} того же размера, что и массив «известные_значения_y».

Новые_значения_x  — новые значения x, для которых функция ТЕНДЕНЦИЯ возвращает соответствующие значения y.

Аргумент «новые_значения_x», так же как и аргумент «известные_значения_x», должен содержать по одному столбцу (или строке) для каждой независимой переменной. Таким образом, если «известные_значения_y» — это один столбец, то «известные_значения_x» и «новые_значения_x» должны иметь одинаковое количество столбцов. Если «известные_значения_y» — это одна строка, то аргументы «известные_значения_x» и «новые_значения_x» должны иметь одинаковое количество строк.

Если аргумент «новые_значения_x» опущен, то предполагается, что он совпадает с аргументом «известные_значения_x».

Если опущены оба аргумента — «известные_значения_x» и «новые_значения_x», — то предполагается, что это массивы {1;2;3;...} того же размера, что и «известные_значения_y».

Конст  - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.

Если аргумент «конст» имеет значение ИСТИНА или опущен, то b вычисляется обычным образом.

Если аргумент «конст» имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось условие y = mx.

Замечания:

Функцию ТЕНДЕНЦИЯ можно использовать для аппроксимации полиномиальной кривой, проводя регрессионный анализ для той же переменной, возведенной в различные степени. Например, пусть столбец A содержит значения y, а столбец B содержит значения x. Можно ввести значение x^2 в столбец C, x^3 в столбец D и т. д., а затем провести регрессионный анализ столбцов от B до

Рис. 4.5. Встроенная функция массива ТЕНДЕНЦИЯ D со столбцом A.

Формулы, которые возвращают массивы, должны быть введены как формулы массива.

При вводе константы массива для таких аргументов, как «известные_значения_x», следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.

Пример 4.7

Первая формула показывает значения, соответствующие известным значениям. Вторая формула предсказывает значения для следующих месяцев, если линейный тренд сохраняется.

1 2 3 4 5 6 7 8 9 10 11 12 13

А B C Месяц Цена Формула (соответствующая цена) 1 133 890р. =ТЕНДЕНЦИЯ(B2:B13;A2:A13) 2 135 000р. 3 135 790р. 4 137 300р. 5 138 130р. 6 139 100р. 7 139 900р. 8 141 120р. 9 141 890р. 10 143 230р. 11 144 000р. 12 145 290р. Месяц Формула (предполагаемая цена) 13 =ТЕНДЕНЦИЯ(B2:B13;A2:A13;A15:A19) 14 15 16 17

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон C2:C13 или B15:B19, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственные значения будут равны 133953,3333 и 146171,5152.

Функция ЛГРФПРИБЛ служит для расчета корректировки для введенных данных в виде кривой экспоненциальной регрессии. В регрессионном анализе вычисляется экспоненциальная кривая, аппроксимирующая данные, и возвращается массив значений, описывающий эту кривую. Поскольку данная функция возвращает массив значений, она должна вводиться как формула массива.

Уравнение кривой имеет следующий вид:

y = b*m^x или

y = (b*(m1^x1)*(m2^x2)*_) (в случае нескольких значений x),

где зависимые значения y являются функцией независимых значений x. Значения m являются основанием, возводимым в степень x, а значения b постоянны. Заметим, что y, x и m могут быть векторами. Функция ЛГРФПРИБЛ возвращает массив {mn;mn-1;...;m1;b}.

Синтаксис:

ЛГРФПРИБЛ(известные_значения_y;известные_значения_x;конст;статистика)

здесь Известные_значения_y  — множество значений y, которые уже известны в соотношении y = b*m^x.

Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.

Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x  — необязательное множество значений x, которые уже известны для соотношения y = b*m^x.

Массив известные_значения_x может включать одно или более множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут быть диапазонами любой формы, если только они имеют одинаковые размерности. Если используется более одной переменной, то аргумент известные_значения_y должен быть диапазоном ячеек высотой в одну строку или шириной в один столбец (так называемым вектором).

Если аргумент известные_значения_x опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как и известные_значения_y.

Конст  — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1.

Если аргумент «конст» имеет значение ИСТИНА или опущен, то b вычисляется обычным образом.

Если аргумент «конст» имеет значение ЛОЖЬ, то b полагается равным 1 и значения m подбираются так, чтобы удовлетворить соотношению y = m^x.

Статистика  — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

Если аргумент «статистика» имеет значение ИСТИНА, функция ЛГРФПРИБЛ возвращает дополнительную статистику по регрессии, т. е. возвращает массив {mn;mn-1;...;m1;b:sen;sen-1;...;se1;seb:r 2;sey;F;df:ssreg;ssresid}.

Если аргумент «статистика» имеет значение ЛОЖЬ или опущен, функция ЛГРФПРИБЛ возвращает только коэффициенты m и константу b.

Замечания:

Чем больше график ваших данных напоминает экспоненциальную кривую, тем лучше вычисленная кривая будет аппроксимировать данные. Подобно функции ЛИНЕЙН, функция ЛГРФПРИБЛ возвращает массив, который описывает зависимость между значениями, но ЛИНЕЙН подгоняет прямую линию к имеющимся данным, а ЛГРФПРИБЛ подгоняет

Рис. 4.6. Встроенная функция массива ЛГРФПРИБЛ экспоненциальную кривую.

Если имеется только одна независимая переменная x, то значения пересечения с осью y (b) можно получить непосредственно, используя следующую формулу:

Пересечение с осью y (b):

ИНДЕКС(ЛГРФПРИБЛ(известные_значения_y;известные_значения_x);2)

Можно использовать уравнение y = b*m^x для предсказания будущих значений y, но в Microsoft Excel предусмотрена функция РОСТ для этой цели.

Формулы, которые возвращают массивы, должны быть введены как формулы массива.

При вводе массива констант в качестве, например, аргумента известные_значения_x, следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть различными в зависимости от параметров, заданных в окне Язык и стандарты на панели управления.

Следует помнить, что значения y, предсказанные с помощью уравнения регрессии, могут быть недостоверными, если они находятся вне диапазона значений y, которые использовались для определения коэффициентов уравнения.

Пример 4.8. Коэффициенты m и константа b

1 2 3 4 5 6 7

A B Месяц Единицы 11 33 100 12 47 300 13 69 000 14 102 000 15 150 000 16 220 000 Формула Формула =ЛГРФПРИБЛ(B2:B7;A2:A7; ИСТИНА; ЛОЖЬ)

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон A9:B9, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственное значение будет равно 1,463275628.

Если формула вводится как формула массива, возвращаются коэффициенты m и константа b.

y = b*m1^x1 или, используя значения из массива:

y = 495,3 * 1,4633x

Можно оценить количество продаж в последующие месяцы либо подставив номер месяца в качестве x в это уравнение, либо воспользовавшись функцией РОСТ.

Пример 4.9. Полная статистика

1 2 3 4 5 6 7

A B Месяц Единицы 11 33 100 12 47 300 13 69 000 14 102 000 15 150 000 16 150 000 Формула =ЛГРФПРИБЛ(B2:B7;A2:A7; ИСТИНА; ИСТИНА)

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон A9:B13, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем — клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственное значение будет равно 1,463275628.

Если формула вводится как формула массива, возвращается следующая статистика по регрессии. Используйте эту клавишу для определения нужной статистики.

Можно использовать дополнительную статистику по регрессии (в приведенном выше примере — ячейки A10:B13), чтобы оценить, насколько полезно полученное уравнение для предсказания будущих значений.

Важно.  Методы, которые используются для проверки уравнений, полученных с помощью функции ЛГРФПРИБЛ, такие же, как и для функции ЛИНЕЙН. Однако дополнительная статистика, которую возвращает функция ЛГРФПРИБЛ, основана на следующей линейной модели:

ln y = x1 ln m1 + ... + xn ln mn + ln b

Это следует помнить при оценке дополнительной статистики, особенно значений sei и seb, которые следует сравнивать с ln mi и ln b, а не с mi и b. Дополнительные сведения имеются в любом справочнике по математической статистике.

Функция РОСТ служит для расчета точек экспоненциального тренда в массиве. Рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений. Функция рабочего листа РОСТ может применяться также для для аппроксимации существующих x- и y-значений экспоненциальной кривой.

Синтаксис:

РОСТ(известные_значения_y;известные_значения_x;новые_значения_x;конст)

здесь Известные_значения_y   — множество значений y, которые уже известны в уравнении y = b*m^x.

Если массив «известные_значения_y» содержит один столбец, каждый столбец массива «известные_значения_x» интерпретируется как отдельная переменная.

Если массив «известные_значения_y» содержит одну строку, каждая строка массива «известные_значения_x» интерпретируется как отдельная переменная.

Если какие-либо числа в массиве «известные_значения_y» равны 0 или имеют отрицательное значение, функция РОСТ возвращает значение ошибки #ЧИСЛО!.

Известные_значения_x   — необязательное множество значений x, которые уже известны в уравнении y = b*m^x.

Массив «известные_значения_x» может содержать одно или несколько множеств переменных. Если используется только одна переменная, множества «известные_значения_y» и «известные_значения_x» могут иметь любую длину, но их размерности должны совпадать. Если используется более одной переменной, аргумент «известные_значения_y» должен быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).

Если аргумент «известные_значения_x» опущен, то предполагается, что это массив {1;2;3;...} того же размера, что и «известные_значения_y».

Новые_значения_x   — новые значения x, для которых РОСТ возвращает соответствующие значения y.

Аргумент «новые_значения_x» должен содержать столбец (или строку) для каждой независимой переменной, так же как и «известные_значения_x». Таким образом, если массив «известные_значения_y» состоит из одного столбца, то столько же столбцов должны иметь массивы «известные_значения_x» и «новые_значения_x». Если массив «известные_значения_y» состоит из одной строки, столько же строк должно содержаться в массивах «известные_значения_x» и «новые_значения_x».

Если аргумент «новые_значения_x» опущен, предполагается, что он совпадает с аргументом «известные_значения_x».

Если опущены оба аргумента «известные_значения_x» и «новые_значения_x», то предполагается, что каждый из них представляет собой массив {1;2;3;...} того же размера, что и «известные_значения_y».

Конст   — логическое значение, которое указывает, должна ли константа b равняться 1.

Если аргумент «конст» имеет значение ИСТИНА или опущен, b вычисляется обычным образом.

Если аргумент «конст» имеет значение ЛОЖЬ, то предполагается, что b = 1, а значения m подбираются таким образом, чтобы выполнялось равенство y = m^x.

Замечания:

Формулы, возвращающие массивы, должны быть введены как формулы массивов после того, как будет выделено соответствующее количество ячеек.

При вводе константы массива для аргумента (например, «известные_значения_x») следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.

Пример 4.10

1 2 3 4 5 6 7

A B C Месяц Единицы Формула (Соответственные единицы) 11 33 100 =РОСТ(B2:B7;A2:A7) 12 47 300 13 69 000 14 102 000 15 150 000 16 220 000 Месяц Формула (Предполагаемые единицы) 17 =РОСТ(B2:B7;A2:A7; A9:A10) 18

 Примечание.    Формулу в этом примере необходимо ввести как формулу массива. После копирования примера на пустой лист выделите диапазон C2:C7 или B9:B10, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем клавиши CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, единственные значения будут равны 32 618,20377 и 320 196,7184.

ЗАДАНИЕ

Связь между пределом прочности прессованной детали у и температурой при прессовании x предполагается линейной. По полученным опытным данным построить парную линейную регрессионную модель.

x	120	125	130	135	140	145	150	155	160	165
y	110	107	105	98	100	95	95	92	86	83

Провести расчет двумя способами: с использованием встроенных статистических функций и функций массива. Результаты расчета оформить в соответствии с образцом по рис. 4.3.

4.2. ПАРНАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ

В общем случае, когда линейная регрессионная модель оказывается неадекватной опытным данным, рассматривают нелинейные модели (в частности, нелинейные по фактору х, но линейные по параметрам ):

где – неизвестные параметры, а (x) – известные базисные функции.

Рис. 4.3. Образец оформления рабочего листа при проведении парного линейного регрессионного анализа

Они могут быть степенными , тригонометрическими и т.д. Параметры , как и ранее, оцениваются методом наименьших квадратов.

В частности, если рассматривается гиперболическая модель вида

(при этом в уравнении (4.9) k = 2, (x) = 1 / x, при j > 1 (x) = 0), получим систему вида

Для параболической модели

(k = 3, (x) = x, (x) = при j > 2 (x) = 0), получим систему вида

Мы рассмотрели регрессионные модели, нелинейные по фактору х, но линейные по параметрам . Во многих практических задачах зависимость между x и Y нелинейна и по параметрам. В этом случае по возможности пытаются свести нелинейную по параметрам модель к модели вида (4.9).

Пусть, например, зависимость между переменными z и х имеет вид

Введя новую переменную y = 1 / z, получим линейную модель.

Если, например,

то, логарифмируя и вводя переменную y = lnx, также приходим к линейной модели.

По аналогии с линейной регрессией может быть проведена проверка значимости модели.

Очевидно, что для описания одного набора опытных данных можно использовать различные модели вида (4.9), которые окажутся и значимыми, и адекватными. Для характеристики качества той или иной модели может быть использован коэффициент детерминации: чем ближе коэффициент детерминации к единице, тем более качественной считается модель.

Часто для качественного анализа опытного набора точек полезно использовать графические средства Excel. Построив диаграмму рассеяния, с помощью контекстного меню Свойства объекта / Статистика можно построить некоторые линии регрессии (рис. 4.4).

Рис. 4.4. Построение кривых регрессии

ЗАДАНИЕ

Проанализировать зависимость урожайности у от количества осадков х:

х	24	26	29	34	35	37	39	40	41	44	47	48	50	52	55
у	22	23	25	27	31	30	31	32	32	31	30	29	26	22	24

1. Построить диаграмму рассеяния с кривыми линейной, логарифмической и экспоненциальной регрессии.

2. Используя встроенные статистические функции, найти параметры парной линейной регрессии и коэффициент детерминации.

3. Используя встроенные статистические функции, найти параметры парной гиперболической регрессии и коэффициент детерминации (предварительно необходимо подготовить столбец преобразованных данных: в качестве аргумента Данные_Х ввести значения 1/х).

4. Используя функцию массива ЛГРФПРИБЛ, найти параметры парной экспоненциальной регрессии и коэффициент детерминации.

5. Используя функцию массива ЛИНЕЙН, найти параметры парной параболической регрессии и коэффициент детерминации (предварительно необходимо подготовить столбец со значениями x²).

6. Определить, используя коэффициент детерминации, какая из моделей лучше соответствует опытным данным; для этой модели вычислить прогнозируемые значения отклика (используя встроенные функции или непосредственно по найденному уравнению регрессии) и построить диаграмму рассеяния с наложенной линией регрессии (оформить расчеты в соответствии с рис. 4.5).

Рис. 4.5. Образец оформления рабочего листа при проведении парного нелинейного регрессионного анализа

4.3. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ

В множественном регрессионном анализе исследуется зависимость случайной величины Y от нескольких независимых переменных x1, x2, …, xk -1. Линейная регрессионная модель имеет вид

или в матричной форме

Y = Х + , (4.15)

где – вектор наблюдений, содержащий n значений откликов,

– вектор неизвестных параметров регрессии, подлежащих оцениванию,

– вектор ошибок (предполагается, что ошибки распределены по нормальному закону с нулевым математическим ожиданием и постоянной дисперсией, некоррелированы и независимы),

– регрессионная матрица, содержащая элементы x_ij (регрессоры) – результаты i-го наблюдения за j-й переменной.

Оценки параметров модели (4.15) по методу наименьших квадратов определяются по формуле

, (4.16)

Для проверки значимости модели в качестве нулевой рассматривается гипотеза

о том, что все регрессоры x_j не оказывают существенного влияния на отклик.

Соответствующая статистика

сравнивается с квантилью распределения Фишера .

В формуле (4.17)

Если нулевая гипотеза отклоняется, регрессионная модель статистически значима. При незначимости линейной модели рассматриваются более сложные модели.

Если же модель оказалась значимой, далее проверяется значимость каждого регрессора: выдвигается предположение о том, что регрессор x_j незначим. Соответствующая нулевая гипотеза . Для ее проверки используется статистика

где s_j – среднеквадратичное отклонение (стандартная ошибка) параметра , определяемое по формуле

где c_jj – диагональные элементы матрицы . Найденное по формуле (4.18) значение сравнивается с квантилью распределения Стьюдента . При незначимости соответствующий регрессор удаляется из модели, и расчет проводится заново.

ЗАДАНИЕ

Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе.

Застройщик может воспользоваться множественным регрессионным анализом для оценки цены офисного здания в заданном районе на основе следующих переменных.

Переменная	Смысл переменной
y	Оценочная цена здания под офис
x1	Общая площадь в квадратных метрах
x2	Количество офисов
x3	Количество входов
x4	Время эксплуатации здания в годах

В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (x1, x2, x3 и x4) и зависимой переменной (y), т. е. ценой здания под офис в данном районе.

Застройщик наугад выбирает 11 зданий из имеющихся 1500 и получает данные, которые приведены ниже. «0,5» входа означает вход только для доставки корреспонденции.

1. Найти оценки параметров модели и коэффициент детерминации.

2. Проверить значимость модели.

3. Проверить значимость каждого фактора.

4. Расчет оформить в соответствии с образцом по рис. 4.6.

№ п/п 1 2 3 4 5 6 7 8 9 10 11 12

A B C D E Общая площадь (x1) Количество офисов (x2) Количество входов (x3) Время эксплуатации (x4) Оценочная цена (y) т.р. 2310 2 2 20 142 000 2333 2 2 12 144 000 2356 3 1,5 33 151 000 2379 3 2 43 150 000 2402 2 3 53 139 000 2425 4 2 23 169 000 2448 2 1,5 99 126 000 2471 2 2 34 142 900 2494 3 3 23 163 000 2517 4 4 55 169 000 2540 2 3 22 149 000

Рис. 4.6. Образец оформления рабочего листа при проведении множественного регрессионного анализа

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. За каждым из 9 менеджеров по сбыту закреплена определенная территория. В таблице приведены численность населения на этой территории Х в млн чел. и объемы продаж, обеспеченные соответствующим менеджером, У в млн у. е. Построить парную линейную регрессию, проанализировать качество работы менеджеров.

№	1	2	3	4	5	6	7	8	9
x	4,96	8,26	9,09	12,25	4,73	13,68	3,58	2,77	4,64
y	2,69	3,54	3,32	3,54	2,25	5,15	2,02	1,71	3,26

2. Давление в системе y в МПа в зависимости от времени выдержки х в мин может быть аппроксимировано линейной или параболической зависимостями. Оценить параметры этих зависимостей и выяснить, какая из них лучше отображает результаты наблюдений, если получены следующие опытные данные:

x	0	1	2	3	4	5	6
y	0,40	0,20	0,10	0,06	0,04	0,03	0,02

3. Изучалось влияние на влажность вафельного листа у времени выдержки листа в печи х1, температуры печи х2 и влажности теста х3. Проведено 20 наблюдений:

№	у	х1	х2	х3	№	у	х1	х2	х3
1	3,1	2,5	180	63	11	2,9	3	180	63
2	3,4	2,5	180	64	12	3,0	3	180	64
3	3,5	2,5	180	65	13	3,1	3	180	65
4	3,2	2,5	180	63	14	2,8	3	180	63
5	3,3	2,5	180	64	15	2,9	3	180	64
6	3,4	2,5	200	65	16	2,9	3	200	65
7	3,2	2,5	200	63	17	2,7	3	200	63
8	3,3	2,5	200	64	18	2,8	3	200	64
9	3,4	2,5	200	65	19	2,9	3	200	65
10	3,2	2,5	200	63	20	2,8	3	200	63

Требуется построить модель множественной регрессии, предполагая наличие линейной связи между влажностью вафельного листа и тремя указанными факторами.

ЛАБОРАТОРНАЯ РАБОТА №5. КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА

5.1. КАРТЫ СРЕДНИХ И РАЗМАХОВ

Статистическое управление процессами состоит в выявлении неслучайных нарушений процесса; при этом управляющее воздействие (регулирование) применяется тогда, когда выпускаемая продукция или услуга еще удовлетворяет заданным требованиям, но некоторые статистические показатели дают основание предполагать наличие неслучайной причины, которая приведет к нарушению процесса.

Изменение характеристик качества изделия в процессе изготовления обусловлено причинами двух типов. Одна группа причин связана с особенностями данного процесса – износом инструмента, ослаблением креплений, изменением температуры охлаждающей жидкости. Это неслучайные причины вариаций, которые могут быть устранены при настройке процесса. Другая группа причин – неустранимые, случайные причины изменчивости (колебания температуры окружающей среды, вариации характеристик материала и т. п.).

Технологический процесс желательно проводить так, чтобы изменчивость характеристик качества была обусловлена только случайными причинами. Неслучайные причины изменчивости процесса могут быть выявлены с помощью статистических методов. Управление технологическим процессом состоит в выявлении и устранении этих причин. Изменчивость за счет случайных причин может быть снижена только путем усовершенствования самого процесса.

Процесс считается статистически управляемым, если обеспечена его стабильность, то есть повторяемость контролируемых параметров. Статистическая управляемость еще не означает, что процесс удовлетворяет требованиям потребителя: стабильный процесс может не обеспечивать выполнение требуемых технических условий. В связи с этим, кроме оценки стабильности процесса, проверяется и его возможности: как соотносятся характеристики процесса с техническими условиями.

Контрольная карта Шухарта – графическое изображение мониторинга процесса. По горизонтальной оси откладываются моменты времени или номер измерения, по вертикальной – значения показателя качества. Проводятся также нижняя и верхняя контрольная границы (границы регулирования) и средняя линия. Если значение показателя оказалось на одной из контрольных границ или за ее пределами, то нулевая гипотеза о статистической управляемости процесса отклоняется, и процесс требует вмешательства (регулирования).

Карты по количественному признаку применяются тогда, когда контролируемый показатель можно измерить. Это может быть, например, диаметр вала, шероховатость поверхности, крутящий момент, прочность изделия, температура нагрева, электрическое сопротивление, вес изделия, влажность, содержание некоторого вещества в растворе, и т. п.

Обычно контролируется изменение как среднего значения показателя качества, характеризующего уровень настройки процесса, так и технологического рассеяния: строятся двойные карты Шухарта. При этом уровень настройки процесса может оцениваться по средним значениям или медианам, а рассеяние – по стандартным отклонениям или размахам.

В соответствии с этим чаще всего используются двойные карты следующих типов:

- карты средних значений и размахов ( - R - карты);

- карты средних значений и стандартных отклонений ( - s - карты);

- карты медиан и размахов (Ме - R - карты).

Процесс считается стабильным, или статистически управляемым, если об этом свидетельствуют обе карты – и для среднего уровня, и для рассеяния.

Для построения контрольной -карты средних значений в определенные промежутки времени берутся мгновенные выборки – подгруппы (обычно объемом n от 3 до 10 единиц продукции) и определяется среднее значение показателя Х в t-й выборке:

(x_ti – результат i-го наблюдения в t-й мгновенной выборке), которое и откладывается на карте.

Параметры технологического процесса μ₀ и σ могут быть известны заранее из технических условий или оцениваются в ходе процесса. В последнем случае если, например, взято m мгновенных выборок, то оценка x среднего значения уровня настройки μ₀ (средняя линия карты CL – Center Line) определяется по формуле

(5.2)

Рассеяние процесса можно оценить через размах мгновенной выборки R:

R_t = x_tmax – x_tmin (5.3)

среднее значение размаха

(5.4)

тогда контрольные границы карты (верхняя – UCL – Upper Control Limit и нижняя – LCL – Lower Control Limit)

. (5.5)

(А₂ – табличный коэффициент, определяемый в зависимости от объема мгновенной выборки n, значения этого и других, используемых при построении контрольных карт коэффициентов, приведены в таблице на стр. 56; коэффициент А₁ используется при известной дисперсии процесса).

Для построения карты размахов (R-карты) значения размахов мгновенной выборки откладываются по формуле (5.3). Положение контрольных границ определяются с помощью распределения размахов, квантили которого табулированы. На практике при использовании правила «трех сигма» контрольная граница определяется с помощью данных таблиц: LCL = D₃ и UCL = D₄ (коэффициенты D₃ и D₄ определяются по табл. на стр. 56; коэффициенты D₁ и D₂ используются при известной дисперсии процесса). При n < 7 нижние контрольные границы этих карт нулевые (чтобы исключить физически невозможные отрицательные значения, получающиеся по соответствующим зависимостям).

Показатель качества изделия должен находиться в некоторых заранее установленных границах – в пределах допуска. Для определения того, способен ли технологический процесс выпускать изделия, имеющие показатели качества в пределах допуска, используются индексы воспроизводимости.

Индекс воспроизводимости – безразмерная величина, показывающая связь между характеристиками технологического процесса и допуском. Пусть USL и LSL – соответственно верхняя и нижняя границы поля допуска, а σ – среднеквадратичное отклонение показателя качества в технологическом процессе. Тогда, если показатель имеет нормальное распределение и его среднее значение находится в середине поля допуска, индекс воспроизводимости Cp определяется по формуле

(5.6)

где при контроле технологического процесса с помощью карт Шухарта в качестве несмещенной оценки стандартного отклонения принимается величина

σ = / d, (5.7)

коэффициент d определяется по таблице на стр. 56 в зависимости от объема выборки.

В этих условиях при Cp = 1 вероятность брака теоретически составляет 0,27 %; при этом доля несоответствующих изделий составит 27/10000 = 2700 изделий на миллион, т. е. 2700 ppm (ppm – parts per million – единица измерения уровня несоответствий). Стандарт рекомендует в качестве минимально приемлемого значения Cp = 1,33 (при этом дефектность составит 63 ppm). При Cp = 1,67 уровень несоответствий составит 6 ppm, а при Cp = 2, когда поле допуска вдвое шире диапазона рассеяния технологического процесса, – 2 изделия на миллиард.

При одностороннем допуске вместо формулы (5.6) используют соответственно верхний индекс воспроизводимости

(5.8)

( – средний уровень настройки процесса), или нижний индекс воспроизводимости

(5.9)

Индекс воспроизводимости (5.6) предполагает точное центрирование процесса – совпадение среднего значения ( с целевым уровнем μ. Для учета расхождения между этими характеристиками вводится индекс центрированности k:

k = 2| μ – | / (USL – LSL); (5.10)

при точном центрировании k = 0, при совпадении среднего уровня с одной из границ поля допуска k=1.

Индекс работоспособности процесса (иногда называется индексом настроенности или налаженности)

Cpk = Cp (1 – k) (5.11)

не превышает индекса воспроизводимости.

Индекс работоспособности может быть записан в виде

Cpk = min (Cpu, Cpl ). (5.12)

Рассмотренные показатели применимы для оценки возможностей процесса в том случае, если с использованием контрольных карт подтверждена статистическая управляемость процесса. Для индивидуальных наблюдений дополнительно необходимо убедиться в нормальности распределения контролируемого показателя.

Если же стабильность (статистическая управляемость) процесса не подтверждена, то для оценки возможностей процесса используются индексы пригодности, определяемые по аналогии, но через оценку стандартного отклонения объединенной выборки

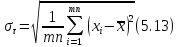
n – объем мгновенной выборки (подгруппы), m – количество подгрупп, mn – объем объединенной выборки:

Ppk = min (Ppu, Ppl ). (5.17)

Таблица коэффициентов для построения контрольных карт

ЗАДАНИЕ

Контролируется толщина лакового покрытия на изделии. Получены данные по 12 выборкам по три изделия в каждой. Построить карты Шухарта для средних значений и размахов. Является ли процесс стабильным? Оценить воспроизводимость процесса, если допуск на толщину покрытия лежит в пределах от 6 до 9 единиц.

1) Вычислить среднее значение и размах в каждой выборке.

2) Определить положение центральных линий карт средних значений и размахов.

3) Используя таблицу на стр. 56, найти положение контрольных границ карт средних значений и размахов.

4) Построить карты.

5) Дать заключение о стабильности процесса.

6) Найти оценку стандартного отклонения процесса через средний размах.

7) Вычислить индексы воспроизводимости и работоспособности процесса.

8) Дать заключение о воспроизводимости и центрированности процесса; расчет оформить в соответствии с образцом по рис. 5.1.

Рис. 5.1. Образец оформления рабочего листа при построении карт средних и размахов

5.2. Анализ чувствительности контрольной карты

Проанализируем, насколько чувствительны карты Шухарта к возможным нарушениям технологического процесса. При анализе чувствительности контрольных карт используется специальная характеристика, называемая средней длиной серий, – это среднее значение числа мгновенных выборок, взятых от момента нарушения процесса до момента обнаружения этого нарушения.

Предположим, что произошел сдвиг (смещение) уровня настройки процесса на величину . Как скоро -карта отреагирует на это нарушение? Сколько в среднем надо взять выборок, начиная с момента нарушения, чтобы среднее значение, откладываемое на карте, вышло за контрольные границы, показав тем самым, что технологический процесс вышел из-под контроля?

Средняя длина серий -карты может быть найдена по формуле

При = 0 смещения нет, Lх(0) = 1/, где – вероятность ложной тревоги. Например, при = 0,005 возможен в среднем один ложный сигнал на 200 выборок.

ЗАДАНИЕ

Проанализировать зависимость средней длины серий от смещения среднего уровня процесса (= 0 … 2,5) при объемах мгновенных выборок n = 3 и n = 5 на уровне значимости 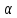= 0,0027 (соответствующем правилу «трех сигма»); расчет оформить в соответствии с образцом по рис. 5.2 (расчет СДС при n = 3 проведен непосредственно по формуле (5.18), при n = 5 – с вычислением промежуточных результатов).

Рис. 5.2. Образец оформления рабочего листа при анализе чувствительности карты к нарушению процесса

5.3. Карты средних и стандартных отклонений

Для оценки технологического рассеяния σ может быть использовано стандартное отклонение; вычисляется несмещенная оценка дисперсии каждой мгновенной выборки:

и среднее стандартное отклонение (определяющее положение центральной линии карты стандартных отклонений):

Величина является смещенной оценкой σ, несмещенная оценка

При использовании оценки стандартного отклонения (5.21), границы карты средних значений определяются по формуле

На карте стандартных отклонений откладываются значения S_t (из формулы (5.19)); контрольные границы карты при неизвестном значении σ соответственно LCL = В₃ и UCL = В₄. При n < 6 нижние контрольные границы этих карт нулевые: LCL = 0.

При анализе воспроизводимости процесса по формулам (5.6) – (5.9) используется оценка стандартного отклонения (5.21).

ЗАДАНИЕ

Контролировался вес упаковки продукта на автоматической линии, допуск 50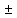0 10:

1) Вычислить среднее значение и стандартное отклонение в каждой выборке.

2) Определить положение центральных линий карт средних значений и стандартных отклонений.

3) Используя таблицу на стр. 56, найти положение контрольных границ карт средних значений и стандартных отклонений.

4) Построить карты.

5) Дать заключение о стабильности процесса.

6) Найти оценку стандартного отклонения процесса через среднее стандартное отклонение для объединенной выборки.

7) Вычислить индексы воспроизводимости и пригодности процесса.

8) Дать заключение о воспроизводимости процесса; расчет оформить в соответствии с образцом по рис. 5.3.