
Архив С / 6 семестр / Сист анализ / shpor
.docx|
1.сис анализ в совр исследований
В рамках системных исследований развиваются такие интеграционные науки, как: кибернетика, исследование операций, системотехника, системный анализ, искуственный интеллект и другие. Системный анализ разрабатывает системную методологию решения сложных прикладных проблем, опираясь на принципы системного подхода и общей теории систем, развития и методологически обобщая концептуальный (идейный) и математический аппарат кибернетики, исследования операций и системотехники. Системный анализ представляет собой новое научное направление интеграционного типа, которое разрабатывает системную методологию принятия решений и занимает определенное место в структуре современных системных исследований.
Рис.1.1 — Системный анализ
|
2. сис описание задачи оптимизации
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. При постановке задачи оптимизации необходимо: 1. Наличие объекта оптимизации и цели оптимизации. 2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы - управляющими воздействиями. 3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий. 4. Учет ограничений. Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод ). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой-критерием оптимальности. Принято различать задачи статической оптимизации для процессов, протекающих в установившихся режимах, и задачи динамической оптимизации. В первом случае решаются вопросы создания и реализации оптимальной модели процесса, во втором -задачи создания и реализации системы оптимального управления процессом при неустановившихся режимах эксплуатации.
|
3.сис анализ транспортных моделей. М. потенциалов Системный подход как метод познания транспорта представляет собой основу науки о транспортной системе, целью которой является обеспечение целостного, всестороннего подхода к решению сложных проблем развития и эксплуатации транспорта Метод потенциалов В методе потенциалов строке i и столбцу j транспортной таблицы ставятся в соответствие числа ui и j. Для каждой базиснойпеременной хij текущего решения потенциалы ui и j должны удовлетворять уравнению ui + j =cij. Эти уравнения приводят к системе, состоящей из т+п-1 уравнений (поскольку всего имеется т+п-1 базисных переменных), в которых фигурируют т+п неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из нихпроизвольное значение (обычно u1 полагается равным нулю) и затем решая систему из m+п-1 уравнений относительно m+n-1 остальных потенциалов. Уравнения ui+j=cij, используемые
для нахождения потенциалов, имеют
настолько простую структуру, что на
самом деле их не нужно записывать в
явном виде. Обычно гораздо проще
определять потенциалы непосредственно
из транспортной таблицы, заметив,
что ui строки i и j столбца j прибавляются
к cij,если
на пересечении строки i и
столбца j находится базисная переменная xij.Определив ui и j, можно
вычислить Как только решение получено, оценки для небазисных переменных хpqопределяются соотношением
Очевидно,
что цена цикла pq =
- Величины Для
включения в базис выбирается небазисная
переменная, имеющая самую
большую положительную оценку Для определения переменной, выводимой из базиса, строим замкнутый цикл, соответствующий вводимой в базис переменной Переменная, выводимая из базиса, выбирается из находящихся на изломах цикла переменных, помеченных знаком ‘-‘. Выводимой из базиса переменной становится та, которая имеет наименьшее значение, поскольку именно она раньше всех достигнет нуля, и любое дальнейшее уменьшение делает ее отрицательной Оптимальный
план получен, если все |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5. Решение транспортных задач методом Фогеля Данный метод состоит в следующем:
Если клеток с минимальным тарифом несколько, то заполняем ту из них, которой соответствует наибольшая разность. Если в строке/столбце две клетки с одинаковыми и минимальными значениями тарифов, то берем именно их. Затем повторяем все вышеописанные действия снова, только уже не учитывая заполненные клетки. И так до тех пор, пока не будет полностью найден опорный план.
|
6. Оптимизация назначений максимальное и минимальное значение функции Линейное программирование (оптимизация) применяется в оптимизационных моделях в случае поиска экстремума целевой функции Z? линейно зависящей от параметров c и x:
Эти ограничения называются условиями неотрицательности. Если все ограничения заданы в виде строгих неравенств, то данная форма называется канонической.
|
7. Динамическое программирование принцип оптимальности Беллмана Динамическая система – объем, способный развиваться во времени. Пространство состояний – множество всех возможных состояний динамической системы. Принцип оптимальности Беллмана: Каково бы ни было состояние системы S перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге + оптимальный выигрыш на всех последующих шагах был максимальным. Основное уравнение динамического программирования (уравнение Беллмана):
S`=
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8. Постановка задачи распределения инвестиций и алгоритм ее решения методом динамического программирования 1) Определение числа шагов равных количеству предприятий;2) Пусть S - количество средств, имеющихся в наличии перед данным шагом, и характеризующих состояние системы на каждом шаге;3) Управление на i -ом шаге выберем X, - количество средств, инвестируемых в i -ое предприятие;4) Выигрыш Pi (Xi) на i -ом шаге - это прибыль, которую приносит I -oe предприятие при инвестировании в него средств Xi. Если через выигрыш в целом обозначить общую прибыль W, то W = P1 (x1) + P2 (x2) + P3(x3);5) Если в наличии имеются средства в количестве S и в i -oe предприятие инвестируется X, то для дальнейшего инвестирования остается (S-X). Следовательно, функция перехода в новое состояние имеет вид: Fi (S-X) = S-X;6)На последнем шаге оптимальное управление соответствует количеству средств, имеющихся в наличии, а выигрыш равен доходу, приносимым последним предприятием: Xi (S) = S. Wi (S) = Pi (S);7) Согласно принципу оптимальности Беллмана, управление на каждом шаге нужно выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге. Основное функциональное управление примет вид: Wi (S) = maxx<=s {Pi (X) + Wi+1 (S - X)}
|
9. Постановка задачи о бинарном рюкзаке и алгоритм ее решения методом динамического программирования. Постановка задачи: Имеется рюкзак, который может вместить предметы с общим весом не более заданного. Предлагается ряд предметов фиксированного веса и фиксированной стоимости (ценности).Задача состоит в том, чтоб уложить как можно большее число ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена. Требуется выбрать из заданного множества предметов набор с мах суммарной стоимостью при одновременном соблюдении ограничения на суммарный вес найденного набора. Выбрав набор с мах ценностью задача будет решена. Имеется: аi– вес; сi– ценность (стоимость); Y – вместимость; хi – количество предметов. Алгоритм: 1) Пусть функция Fk(Yi) – максимальная стоимость, которую нужно найти. Допустим, мы уже нашли предмет, весом меньше полной вместимости Yi. 2) Проверим стоит ли его брать. Если его взять, то вес станет Y- Yi , тогда Fk(Yi)= Fk(Y-Yi)+ сi . Если не брать предмет, то вес остается тем же, и из двух вариантов выбирается тот, который дает наибольший результат. 3)
Математическая модель задачи: С(Х)=
4) Составление основного функционального уравнения (функция Беллмана). Fk(Yi) = max{CkXk+Fk-1(yi-ak *xk)}, xk≤Y/ ak.
|
10. Постановка задачи о рюкзаке с неограниченным количеством элементов и алгоритм ее решения методом динамического программирования. Постановка задачи: Имеется рюкзак, который может вместить предметы N различных типов (количество предметов каждого типа не ограничено). Требуется определить максимальную стоимость предмета вес, которого не превышает W. Задача состоит в том, чтоб уложить как можно большее число ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена. Имеется: W – вместимость рюкзака; n – количество i-типа предметов; ωi– вес i-типа предмета; рi– стоимость i-типа предмета; ki – количество экземпляров i-типа предмета. Задачу можно решить с помощью «дерева решений». В каждом кружочке показан вес предмета, корень дерева - нулевой вес, то есть когда рюкзак пуст. Первый предмет можно выбрать четырьмя способами, второй - тремя, третий - двумя, а дальше можем взять только один оставшийся предмет. Выбрав набор с мах весом предмета, задача будет решена.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11. Постановка задачи о замене оборудования и алгоритм ее решения методом динамического программирования. Задача: Для каждого года в плановом периоде надо решить – сохранять имеющуюся в этот момент оборудования или заменить его, чтобы суммарная прибыль за весь плановый период была максимальной.Имеется: t – возраст оборудования, t=0,1,2…, где t=0 – новое оборудование, t=1 – оборудованию 1 год.R(t) – стоимость продукции, производимой за 1 год на оборудовании возраста t. C(t) – эксплуатационные затраты за 1 год на оборудовании возраста t.S(t) – остаточная стоимость оборудования возраста t.T- текущее время.Р(Т) – цена нового оборудования в году t.t0 – начальный возраст оборудования.N – длина планового периода. Пояснения: Введем функцию fn(t) – величину суммарной прибыли за последние n –лет планового периода. С помощью f1(t), f2(t),…, fn(t) – функций Беллмана ведется анализ задач динамического программирования. Очевидно, если мы сумеем вычислить fn(f0) и найти политику замен, то это и будет решение задач. Алгоритм: 1) определение числа шагов, равное числу лет, в течение которых эксплуатируется оборудование. 2) определение управлений. Сохранить оборудование: xi=0. Заменить оборудование: xi=1. 3) определение функции выигрыша на i-м шаге. R(t)-C(t) –сохранить, S(t)-P+R(0) –C(0)+ fn(1) - заменить оборудование. 4) Составление основного функционального уравнения (функция Беллмана). Для первого шага: F1(t)=max(R(t)-C(t),S(t)-P+R(0) –C(0)). Для последующих шагов: Fj(t)=max(R(t)-C(t)-fj+1(t+1),S(t)-P+R(0) –C(0)+fj+1(1)), где j =2,3..,n. Решение задачи найдено.
|
12. Принятие решений на основе расчета функции полезности. Если известны оценки альтернатив, веса критериев и, если решается задача на мах, т.е. чем выше оценка альтернативы, тем она более привлекательна, то для принятия оптимального решения нужно вычислить функции полезности каждой альтернативы. Fi=
Результат выбора решения является более рациональным (привлекательным), если его функция полезности максимальна.
|
13. Экспертные методы в процессе прогнозирования и разработки управленческих решений. Сущность экспертных методов заключается в построении рациональной процедуры интуитивно-логического мышления человека в сочетании с количественными методами обработки и анализа полученных результатов. При этом обобщенное мнение экспертов принимается как возможное решение проблемы. 1. Определение целей. Для сложных ситуаций применять дерево целей. 2. Экспертный прогноз. Экспертная информация содержит не только количественные, но и качественные оценки. 3. Сценарии ожидаемого развития ситуации. Наиболее часто для формирования сценария применяют метод мозговой атаки в сочетании со специальными приемами аналитической информации. 4. Генерирование альтернативных вариантов. Проведение экспертиз с использованием методов типа мозговой атаки, а также создание в сложных случаях автоматизированных систем генерирования альтернативных вариантов. 5. Определение рейтингов. Позволяют оценивать сравнительную надежность банков, страховых компаний и т.д. 6. Оценочные системы. Формируются при индивидуальных и коллективных сравнительных оценках объектов экспертизы для определения степени достижения цели. 7. Принятие коллективных решений. Методы экспертных оценок: 1)Коллективные работы экспертных групп(Мозговой атаки, Сценариев, Совещаний, Суда, Деловых игр, Дерева целей) 2)Индивидуального мнения экспертов (Дельфи, Интервью, Анкетного опроса)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
15.Методы определения согласованности и экспертов В связи с природой данных, которые являются результатами экспертных оценок (обычно баллы), для их анализа обычно используются ранговые (непараметрические) методы. Для того чтобы оценить согласованность мнений двух экспертов при их оценке ряда признаков можно воспользоваться коэффициентом корреляции Спирмена или коэффициентом корреляции Кендалла. Smax=1/2*nm2(n2-1), где m- число экспертов в группе, n- число факторов. Величина коэффициентов конкордации меняется в пределах от 0 до 1. Если 1- все эксперты дали одинаковые оценки, если 0- связи между оценками не существует. Если мнения экспертов полностью противоположны, коэффициент конкордации равен нулю (W = 0), а коэффициент корреляции в этом случае будет равен -1. Коэф. КонкордацииW позволит оценить насколько согласованны между собой ряды:W=S/Smax. В случае если экспертов не два, а более (например, при выяснении согласованности мнений группы экспертов), используется дисперсионный коэффициент конкордации:V=(12*S)/(m2*(n3-n)), V<0.2-0.4 –слабое согласование; V>0.6-0.8- сильное согласование. Rij - ранг j-го объекта, который присвоен ему i-ым экспертом. Дисперсионный коэффициент конкордации рассчитывают по матрице ранжировок n объектов группой из m экспертов, где rij - ранг, присвоенный j-ым экспертом i-ому объекту. Метод Средней точки. Пусть f(a1) оценка первого альтернативного вар. Знач, а f(a2)- второго.Расчет f(a1)+f(a2)/2=f(a3) – третий альтернативный вариант.F(a1) и f(a2)-могут быть полярными.Даже экспертом указывается альтернативный вариант а4, значение которого расположено между f(a1) и f(a3) и а5 между f(a1) и f(a2).Завершается, когда определ. Предпочтит. Всех вариантов.
|
16. метод Паттерн Это разновидность экспертных методов,позволяет анализировать и ранжировать по степени важности сведения в любой области деятельности. дерево целей метода Паттерн-Методика PATTERN основана на принципе деления сложной проблемы на более мелкие проблемы до тех пор, пока каждая подпроблема не сможет быть всесторонне (разные критерии) и надежно количественно оценена экспертами (метод экспертных оценок).разработка начинается с составления сценария. Д.ц состоит из 8 уровней Каждый уровень имеет определенное кол-во элементов О-нац.идеи(1),А-мероприятия(3), В-задачи(6), С-задания(46), D-принципы систем, Е-функциональные подсистемы, F-конструкции функциональных подсистем,G-технические проблемы.Для каждого уровня дерева целей вводится ряд критериев. С помощью экспертной оценки определяются веса критериев и коэффициенты значимости (важности), характеризующие важность вклада целей в обеспечение критериев. Сумма коэффициентов относительной важности для каждого уровня иерархии принимается равной единице. Главное достоинство методики состоит в том, что в ней определены классы критериев оценки: + относительной важности; + состояния разработки ("состояние-срок"); + взаимной полезности. Методика PATTERN применяется: + при планировании научно-исследовательских и опытно-конструкторских разработок для достижения целей в условиях неопределенности (т.е. в сложных, противоречивых системах); + при выделении функциональных подсистем; + в принятии решений с помощью компьютерных программ; этапы метода: + разработка "сценария", представляющего собой прогноз политической картины мира на прогнозируемый период; + разработка прогноза развития науки и техники (который может быть и составной частью "сценария"); + разработка "дерева целей"; + оценка составляющих "дерева целей" путем определения коэффициентов относительной важности, состояния разработки и сроков, взаимной полезности; + обработка результатов оценки (подсчет суммарных коэффициентов с использованием специально разработанной процедуры обработки результатов на ЭВМ) и представление результатов лицам, принимающим решения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
17Методы групповой экспертной оценки: При использовании экспертных оценок обычно предполагается, что мнение группы экспертов надежнее, чем мнение отдельного эксперта. М.комиссий это открытая комиссия по обсуждаемой проблеме, для выработки единого мнения экспертов.коллективное мнение определяется в результате открытого или тайного голосования.+ рост информированности экспертов, обратная связь. -дискуссия принимает вид полемики,различная активность экспертов Экспертиза по методу суда-аналогия с судебным процессом.состав экспертов делится на 2 гр:1.сторонники рассматриваемой темы, выступают в качестве защиты.2.противники, пытаются выявить отриц стороны.возможна 3 сторона-выносит окончательные решения М.прогнозного графа.несколько туров.1.составляется список промежуточных целей.эсперты указывают специалистов,способных оценить возможность реализации каждой из указанных или промежут и конечных целей. 2. Анализу подвергаются уже не конечная цель, а промежут цели сформулированные экспертами на 1 туре. Послудующие торы аналогичны 2.процедура заканчивается на том туре,когда больше не требуется доп анализов и детализации. М.сценариев. сценарий означает сюжетную схему т.е. заранее подготовленный план осуществления чего-либо. При подготовке сценария внимание обращают, а критические точки ветвления. Т.е точки в которых малые воздействия оказывают заметное влияние на результат. Каждыйсценарий может быть реализован в нескольких вариантах. Разработка сценариев способствует предвидению потенциальной опасности, в которой сопряжены варианты управленческих воздействий и неблагоприятное развитие событий
|
18.Метод "Дельфи" Это метод быстрого поиска решений, при котором эксперты не контактируют друг с другом, а решения принимаются на основе анонимного анкетирования. Применение данного метода предполагает несколько этапов анкетирования. После обработки и анализа результатов анкетирования принимается коллективное решение о перспективности идеи. Позволяет избежать группового влияния, возникающее при совместной работе и состоящее в приспособлении к мнению большинства, даёт возможность проводить опрос экстерриториально, не собирая экспертов в одном месте (например, посредством электронной почты). Особенности: 1)Заочность (анонимность). Участники экспертной группы неизвестны друг другу и их взаимодействие в процессе опроса полностью исключено. 2) Многоуровневость 3)Статистическая обработка результатов опроса и формирование группового мнения после каждого этапа (уровня). Критерием окончания процесса поиска решения, как правило, служит «близость» мнений экспертов. Метод Дельфи - это систематический способ обобщения оценок экспертов.
|
14. Метод ранжирования мнений экспертов. Эксперту предлагается присвоить числовые ранги каждому из приведенных в анкете факторов. Ранг =1 присваивается наиболее важному, по мнению эксперта, фактору, ранг =2- присваивается следующему по важности фактору. Порядковая шкала получаемая в результате ранжирования, должна удовлетворять условию равенства числа рангов N числу ранжированных элементов. Стандартизованные или связанные (одинаковые) Rсвязприменяются когда сложно опрделить границу между элементами.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
20. Охарактеризуйте критериев пессимизма - оптимизма(гурвица) и критериев минимального риска (севиджа). Критерий Гурвица – критерий обобщенного максимума, или пессимизма-оптимизма.Представляется логичным, что при выборе решения вместо двух крайностей в оценке ситуации придерживаться некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего, благоприятного поведения природы.
Согласно
этому подходу для
каждого решения необходимо определить
линейную комбинацию min и max выигрыша
и взять ту стратегию, для которой эта
величина окажется наибольшей.Этот
критерий обеспечивает промежуточное
решение Аi между
крайним оптимизмом и крайним пессимизмом,
которое определяется по принципу: Число (a=1-y)- степень оптимизма, удовлетворяет условию 0≤ a≤ 1 и выбирается из субъективных соображений, особенностей среды, здравого смысла, исходя из опыта ЛПР, его отношения к риску и т.п. На выбор значения степени оптимизма оказывает влияние мера ответственности: чем серьезнее последствия ошибочных решений, тем больше желание принимающего решение застраховаться, то есть степень оптимизма ближе к нулю. Для каждой строки рассчитывается среднее взвешенное (с учетом выбранного значенияy) наименьшего и наибольшего результатов, после чего выбирается строка с максимальным значением. Приy=0 имеем критерий крайнего оптимизма, т.е. отражает позицию азартного игрока, ожидающего наиболее благоприятное состояние среды. Приy=1 критерий Гурвица превращается в критерий крайнего пессимизма Вальда. Если 0<y<1, то имеем промежуточное отношение ЛПР к возможным рискам. При желании подстраховаться в данной ситуацииy принимают близким к единице. Выбор значенияy субъективен, а, следовательно, субъективен и выбор решения, что совершенно неизбежно в условиях неопределенности. Чем опаснее ситуация, тем больше ЛПР стремится застраховать себя от возможных рисков, тем ближеy к 0. А чем менее он азартен, тем y ближе к 1. Оптимальная по Гурвицу стратегия должна гарантировать статистику больший выигрыш по сравнению с выигрышем, принимаемым статистиком интуитивно или исходя из опыта. Применение критерия Гурвица оправданно, если ситуация, в которой принимается решение, характеризуется признаками: - вероятности состояний природы неизвестны; - необходимо считаться с наихудшим из возможных вариантов; - решение реализуется малое количество решений; - допускается некоторый риск. Пример:Для
применения критерия
Гурвица нужно
знать значение вероятностиy .
Пусть, например,y=0,9 .
Это означает, что событие «наименьший
возможный выигрыш статистикаA »
желаем сделать более правдоподобным
(y близко
к единице), то есть страхуемся от
неблагоприятных ситуаций в игре.
Тогда Из последнего столбца таблицы видно, что максимальное значениеhi равно (–7,2) и соответствует чистой стратегииA3 ; она и будет оптимальной по критерию Гурвица. Анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет глубже исследовать суть явления и выбрать наиболее обоснованное управленческое решение. В качестве оптимальной на основании совокупных исследований берется та стратегия, которая чаще других называлась оптимальной по всем критериям. Критерий Сэвиджа (минимаксного риска) – это критерий минимаксного риска, минимизации «сожалений». Этот критерий, как критерий Вальда, является максимально осторожным и пессимистическим.На практике, выбирая одно из возможных решений, часто останавливаются на том, осуществление которого приведет к наименее тяжелым последствиям, если выбор окажется ошибочным. По принципу Сэвиджа каждое решение характеризуется величиной дополнительных потерь, которые возникают при реализации этого решения, по сравнению с реализацией решения, правильного при данном состоянии природы. Он особенно удобен для экономических задач и часто применяется для выбора решений в играх человека с природой. Естественно, что правильное решение не влечет за собой никаких дополнительных потерь, и их величина равна нулю. |
При выборе решения, наилучшим образом соответствующего различным состояниям природы, следует принимать во внимание только эти дополнительные потери, которые по существу, будут являться следствием ошибок выбора. Для решения задачи строится так называемая «матрица рисков», элементы которой показывают, какой убыток понесет игрок (ЛПР) в результате выбора неоптимального варианта решения. Риском игрокаrij при выборе стратегии в условиях (состояниях) природы Пjназывается разность между максимальным выигрышем, который можно получить в этих условиях, и выигрышем, который получит игрок в тех же условиях, применяя стратегию. В критерии Сэвиджа пессимизм проявляется по-другому: худшим считается не минимальный выигрыш, а максимальная потеря выигрыша по сравнению с тем, что можно было бы достичь в данных условиях (максимальный риск). Критерий Сэвиджа ориентируется не на результат, а на риск (потери или штрафы)rij . В
качестве оптимальной выбирается
стратегия, при которой величина потерь
в наихудших условиях минимальна. Критерий
Сэвиджа рекомендует выбирать в
качестве оптимальной ту стратегию,
которая минимизирует максимальный
риск: Пример. Для задачи «Поставщик» мини/макс риска достигается сразу при двух стратегиях А2 и А3:
Решение.Ориентируемся на самые неблагоприятные состояния «природы». Вычислим риски статистика А.Для первого столбца:
Для
второго столбца: Для
третьего столбца: Запишем матрицу
рисков Определим в каждой строке наибольшее число – наибольший риск статистикаA , если он применяет стратегиюAi , а природа меняет свои состояния П1, П2 , . Дополним матрицу рисков последним столбцом «наибольшие риски».
Найдем
наименьший риск: Значит,
оптимальной стратегией по критерию
Сэвиджа является стратегия
|
19.Принятие решении в условиях неопределенности Прежде всего отметим принципиальное различие между стохастическими факторами, приводящими к принятию решения в условиях рыска, и неопределенными факторами, приводящими к принятию решения в условиях неопределенности. И те, и другие приводят к разбросу возможных исходов результатов управления. Но стохастические факторы полностью описываются известной стохастической информацией, эта информация и позволяет выбрать лучшее в среднем решение. Применительно к неопределенным факторам подобная информация отсутствует. Неопределенность может быть вызвана либо противодействием разумного противника, либо недостаточной осведомленностью об условиях, в которых осуществляется выбор решения. Принятие решений в условиях разумного противодействия является объектом исследования теории игр. Принципы выбора решений при наличии недостаточной осведомленности относительно условий, в которых осуществляется выбор принято называть «играми с природой».
В
терминах «игр с природой» задача
принятия решений может быть сформулирована
следующим образом. Пусть лицо,
принимающее решение, может выбрать
один из т
возможных вариантов своих решений:
Теория статистических решений предлагает несколько критериев оптимальности выбора решений. Выбор того или иного критерия неформализуем, он осуществляется человеком, принимающим решения, субъективно, исходя из его опыта, интуиции и т. д. Критерий минимакса
Этим
критерием предписывается оценивать
системы по максимальному значению
эффективности и выбирать в качестве
оптимального решения обследующую
эффективность с наибольшим из
максимумов:
Критерий
Вальда.
В каждой строчке матрицы выбираем
минимальную оценку. Оптимальному
решению соответствует такое решение,
которому соответствует максимум этого
минимума, т. е.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
21. методы выбора альтернатив в условиях риска( дерево решений) Дерево решений. Следующий метод, применяемый для принятия решений в условиях риска, носит название дерева решений. Его применяют тогда, когда необходимо принимать последовательный ряд решений. Дерево решений – графический метод, позволяющий увязать точки принятия решения,возможные стратегии Ai, их последствия Ei,j с возможными факторами, условиями внешней среды. Построение дерева решений начинается с более раннего решения, затем изображаются возможные действия и последствия каждого действия (событие), затем снова принимается решение (выбор направления действия) и т. д., до тех пор, пока все логические последствия результатов не будут исчерпаны. Дерево решений строится с помощью пяти элементов: 1.Момент принятия решения. 2.Точка возникновения события. 3.Связь между решениями и событиями. 4.Вероятность наступления события (сумма вероятностей в каждой точке должна быть равна 1). 5.Ожидаемое значение (последствия) – количественное выражение каждой альтернативы, расположенное в конце ветви. Простейшее решение представляет собой выбор из двух вариантов – «Да» или «Нет» .
Пример 1. Формула Ж. Поля Гетти «Как стать богатым»:«Вставай рано»; «Работай усердно»; «Найдешь нефть!». Моделирование последовательности решений (рис. 21): 1.Решение: Нужно сделать выбор между тем, чтобы «Вставать рано» или «Спать допоздна» – простейший выбор. 2.Решение: Нужно сделать выбор между тем, чтобы «Работать усердно» или «Спустя рукава» – простейший выбор. 3.Событие: «Найдешь нефть», происходит с определенной вероятностью, зависящей от последовательности принимаемых решений.
|
22 пассивный метод поиска минимума функции одной переменной Метод оптимизации называется пассивным, когда все точки xi ,i = 1,N, вычислений характеристик задачи (в данном слу- чае значений целевой функции) выбираются одновременно до начала вычислений. Если N четное, т.е.N = 2l,l = 1,2,", то наилучшее (в смысле максимального уменьшения длины отрезка локализации) размещение точек xi , i = 1, N , получается разбиением их на равноотстоящие ε-пары,т.е. x 2 j −1 =( (a + b – a)/N2+1)* j – ε/2 , x 2 j =(( a + b – a)/N2+1)* j + ε/2 ,j = 1,N 2, (4.1) где ε − некоторое малое положительное число. При этом LN=((b-a)/N2+1) + ε/2=( L0/l+12)+ ε Если N нечетное, т.е. N = 2l +1,l = 1,2,", то наилучшим является равномерное распределение точек, т.е. xi = a + ((b – a)/N+1) i, i =1, N При этом LN= 2((b – a)/N+1)- (L0 / l +1) Нетрудно заметить, что использование нечетного числа точек при пассивном методе поиска неэффективно. После определения точек xi , i= 1, N , вычисляются значе- ния функции f (xi ) . Пусть f (xk )’ i =1, N ‘= min f (xi ). Тогда, полагая x0 = a, xN +1 = b, определяется итоговый отрезок локализации ∆N = [xk −1,xk +1] . Точка xk принимается за аппроксимацию (оценку) точки минимума x , значение функцииf (xk )− за оценку f * = f (x*) , т.е.x*= xk , f*= f(xk ). Пример. Определить с помощью пассивного поиска ми- нимум функции f (x) = x+ 1/x , заданной на отрезке ∆ = [0,2]: а) при N=6,ε=0,1; б) приN=7. Решение. а) N=6,ε =0,1. Определяем пары точек x2j−1, x2j с помощью соотношения (4.1): x2j−1 = 0 +((2-0i)/3+1)-0.1/2=0.5j-0.05, j = 1,3; x2j = 0 + ((2 − 0 j)/3+1) + 0.1/2 = 0,5 j + 0,05, j = 1,3. Результаты вычислений x и f (x) заносим в табл. 4.1. Таблица 4.1 Номер 1 2 3 4 5 6 отсчета x 0,45 0,55 0,95 1,05 1,45 1,55 f (x) 2,67 2,37 2,0026 2,0024 2,14 2,20 Поскольку f (x4 )= min’ i =1,6 ‘ f (xi ) , то полагаем ∆6=[x3,x5]= =[0,95; 1,45], x x4 = 1,05, f * f (x4 )= 2,0024. Ответ: ∆6 = [0,95; 1,45] , x* 1,05, f * 2,0024.
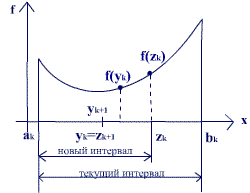
25. Численный метод оптимизации функции одной переменной – метод «золотого сечения»
Тебуется
найти безусловный минимум функции
f(x) одной переменной, т.е. такую точку При построении конкретного метода одномерной оптимизации, работающего по принципу сокращения интервала неопределенности, следует определиться с правилом выбора на каждой итерации двух внутренних точек, при этом желательно, чтобы одна из них всегда использовалась в качестве внутренней для следующего интервала. В этом случае число вычислений функции сократится вдвое, и новая итерация потребует расчета только одного нового значения функции. В методе золотого сечения в качестве внутренних точек выбираются точки золотого сечения. Определение. Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей. Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм основан на анализе величин функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины. Алгоритм.
|
23 метод дихотомии(половинного деления) как метод оптимизации унимодальной функции Метод оптимизации называется активным, если точки х,, i = 1, N, вычислений характеристик задачи (в данном случае значений целевой функции) выбираются последовательно, с учетом информации, полученной на предыдущих шагах. Для активных (последовательных) методов поиска принято указывать в используемых обозначениях номер итерации с помощью надстрочного индекса в круглых скобках. В соответствии с этим отрезок локализации после ] итераций будет обозначаться А^( ]) = [a^(J), b^( J)]. алгоритм выполнения
для которой значение функции минимально Пример. Определить методом дихотомии минимум функцииf (x)= x4 − 6x2 +10 , заданной на отрезке∆=[1,3], приN=8,ε=0,1. Решение. В данном случае будут выполнены N/2=4 итерации. Результаты вычислений заносим в табл. 4.3. Таблица 4.3
Поскольку j=N/2=4, то вычисления завершаются. Точка минимума локализована на отрезке ∆8 = [1,594; 1,813] . На данном отрезке исследованы 4 точки:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
24 численный метод оптимизации функции одной переменной -метод Фибоначчи
числа Фибоначчи, определяемые следующим образом: F0 = F1 = 1,Fk = Fk −1 + Fk − 2 ,k = 2,3,.... Условием окончания вычислений является выполнение заданного количества вычислений N. Итак, алгоритм поиска минимума унимодальной функции методом Фибоначчи заключается в следующем. 1. Задается N, определяются числа ФибоначчиFk,k = 0,N +1, выбираетсяε из условия ε< b− a. FN+1 Полагается j=1. 2. На j-йитерации вычисляются
3 3. Проверяется условие окончания вычислений j = N −1. Если оно выполняется, то определяются итоговый отрезок локализации, оценки точки минимума x и величины минимума f * = f (x*) и вычисления завершаются. Если условие не выполняется, то полагается j=j+1 и осуществляется переход к п.2. Примечание. Наj-й,j>1, итерации вычисляется только та точкаxi( j ) ,i = 1,2, которая не была определена на предыдущей итерации. Отметим, что оценкой точки минимума x* является та из точекxi( N −1) ,i = 1,2, которая осталась внутри итогового отрезка локализации ∆N .
|
1. Задать
начальный интервал
неопределенности
б) если
6. Вычислить
|
26. Градиентный метод оптимизации – метод с дроблением шага В этом варианте градиентного метода величина шага αn на каждой итерации выбирается из условия выполнения неравенства
где ε ∈ (0, 1) — некоторая заранее выбранная константа. Условие (11) гарантирует (если, конечно, такие αn удастся найти), что получающаяся последовательность будет релаксационной. Процедуру нахождения такого αn обычно оформляют так. Выбирается число δ ∈ (0, 1) и некоторый начальный шаг α0. Теперь для каждого n полагают αn = α0 и делают шаг градиентного метода. Если с таким αn условие (11) выполняется, то переходят к следующему n. Если же (11) не выполняется, то умножают αn на δ ("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство
не будет выполняться.
27.Градиентный метод оптимизации – метод наискорейшего спуска. В
данном случае на каждой интеграции
шаг
где
Алгоритм метода: 1.Задаются
2.
определяется
3.вычисляются
4.проверяется
условие окончания вычислений
Если
оно выполняется, то полагается
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
28. Градиентный метод оптимизации – метод Ньютона Метод
Ньютона так же как и градиентные
методы, относится к методам спуска,
т.е. предназначены для численного
решения задач безусловной минимизации.
Метод Ньютона основан на идее замены
минимизируемой функции f(x)
в окрестности точки
Суть
метода: в методе Ньютона очередная
точка
Алгоритм метода: 1.Задаются
Задаются
2.вычисляется
3.определяется
4.вычисляются
5.проверяется
условие окончания вычислений
|
32Понятие лингвистической переменной. Метод Мамдани При формировании базы нечетких правил используются лингвистические переменные, с помощью которых может быть построена система правил след.типа: ЕСЛИ b1это А1 Иb2 это А2 ТО b3 это А3 или ЕСЛИ b1это А1 ИЛИb2 это А2 ТО b3 это А3 Где bi – лингвистические переменные;Aj – нечеткие множества, соответствующие базовым или модифицированным с помощью процедур G значениям лингвистической переменной. В данной записи переменные b1иb2 относящиеся к условиям правил, называются входными переменными, а b3из заключения – выходной лингвистической переменной. Алгоритм нечеткого вывода по Мамдани. ЕСЛИ b1это А1 Иb2 это А2 ТО b3 это А3 ЕСЛИ b1это В1 Иb2 это В2 ТО b3 это В3 Этап
1.
Фазификация входных переменных:
по фактическим точным значениям
входных переменных
Этап2. Нечеткий вывод состоит из двух действий – агрегирования предпосылок и активизации заключений правил. Сначала находятся степени истинности правил, в данном случае с использованием операции min, т.к. употребляются логические связки «И»: a1=min[μA1( a2=min[μB1( Затем определяются «усеченные» функции принадлежности для заключений правил: μ’A1(y)=min[a1,μA1( μ’B1(y)=min[a2,μB1( где
y Этап 3. Аккумуляция заключений нечетких правил. Найденные «усеченные» функции объединяются, в результате чего получается итоговое нечеткое множество для входной переменной с функцией принадлежности: μ(y)=max[μ’A1(y), μ’B1(y)] Этап 4. Дефазификация для нахождения, если это требуется, точного y0.
|
4.Алгоритм решения транспортной задачи при получении максимального значения функции Для решения задачи составляем матрицу рисков: для этого выбираем максимальный элемент (здесь 8), увеличиваем его на некоторое постоянное число (здесь 8+2 = 10), Предположим, что 10 – это есть наша желаемая прибыть, тогда вычитая из 10 все имеемые транспортные тарифы , то есть элементы матрицы исходной (А), получаем новую матрицу(В) –матрицу возможных потерь, матрицу рисков. А = В = 10 – 8 =2 7 9 6 3 6 5 8 4
8 3 1 4 7 4 5 2 6 Теперь для заданной матрицы решаем задачу на МИН, так как чем меньше риск – тем лучше. Пусть имеем задачу –составить оптимальный план распределения путевок в Париж 30 шт, Рим 90шт и Лондон 50 шт. Среди желающих поехать (Школьники, Студенты, Молодожены) . Опрос показал следующее распределение в Париж хотят 70, в Рим 60 и Лондон 30. Тогда составим таблицу,выбираем минимальную цену, вносим максимальную поставку, а далее решим одним из методов – здесь метод потенциалов и найдем оптимальный план f(x). Париж Рим Лондон N желающих поехать U Школьники 308/2 303/7 10/9 1 70 , /0 Студенты х/6 607/3 х/6 60, / -4 Молодожены х/5, х/8, 306/4, 30, / -5 Остаток х/0, х/0, 1/0 0, 10, /-9 N путевок 30 90 50 170/160+10 V 2 7 9 И тд Чтобы найти максимум функции, смотрим на матрицу А, исходные значения затрат умножаем на количество: f(х)= 240+90+10+420+180=940 Ответ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
29.Понятие нечеткого множества и операции над ними. Нечетким
мн-м С в Х наз-ся сов-ть пар вида (x, Справедливо
утверждение: «нечеткое множество
вполне описывается своей функцией
принадлежности». Обычные(четкие) мн-ва
составляют подкласс нечетких мн-в.
Для обычного мн-ва функция принадлежности
Операции над нечеткими множествами: 1.Объединением
нечетких множеств А и В в Х называется
нечеткое мн-во А
2.пересечением
нечетких мн-в А и В в Х называется
нечеткое мн-во
3.
дополнением нечеткого мн-ва А в Х
называется нечеткое мн-во
4.Разность
нечетких мн-в А и В в Х определяется
как нечеткое мн-во А-В с функцией
принадлежности вида
Декартово произведение А1*А2*….*Аn нечетких мн-в А1 в Х1 определяется как нечеткое мн-во А в декартовом произведении Х=Х1*Х2*….*Хn с функцией принадлежности вида
|
30.функции принадлежности элементов нечеткого множества их назначение и виды 1-Треугольная
функция
где
a,b,c
- некоторые числовые параметры,
упорядоченные отношением a≤b≤cи
принимающие произвольные действительные
значения. Функция принадлежности
порождает нормальное выпуклое
унимодальное нечеткое множество с
носителем (a,c),
границами (a,c)/ 2-
Функция принадлежности Гаусса
3- Сигмовидная функция
В зависимости от знака параметра a рассматриваемая ФП будет открыта или справа или слева, что позволит применять её при описании таких нечетких понятий, как «очень большой», «крайне отрицательно» и др.
|
31 нечеткие отношения. Понятия и принципы композиции нечетких отношений Нечеткие отношения Если элемент u под номером i находится в отношении R с элементом vс номерjм j, то записывают rij(ui,vj). Отношения можно представить в виде матрицы.
Таблицу
можно расписать иначе, в виде «суммы»,
где знак «+» будет означать лишь факт
принадлежности элемента к подмножеству
Композиция отношений В логике нечетких отношений произведение нечетких множеств моделирует знание-правило «если U, то V», т.е. моделирует отношение-продукцию U→V. R = U * Vвыполняет операцию U→V,S = V * W1 Композиция множеств позволяет дать ответ на вопрос: «Как определить отношение вида?» U * V→V * W1 В левой части имеем:rij = μR(ui,vj) В правой части имеем:sij = μS(vi,ϕj) Сущность операции свертки представляет собой классический алгоритм произведения матриц R→S P = R ° S P11=max P32=max
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


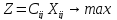 (min)
(min) Множество
на котором ищется экстремум целевой
функции, задается системой:
a11 x1 +
a12 x2 +
. . . +
a1nxn ≤
b1 ;
a21 x1 +
a22 x2 +
. . . + a2n xn ≤
b2 ;
.
. . . . . . . . . . . . . . . . . . . . . . . . . . .
am1 x1 +
am2 x2 +
. . . +
amn xn ≤
bm ;
x1 ≥
0, x2 ≥
0, . . . , xn ≥
0 .
Множество
на котором ищется экстремум целевой
функции, задается системой:
a11 x1 +
a12 x2 +
. . . +
a1nxn ≤
b1 ;
a21 x1 +
a22 x2 +
. . . + a2n xn ≤
b2 ;
.
. . . . . . . . . . . . . . . . . . . . . . . . . . .
am1 x1 +
am2 x2 +
. . . +
amn xn ≤
bm ;
x1 ≥
0, x2 ≥
0, . . . , xn ≥
0 . ,
где
-текущее
состояние системы
,
где
-текущее
состояние системы =
= -
функция
выигрыша при использовании управления
-
функция
выигрыша при использовании управления
 на i–ом
шаге
на i–ом
шаге -
следующее
состояние, в которое переходит система
под воздействием управления
-
следующее
состояние, в которое переходит система
под воздействием управления

 →max.
→max.
 ≤Y.
≤Y.
 ,
где i=1,2,..,n;
Wj
– вес критериев; Uij
– оценка i-й
альтернативы по j-му
критерию.
,
где i=1,2,..,n;
Wj
– вес критериев; Uij
– оценка i-й
альтернативы по j-му
критерию. 



 выбирается из условия минимума функции
f(x)
в направлении движения. Т.е.
выбирается из условия минимума функции
f(x)
в направлении движения. Т.е.
 ,
,


 ;
вычисляются
;
вычисляются
 полагается k=1
полагается k=1


 ,
,
 и вычисления завершаются.
и вычисления завершаются. квадратичной частью
квадратичной частью
 ee
разложения в ряд Тейлора
ee
разложения в ряд Тейлора

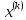 в последовательности
в последовательности
 …приближений
к точке минимума
…приближений
к точке минимума
 выбирается по правилу:
выбирается по правилу:
 ,
где
,
где
 -матрица,
обратная матрице А. Таким образом,
метод Ньютона является методом второго
порядка.
-матрица,
обратная матрице А. Таким образом,
метод Ньютона является методом второго
порядка.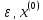 ;
вычисляются
;
вычисляются
 полагается k=1
полагается k=1

 ,
,

 .
Если оно выполняется, то полагается
.
Если оно выполняется, то полагается
 ,
,
 и вычисления завершаются.
и вычисления завершаются. ,
, (
( где
где
 – базовые пространства входных
переменных b1и
b2
соответственно) определяются степени
истинности для предпосылок каждого
правила:
μА1(
– базовые пространства входных
переменных b1и
b2
соответственно) определяются степени
истинности для предпосылок каждого
правила:
μА1( ),
μА1(
),
μА1( ),
μB1(
),
μB1( ),
μB1(
),
μB1( ).
). ),
μA1(
),
μA1( )]
)] ),
μB1(
),
μB1( )]
)] )]
)] )]
)] Y,
а Y
является областью определения, базовым
пространством выходной лингвистической
переменной b3.
Y,
а Y
является областью определения, базовым
пространством выходной лингвистической
переменной b3. ,
где
,
где
 функция
принадлежности ,определенная на
отрезке[0,1]
функция
принадлежности ,определенная на
отрезке[0,1] . Обычное мн-во определяется сов-тью
пар (х,
. Обычное мн-во определяется сов-тью
пар (х, )
) c
функцией принадлежности вида
c
функцией принадлежности вида


 с функцией принадлежности вида
с функцией принадлежности вида

 с функцией принадлежности вида
с функцией принадлежности вида




 ,
ядром
,
ядром
 и модой b.
и модой b.
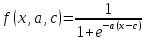
 :
: (первая
строка)
(первая
строка)
 (вторая
строка)
(вторая
строка)
