21. Методы выбора альтернатив в условиях риска( дерево решений)

Дерево решений.

Следующий метод, применяемый для принятия решений в условиях риска, носит название дерева решений. Его применяют тогда, когда необходимо принимать последовательный ряд решений. Дерево решений – графический метод, позволяющий увязать точки принятия решения,возможные стратегии Ai, их последствия Ei,j с возможными факторами, условиями внешней среды. Построение дерева решений начинается с более раннего решения, затем изображаются возможные действия и последствия каждого действия (событие), затем снова принимается решение (выбор направления действия) и т. д., до тех пор, пока все логические последствия результатов не будут исчерпаны.

Дерево решений строится с помощью пяти элементов:

1.Момент принятия решения.

2.Точка возникновения события.

3.Связь между решениями и событиями.

4.Вероятность наступления события (сумма вероятностей в каждой точке должна быть равна 1).

5.Ожидаемое значение (последствия) – количественное выражение каждой альтернативы, расположенное в конце ветви.

Простейшее решение представляет собой выбор из двух вариантов – «Да»

или «Нет» .

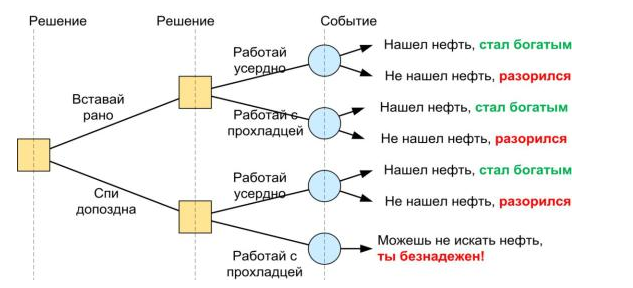
Пример 1. Формула Ж. Поля Гетти «Как стать богатым»:«Вставай

рано»; «Работай усердно»; «Найдешь нефть!».

Моделирование последовательности решений (рис. 21):

1.Решение: Нужно сделать выбор между тем, чтобы «Вставать рано» или

«Спать допоздна» – простейший выбор.

2.Решение: Нужно сделать выбор между тем, чтобы «Работать усердно» или «Спустя рукава» – простейший выбор.

3.Событие: «Найдешь нефть», происходит с определенной вероятностью,

зависящей от последовательности принимаемых решений.

22 Пассивный метод поиска минимума функции одной переменной

Метод оптимизации называется пассивным, когда все точки xi ,i = 1,N, вычислений характеристик задачи (в данном случае значений целевой функции) выбираются одновременно до начала вычислений.

Если N четное, т.е.N = 2l,l = 1,2,", то наилучшее (в смысле максимального уменьшения длины отрезка локализации)

размещение точек xi ,

i =

1, N

, получается разбиением их на рав-

ноотстоящие ε-пары,т.е.

x

2 j −1

= a +

b − a

j − ε ,

x

2 j

= a +

b − a

j + ε ,j = 1,N 2,

(4.1)

N 2+1

N 2+1

2

2

где ε − некоторое малое положительное число.

При этом

b − a

ε

L0

+ ε .

LN=

+

=

N 2+1

2

l +1

2

Если N нечетное,

т.е. N = 2l +1,l = 1,2,", то наилучшим

является равномерное распределение точек, т.е.

x

= a +

b − a

i,

i =

.

(4.2)

1, N

I

N +1

При этом

b − a

L0

LN

= 2

=

.

N +1

l +1

Нетрудно заметить, что использование нечетного числа точек при пассивном методе поиска неэффективно.

	После определения точек					xi , i=	1, N	, вычисляются значе-
ния	функции f (xi ) . Пусть			f (xk )= min f (xi ).						Тогда, полагая
					i =1, N
x0 = a, xN +1 = b,			Определяется			итоговый			отрезок локализации
∆N	= [xk −1,xk +1] .	Точка xk		принимается				за		аппроксимацию

(оценку) точки минимума x , значение функцииf (xk )− за оценку f * = f (x*) , т.е.x*= xk , f*= f(xk ).

Пример. Определить с помощью пассивного поиска ми-

нимум функции

f (x) = x+ 1 ,

заданной на отрезке ∆ = [0,2]: а)

X

при N=6,ε=0,1; б) приN=7.

Решение.

а) N=6,ε

=0,1.

x2j−1,

x2j

Определяем пары точек

с помощью соотноше-

ния (4.1):

2 − 0

j − 0.1 = 0,5j − 0,05,

x2j−1

= 0 +

j =

1,3;

3 +1

2

x2j

= 0 +

2 − 0

j +

0.1 =

0,5 j + 0,05,

j =

1,3.

3 +1

2

Результаты вычислений x и

f (x) заносим в табл. 4.1.

Таблица 4.1

Номер

1

2

3

4

5

6

отсчета

x

0,45

0,55

0,95

1,05

1,45

1,55

f (x)

2,67

2,37

2,0026

2,0024

2,14

2,20

Поскольку

f (x4 )= min f (xi ) ,

то

полагаем

∆6=[x3,x5]=

i =1,6

=[0,95; 1,45], x x4

= 1,05,

f *

f (x4 )= 2,0024.

Ответ: ∆6

= [0,95; 1,45] ,

x* 1,05,

f * 2,0024.