
- •1.Сис анализ в совр исследований
- •2. Сис описание задачи оптимизации
- •3.Сис анализ транспортных моделей. М. Потенциалов
- •4. Алгоритм решения транспортной задачи при получении максзначц.Ф
- •5. Решение транспортных задач методом Фогеля
- •6. Оптимизация назначений максимальное и минимальное значение функции
- •7. Динамическое программирование принцип оптимальности Беллмана
- •8. Постановка задачи распределения инвестиций и алгоритм ее решения методом динамического программирования
- •9. Постановка задачи о бинарном рюкзаке и алгоритм ее решения методом динамического программирования.
- •10. Постановка задачи о рюкзаке с неограниченным количеством элементов и алгоритм ее решения методом динамического программирования.
- •11. Постановка задачи о замене оборудования и алгоритм ее решения методом динамического программирования.
- •12. Принятие решений на основе расчета функции полезности.
- •13. Экспертные методы в процессе прогнозирования и разработки управленческих решений.
- •14. Метод ранжирования мнений экспертов.
- •15.Методы определения согласованности и экспертов
- •16. Метод Паттерн
- •17Методы групповой экспертной оценки:
- •18.Метод "Дельфи"
- •19.Принятие решении в условиях неопределенности
- •20. Охарактеризуйте критериев пессимизма - оптимизма(гурвица) и критериев минимального риска (севиджа).
- •21. Методы выбора альтернатив в условиях риска( дерево решений)
- •22 Пассивный метод поиска минимума функции одной переменной
- •23 Метод дихотомии(половинного деления) как метод оптимизации унимодальной функции
- •24 Численный метод оптимизации функции одной переменной -метод Фибоначчи
- •25. Численный метод оптимизации функции одной переменной – метод «золотого сечения»
- •26. Градиентный метод оптимизации – метод с дроблением шага
- •27.Градиентный метод оптимизации – метод наискорейшего спуска.
- •28. Градиентный метод оптимизации – метод Ньютона
- •29.Понятие нечеткого множества и операции над ними.
- •30.Функции принадлежности элементов нечеткого множества их назначение и виды
- •31 Нечеткие отношения. Понятия и принципы композиции нечетких отношений
- •32Понятие лингвистической переменной. Метод Мамдани
- •32 Метод оптимизации – метод штрафных функций
- •33 Модель черного ящика
- •34 Структуризация конечной цели в виде дерева целей
- •35 Проектирование систем с исследованием системных принципов
- •36 Выбор рациональной стратегии с использованием многих критериев
- •37 Метод функционально стоимостного анализа
- •38 Современные тенденции в области системного анализа
20. Охарактеризуйте критериев пессимизма - оптимизма(гурвица) и критериев минимального риска (севиджа).
Критерий Гурвица – критерий обобщенного максимума, или пессимизма-оптимизма.Представляется логичным, что при выборе решения вместо двух крайностей в оценке ситуации придерживаться некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего, благоприятного поведения природы.
Согласно
этому подходу для каждого решения
необходимо определить линейную комбинацию
min и max выигрыша и взять ту стратегию,
для которой эта величина окажется
наибольшей.Этот критерий
обеспечивает промежуточное решение
Аi между
крайним оптимизмом и крайним пессимизмом,
которое определяется по принципу:
Число (a=1-y)- степень оптимизма, удовлетворяет условию 0≤ a≤ 1 и выбирается из субъективных соображений, особенностей среды, здравого смысла, исходя из опыта ЛПР, его отношения к риску и т.п. На выбор значения степени оптимизма оказывает влияние мера ответственности: чем серьезнее последствия ошибочных решений, тем больше желание принимающего решение застраховаться, то есть степень оптимизма ближе к нулю.
Для каждой строки рассчитывается среднее взвешенное (с учетом выбранного значенияy) наименьшего и наибольшего результатов, после чего выбирается строка с максимальным значением.
Приy=0 имеем критерий крайнего оптимизма, т.е. отражает позицию азартного игрока, ожидающего наиболее благоприятное состояние среды.
Приy=1 критерий Гурвица превращается в критерий крайнего пессимизма Вальда.
Если 0<y<1, то имеем промежуточное отношение ЛПР к возможным рискам. При желании подстраховаться в данной ситуацииy принимают близким к единице.
Выбор значенияy субъективен, а, следовательно, субъективен и выбор решения, что совершенно неизбежно в условиях неопределенности.
Чем опаснее ситуация, тем больше ЛПР стремится застраховать себя от возможных рисков, тем ближеy к 0. А чем менее он азартен, тем y ближе к 1.
Оптимальная по Гурвицу стратегия должна гарантировать статистику больший выигрыш по сравнению с выигрышем, принимаемым статистиком интуитивно или исходя из опыта.
Применение критерия Гурвица оправданно, если ситуация, в которой принимается решение, характеризуется признаками:
-
вероятности состояний природы неизвестны;
-
необходимо считаться с наихудшим из возможных вариантов;
-
решение реализуется малое количество решений;
-
допускается некоторый риск.
Пример:Для
применения критерия Гурвица нужно
знать значение вероятностиy .
Пусть, например,y=0,9 .
Это означает, что событие «наименьший
возможный выигрыш статистикаA »
желаем сделать более правдоподобным
(y близко
к единице), то есть страхуемся от
неблагоприятных ситуаций в игре.
Тогда Запишем
все промежуточные результаты в таблицу.
Запишем
все промежуточные результаты в таблицу.
Из последнего столбца таблицы видно, что максимальное значениеhi равно (–7,2) и соответствует чистой стратегииA3 ; она и будет оптимальной по критерию Гурвица.
Анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет глубже исследовать суть явления и выбрать наиболее обоснованное управленческое решение. В качестве оптимальной на основании совокупных исследований берется та стратегия, которая чаще других называлась оптимальной по всем критериям.
Критерий Сэвиджа (минимаксного риска) – это критерий минимаксного риска, минимизации «сожалений». Этот критерий, как критерий Вальда, является максимально осторожным и пессимистическим.На практике, выбирая одно из возможных решений, часто останавливаются на том, осуществление которого приведет к наименее тяжелым последствиям, если выбор окажется ошибочным.
По принципу Сэвиджа каждое решение характеризуется величиной дополнительных потерь, которые возникают при реализации этого решения, по сравнению с реализацией решения, правильного при данном состоянии природы. Он особенно удобен для экономических задач и часто применяется для выбора решений в играх человека с природой. Естественно, что правильное решение не влечет за собой никаких дополнительных потерь, и их величина равна нулю.
При выборе решения, наилучшим образом соответствующего различным состояниям природы, следует принимать во внимание только эти дополнительные потери, которые по существу, будут являться следствием ошибок выбора.
Для решения задачи строится так называемая «матрица рисков», элементы которой показывают, какой убыток понесет игрок (ЛПР) в результате выбора неоптимального варианта решения.
Риском игрокаrij при выборе стратегии в условиях (состояниях) природы Пjназывается разность между максимальным выигрышем, который можно получить в этих условиях, и выигрышем, который получит игрок в тех же условиях, применяя стратегию.
В критерии Сэвиджа пессимизм проявляется по-другому: худшим считается не минимальный выигрыш, а максимальная потеря выигрыша по сравнению с тем, что можно было бы достичь в данных условиях (максимальный риск).
Критерий Сэвиджа ориентируется не на результат, а на риск (потери или штрафы)rij .
В
качестве оптимальной выбирается
стратегия, при которой величина потерь
в наихудших условиях минимальна. Критерий
Сэвиджа рекомендует выбирать в
качестве оптимальной ту стратегию,
которая минимизирует максимальный
риск:![]() Требования,
предъявляемые к ситуации, в которой
принимается решение по критерию Сэвиджа,
совпадают с требованием к использованию
критерия Вальда. Критерий Сэвиджа, как
и критерий Вальда, ориентирует статистика
на самые неблагоприятные состояния
природы.
Требования,
предъявляемые к ситуации, в которой
принимается решение по критерию Сэвиджа,
совпадают с требованием к использованию
критерия Вальда. Критерий Сэвиджа, как
и критерий Вальда, ориентирует статистика
на самые неблагоприятные состояния
природы.
Пример. Для задачи «Поставщик» мини/макс риска достигается сразу при двух стратегиях А2 и А3:
 Найти
оптимальное решение игры
Найти
оптимальное решение игры  ,
применяя критерий Сэвиджа.
,
применяя критерий Сэвиджа.
Решение.Ориентируемся на самые неблагоприятные состояния «природы». Вычислим риски статистика А.Для первого столбца:

Для
второго столбца:
Для
третьего столбца: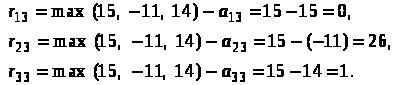
Запишем матрицу
рисков
Определим в каждой строке наибольшее число – наибольший риск статистикаA , если он применяет стратегиюAi , а природа меняет свои состояния П1, П2 , . Дополним матрицу рисков последним столбцом «наибольшие риски».

Найдем
наименьший риск: ![]() .
.
Значит,
оптимальной стратегией по критерию
Сэвиджа является стратегия ![]() .
.
