29.Понятие нечеткого множества и операции над ними.

Нечетким мн-м С в Х наз-ся сов-ть пар вида (x,, где функция принадлежности ,определенная на отрезке[0,1]

Справедливо утверждение: «нечеткое множество вполне описывается своей функцией принадлежности». Обычные(четкие) мн-ва составляют подкласс нечетких мн-в. Для обычного мн-ва функция принадлежности . Обычное мн-во определяется сов-тью пар (х,)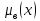

Операции над нечеткими множествами:

1.Объединением нечетких множеств А и В в Х называется нечеткое мн-во А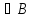 c функцией принадлежности вида

2.пересечением нечетких мн-в А и В в Х называется нечеткое мн-во с функцией принадлежности вида

3. дополнением нечеткого мн-ва А в Х называется нечеткое мн-во с функцией принадлежности вида

4.Разность нечетких мн-в А и В в Х определяется как нечеткое мн-во А-В с функцией принадлежности вида

Декартово произведение А1*А2*….*Аn нечетких мн-в А1 в Х1 определяется как нечеткое мн-во А в декартовом произведении Х=Х1*Х2*….*Хn с функцией принадлежности вида

30.Функции принадлежности элементов нечеткого множества их назначение и виды

1-Треугольная функция

где a,b,c - некоторые числовые параметры, упорядоченные отношением a≤b≤cи принимающие произвольные действительные значения. Функция принадлежности порождает нормальное выпуклое унимодальное нечеткое множество с носителем (a,c), границами (a,c)/, ядром и модой b.

2- Функция принадлежности Гаусса

3- Сигмовидная функция

В зависимости от знака параметра a рассматриваемая ФП будет открыта или справа или слева, что позволит применять её при описании таких нечетких понятий, как «очень большой», «крайне отрицательно» и др.

31 Нечеткие отношения. Понятия и принципы композиции нечетких отношений

Нечеткие отношения

Если элемент u под номером i находится в отношении R с элементом vс номерjм j, то записывают r_ij(u_i,v_j). Отношения можно представить в виде матрицы.

Ui/Vj	1	2	3	4
1	r11	r12	r13	r14
2	r21	r22	r23	r24
3	r31	r32	r33	r34
4	r41	r42	r43	r44

Таблицу можно расписать иначе, в виде «суммы», где знак «+» будет означать лишь факт принадлежности элемента к подмножеству :

(первая строка) (вторая строка)

Композиция отношений

В логике нечетких отношений произведение нечетких множеств моделирует знание-правило «если U, то V», т.е. моделирует отношение-продукцию U→V.

R = U * Vвыполняет операцию U→V,S = V * W₁

Композиция множеств позволяет дать ответ на вопрос: «Как определить отношение вида?»

U * V→V * W₁

В левой части имеем:r_ij = μ_R(u_i,v_j) В правой части имеем:s_ij = μ_S(v_i,ϕ_j)

Сущность операции свертки представляет собой классический алгоритм произведения матриц

R→S

P = R ° S

P₁₁=max

P₃₂=max

32Понятие лингвистической переменной. Метод Мамдани

При формировании базы нечетких правил используются лингвистические переменные, с помощью которых может быть построена система правил след.типа:

ЕСЛИ b₁это А₁ Иb₂ это А₂ ТО b₃ это А₃ или ЕСЛИ b₁это А₁ ИЛИb₂ это А₂ ТО b₃ это А₃

Где b_i – лингвистические переменные;A_j – нечеткие множества, соответствующие базовым или модифицированным с помощью процедур G значениям лингвистической переменной.

В данной записи переменные b₁иb₂ относящиеся к условиям правил, называются входными переменными, а b₃из заключения – выходной лингвистической переменной.

Алгоритм нечеткого вывода по Мамдани.

ЕСЛИ b₁это А₁ Иb₂ это А₂ ТО b₃ это А₃ ЕСЛИ b₁это В₁ Иb₂ это В₂ ТО b₃ это В₃

Этап 1. Фазификация входных переменных: по фактическим точным значениям входных переменных ,( где – базовые пространства входных переменных b₁и b₂ соответственно) определяются степени истинности для предпосылок каждого правила: μ_А1(), μ_А1(), μ_B1(), μ_B1().

Этап2. Нечеткий вывод состоит из двух действий – агрегирования предпосылок и активизации заключений правил. Сначала находятся степени истинности правил, в данном случае с использованием операции min, т.к. употребляются логические связки «И»:

a₁=min[μ_A1(), μ_A1()]

a₂=min[μ_B1(), μ_B1()]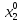

Затем определяются «усеченные» функции принадлежности для заключений правил:

μ’_A1(y)=min[a₁,μ_A1()]

μ’_B1(y)=min[a₂,μ_B1()]

где yY, а Y является областью определения, базовым пространством выходной лингвистической переменной b3.

Этап 3. Аккумуляция заключений нечетких правил. Найденные «усеченные» функции объединяются, в результате чего получается итоговое нечеткое множество для входной переменной с функцией принадлежности:

μ(y)=max[μ’_A1(y), μ’_B1(y)]

Этап 4. Дефазификация для нахождения, если это требуется, точного y0.