Министерство образования республики Беларусь

Белорусский национальный технический

университет

Кафедра физики

Методические указания к лабораторной работе № 23

Определение модулей кручения и сдвига методом крутильных колебаний

для студентов строительных специальностей

Минск 2006

УДК 531.38(076.5)

ББК 22.213.я7

062

В работе изложен экспериментальный метод определения модуля кручения и модуля сдвига упругого материала в виде струны методом крутильных колебаний. Рассмотрены оценки модуля Юнга и модуля всестороннего сжатия исследуемого материала.

Составители: А.А. Баранов, А.П. Каравай

Рецензенты: И.А. Сатиков, В.Н. Кудин

© Белорусский национальный технический университет, 2006

Цель работы: 1. Определить методом крутильных колебаний модули кручения и сдвига струны.

2. Получить оценки численных значений модуля Юнга и модуля всестороннего сжатия материала струны.

1. Упругие свойства твердых тел.

В теории упругости изучают действия только статических нагрузок на твердые тела. Динамические нагрузки представляют собой волны в телах.

Под влиянием внешних статических силовых (не температурных) воздействий тела испытывают деформацию, т.е. меняют форму и размеры. В линейной теории упругости изучают только малые напряжения (нагрузки).

Рассмотрим следующие виды деформаций: сжатие (растяжение), сдвиг, всестороннее сжатие, кручение.

а) Для продольных упругих деформаций изотропных твердых тел (стержней, струн) справедлив закон Гука: относительная деформация  пропорциональна напряжению :

, (1)

где – напряжение, т.е. внешняя сила F отнесенная к единице площади поперечного сечения тела (стержня), – относительная деформация тела, т.е. отношение абсолютной деформации к начальной длине тела (стержня) , l – длина после нагрузки; Е – модуль продольной упругости или модуль Юнга.

Модуль Юнга  – числено равен напряжению при относительной деформации равной единице.

б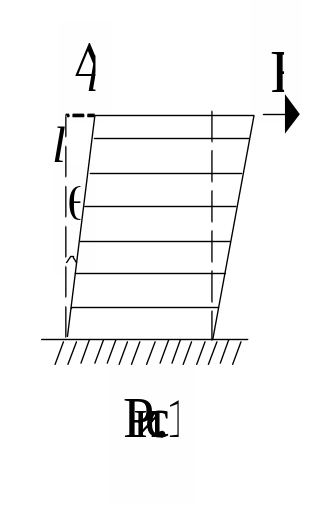 ) Сдвиг – деформация, при которой все плоские слои твердого тела, параллельные некоторой закрепленной плоскости (плоскости сдвига) смещаются параллельно друг другу не искривляясь и не изменяясь в размерах. Сдвиг происходит под действием силы F, приложенной к грани параллельной плоскости сдвига (рис.1).

Мерой деформации является угол сдвига , измеряемый в радианах.

По закону Гука: относительный сдвиг  пропорционален касательному (скалывающему) напряжению , т.е.

. (2)

Здесь модуль сдвига численно равен касательному напряжению, вызывающему относительный сдвиг, равный единице.

Относительное продольное растяжение (сжатие) тела сопровождается его относительным сужением (расширением) , где d – поперечный размер тела.

Коэффициентом Пуассона (модулем поперечного сжатия)  называется отношение относительного поперечного сужения (расширения) к относительному продольному удлинению (сжатию) , т.е.

. (3)

Из теоретических соображений [1,7] коэффициент Пуассона  заключен в пределах

–1    0,5.

Материалы с отрицательным  неизвестны. Для большинства твердых тел из опыта   0,25.

в) Деформация всестороннего сжатия (растяжения) – уменьшение (увеличение) объема тела без изменения его формы под влиянием равномерно распределенных по всей поверхности тела сжимающих (растягивающих) сил.

По закону Гука имеем:

, (4)

где – относительное изменение объема тела под действием напряжения .

Здесь модуль всестороннего сжатия (объемной упругости) численно равен напряжению при относительном изменении объема равном единице.

Из теории упругости [1,7] вытекают следующие связи модулей G, E, K [1,7]

(5)

(6)

г) Кручением называются деформация тела (струны) с одним закрепленным концом под действием пары сил, плоскость которой перпендикулярна к оси тела. Момент М этой пары сил называется крутящим (вращательным) моментом.

Для цилиндрической формы (струны, стержня) по закону Гука угол закручивания  отнесенный к длине струны L, т.е. относительная деформация пропорциональна крутящему моменту М, т.е.

(7)

Модуль кручения численно равен вращательному моменту при относительном угле закручивания равном единице.

Для анизотропных твердых тел напряжения и деформации являются тензорами второго ранга [4].

В декартовых координатах тензор напряжений равен

,

тензор деформаций .

Эти тензоры линейно связаны между собой.

Для анизотропных кристаллов закон Гука принимает вид

,

где i, j, k, l = 1, 2, 3 и по повторяющимся индексам предполагается суммирование. Число модулей упругости тензора сводятся к 21 в виду симметрии тензора и [4]. В самом простейшем изотропном случае получается только два модуля Е и G.