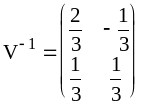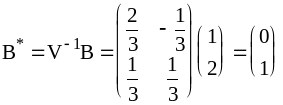Лекция 17
Тема: Системы оптимального управления
План лекции:
Основные понятия.
Управляемость динамических систем.
Наблюдаемость.
Принцип максимума Л.С.Понтрягина.
1. Системы оптимального управления
Системой оптимального управления называется система, качество функционирования которой удовлетворяет какому-либо критерию оптимальности. Наиболее часто используются
следующие критерии :
1) критерий максимального быстродействия;
2) среднеквадратичный критерий.
Система называется оптимальной по быстродействию, если
время переходного процесса минимально возможное.
Система оптимальна по критерию (2), если минимизируется :
а) энергия управления;
б) отклонение траектории движения системы от заданной.
Основными понятиями теории оптимального управления
являются такие, как :
- переменные состояния;
- пространство состояний;
- критерий оптимальности;
- ограничения;
- управляемость;
- наблюдаемость и т.д.
Для решения задач оптимального управления обычно используются модели пространства состояний.
2. Управляемость динамических систем
Система называется полностью управляемой, если она
может
быть переведена из любого исходного
состояния
![]()
в
момент времени
![]() в
другое состояние
в
другое состояние
![]() в
момент времени
в
момент времени
![]()
за
конечное время
![]() при кусочно - непрерывном управляющем
воздействии.
при кусочно - непрерывном управляющем
воздействии.
Система называется неполностью или частично
управляемой, если часть переменных состояния не управляемы.
Существуют методы анализа управляемости динамических систем.
Наиболее часто используется метод, основанный на
анализе управляемости с использованием канонической модели пространства состояний.
Если
задан вектор состояния
![]() ,
который может быть задан неоднозначно,
то от него можно перейти к вектору
состояния
,
используя матрицу линейного преобразования
,
который может быть задан неоднозначно,
то от него можно перейти к вектору
состояния
,
используя матрицу линейного преобразования
![]() .
.
Переход
осуществляется следующим образом :
![]() .
.
Пусть имеется исходная модель пространства состояний :
Переход
: 1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
![]() ,
,
![]() ,
,
где
![]() ,
,
![]()
Модель пространства состояний называется канонической,
если матрица состоит из собственных векторов системы :
![]() ,
,
![]() .
.
Анализ управляемости состоит в следующем :
1) Переход от исходной модели пространства состояний
к
канонической форме. Для этого необходимо
вычислить
![]() собственных векторов системы :
собственных векторов системы :
.
2)
Анализ матриц
![]() и
и
![]() канонической модели.
канонической модели.
Существует несколько алгоритмов вычисления собственных векторов системы. Рассмотрим 2 метода :
1)прямой, который можно использовать для любой модели пространства состояний;
2)
метод для коагулированной матрицы
состояний
![]() .
.
Прямой метод
Пусть имеется автономная система (управляющее
воздействие равно нулю) :
(1)
![]() .
.
Решением данного уравнения является следующая система уравнений :

где
![]() переменные
состояния.
переменные
состояния.
![]()
![]()
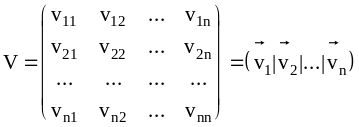
![]()
![]() (2)
(2)
![]() собственные
вектора системы.
собственные
вектора системы.
![]() матрица
собственных векторов системы.
матрица
собственных векторов системы.
![]() собственные
числа матрицы
,
то есть корни
собственные
числа матрицы
,
то есть корни
следующего уравнения :
![]() ,
где
,
где
![]() единичная
матрица,
единичная
матрица,
Продифференцируем уравнение (2) по времени :
![]() .
.
Подставим правую часть уравнения (2) в уравнение (1) :
![]() .
.
Приравняем правые части полученных уравнений :
![]() (3)
(3)
![]() (4)
(4)
При вычислении собственных векторов один из элементов векторов обычно задается равным 1, например, первый элемент.
Пример.
Пусть
![]() .
.
Найти
собственные вектора системы
![]() .
.
1) Найдем собственные числа :
![]()
![]()
![]()
![]()
![]()
![]()
2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Алгоритм Вандермонда
Алгоритм Вандермонда применяется для моделей пространства состояний, заданных в коагулированной форме.


После
нахождения
![]() модель пространства состояний
модель пространства состояний
имеет
вид :
![]() ,
,
где
![]() диагональная матрица,
диагональная матрица,
![]() .
.
Такая
форма модели пространства состояний
называется канонической. С ее помощью
можно проверить управляема ли данная
система или нет. Система полностью
управляема, если в матрице
![]() нет ни одной нулевой строки.
нет ни одной нулевой строки.
Пример.
Имеется система вида:
![]()
,
![]()
Проверим
управляемость этой системы и запишем
уравнение системы. Признаком того, что
система является неуправляемой по
![]() ой
переменной состояния является то, что
в дифференциальном уравнении для
ой
переменной
ой
переменной состояния является то, что
в дифференциальном уравнении для
ой
переменной
состояния
нет входного сигнала
![]() .
.
При диагональной канонической форме модели пространства состояний дифференциальные уравнения для каждой переменной состояния не содержат других переменных состояния.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,