Застосування відрізків довгої лінії.

Л

інію без втрат довжиною часто використовують в якості проміжного елементу для узгодження режиму роботи іншої лінії і навантаження не рівного хвильовому опору лінії. При безпосередньому приєднанні лінії з хвильовим опором до навантаження (рис.) з у лінії поряд з бігучою хвилею буде існувати і відбита і лише частина потужності від генератора буде передаватись у навантаження. Для погодження основної лінії з навантаженням між ними вмикають відрізок лінії довжиною з хвилевим опором . Тоді вхідний опір чверть хвилевого відрізка навантаженого на визначається наступною формулою

. І якщо покласти то основна лінія буде узгоджена. Для цього необхідно мати лінію з хвилевим опором з якої і виготовляється відрізок.. У такому випадку відрізок лінії без втрат довжиною називають чверть хвилевим трансформатором , оскільки з його допомогою опір навантаження ніби то перетворюється (трансформується) у опір лінії.

П

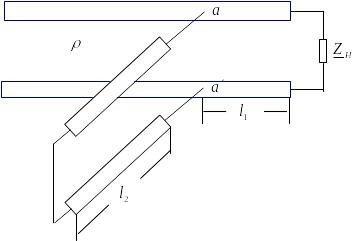
ри комплексному навантаженні знаходять переріз на віддалі від кінця лінії, у якому вхідна провідність . Зверніть увагу на те, що у цьому перерізі активна складова вхідної провідності повинна бути величиною оберненою хвильовому опору лінії. 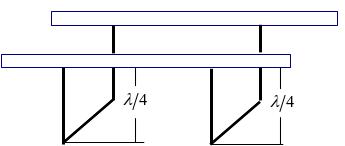До точок підключають короткозамкнений шлейф (шлейф Татарінова) і підбирають його довжину так, щоб його вхідна провідність компенсувала реактивну складову провідності (рис.). Тоді ділянка лінії передачі, що розташована зліва від точок , буде навантажена хвилевим опором і, отже, у лінії буде мати місце режим погодження.

З

начний вхідний опір короткозамкненого відрізка лінії довжиною дає можливість використати його в якості елемента кріплення для двопровідної лінії передачі (рис.). Слід звернути увагу на те, що як чверть хвилевий трансформатор, шлейф Татарінова так і елемент кріплення виконують свої функції лише на певній частоті, на яку вони розраховані (інколи говорять, що це елементи ’’резонансного’’ типу).

Штучні лінії.

С

трогий аналіз електромагнітних процесів у лініях передачі можна здійснити лише за допомогою рівнянь Максвела. Проте у квазістаціонарному наближені елемент довгої лінії без втрат довжиною (рис.) ми замінили на комбінацією поздовжньої індуктивної котушки індуктивністю та поперечного конденсатора ємністю . Потім скористалися законами Кірхгофа, і спрямувавши отримали телеграфні рівняння, розв’язок яких і описує розподіл напруги та струму вздовж довгої лінії.

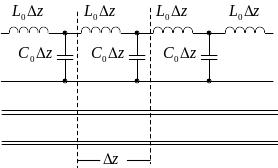
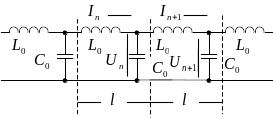
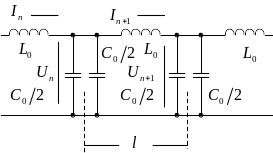
У радіоелектроніці поряд з довгими лініями використовуються штучні лінії побудовані на елементах із зосередженими параметрами, а фізичний розмір таких комірок має скінчену довжину (див. рис.). Для більш детального розгляду процесів у штучній лінії кожну із комірок доцільно подати у вигляді симетричного П-подібного чотириполюсника (рис.)

О

скільки чотириполюсники, що утворюють штучну лінію симетричні і з’єднані каскадно то

та ,

тут - коефіцієнт фази.

З іншої сторони на основі законів Кірхгофа:

,

.

Виключаючи із рівнянь () і () та отримаємо одну із форм дисперсійного рівняння

,

де - .

Г

рафічно дисперсійна залежність показана на рис.

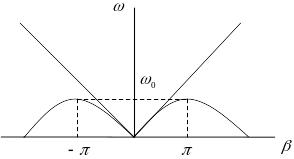
Якщо , то , або . Точно такий набіг фази на довжині може створити хвиля, хвильове число якої задовольняє умові . На рис. такій залежності відповідають прямі лінії. Причому верхній знак відповідає хвилі що поширюється у напрямку зростання координати а нижній знак відповідає хвилі, що поширюється у протилежному напрямку. Отже стандартна форма дисперсійного співвідношення у низькочастотному діапазоні має такий вигляд:

,

де та - індуктивність та ємність штучної ліній на одиницю довжини (погонні параметри). Таким чином штучна лінія виготовлена із конденсаторів ємністю та індуктивних котушок індуктивності у низькочастотному діапазоні поводить себе як довга лінія з погонними параметрами .та . Зокрема фазова швидкість поширення хвиль у такій лінії становить , а хвилевий опір чисто активний і дорівнює . Для порівняння знайдемо фазову швидкість електромагнітних хвиль у коаксіальній лінії передачі з та і у штучній лінії з параметрами : м, Гн, Ф. Для коаксіальної лінії - м/с. Для штучної лінії - м/с. Тому штучну лінію можна використовувати у якості лінії затримки.

У високочастотному діапазоні (при ) фазовий набіг повинен бути комплексним числом, тобто , і дисперсійне рівняння () набуває форми

.

Звідки

.

Розв’язок цих рівнянь дає та . Напруга на виході комірки штучної лінії

.

Множник вказує на те , що при проходженні комірки штучної лінії амплітуда хвилі згасає, інший множник описує фазовий зсув від комірки до комірки. Отже високочастотні хвилі ( ) затухають, а низькочастотні ( ) поширюються без ослаблень.

У високочастотному діапазоні ( ) при та

.

Враховуючи, що ,

.

Тому дисперсійне співвідношення () набуває форми

.

Х

арактерною особливістю дисперсійного відношення () є нелінійна залежність між та . Це означає, що із зміною частоти змінюється і фазова швидкість поширення хвиль, тобто .

У випадку модульованого сигналу кожна із гармонік поширюється із своєю фазовою швидкістю і тому з часом змінюється відстань між гармоніками , що відбивається на зміні параметрів сигналу вздовж лінії передачі. Лінії передачі для яких називаються лініями передачі з дисперсією. Для таких ліній окрім фазової швидкості вводиться поняття групової швидкості. Розглянемо один із традиційних варіантів доведення, де з’являється поняття групової швидкості.

Нехай до початку лінії передачі з дисперсією підводиться амплітудно-модульоване коливання з подавленою несучою, тобто при

.

Якщо спектральна густина модулюючого сигналу дорівнює , тобто , то тоді на основі теореми про модуляцію

.

Оскільки лінія без втрат має наступний коефіцієнт передачі , то спектральна густина сигналу у довільній точці лінії

.

Скористаємося оберненим перетворенням Фур’є для знаходження сигналу

+

.

Для знаходження двох останніх інтегралів у явному вигляді скористаємося наступними припущеннями: - вузькосмуговий сигнал, і, ширина його спектру значно менше від частоти несучого коливання ( ). У першому інтегралі різницю позначимо через , а розкладемо в ряд і обмежимося членами другого і вище порядків малості - . Тоді

, а

У другому інтегралі - частина спектральної густини, що зосереджена у області від’ємних частот поблизу частоти , тому доцільно покласти . Тоді , ,

а =

.

Отже

=

= .

Як видно із () несуче коливання поширюється із фазовою швидкістю , а обвідна низькочастотного сигналу зберігає свою форму , проте з’являється у точці із деяким запізненням , причому , тобто запізнення зумовлене швидкістю яка і називається груповою швидкістю. Отже

.