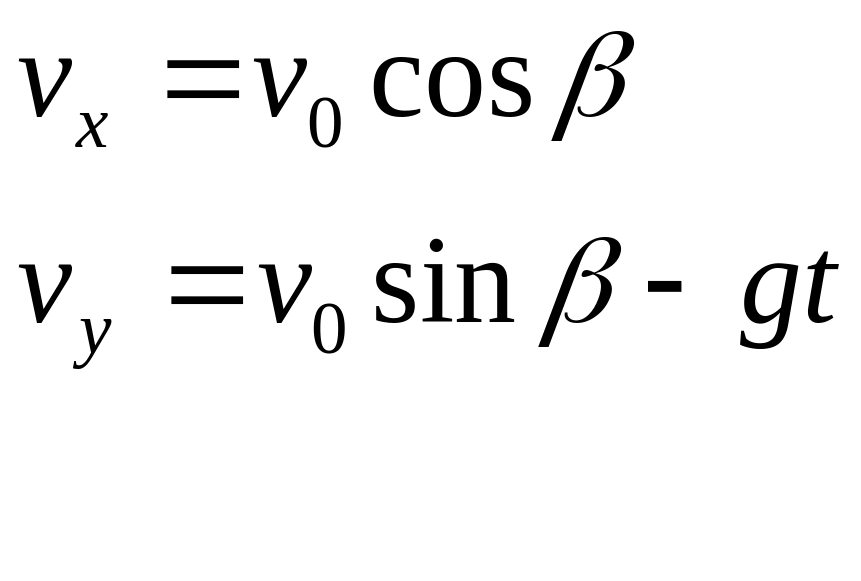Кінематика.
Основні формули.
Радіус-вектор
![]() точки
1 – це вектор, проведений в цю точку з
початку відліку, його проекції на осі
прямокутної системи координат
(Мал.1):
точки
1 – це вектор, проведений в цю точку з
початку відліку, його проекції на осі
прямокутної системи координат
(Мал.1):
|
де
![]() - координати точки.
- координати точки.
Вектор
переміщення
з точки 1 у точку 2: ![]() ,
,
де
![]() -
радіус-вектори точок 1 і 2.
-
радіус-вектори точок 1 і 2.
Вектор
середньої швидкості переміщення
за час
![]() :
:
![]()
Вектор
миттєвої швидкості
![]() :
:
![]()
Середня
шляхова швидкість:
![]() ,де
,де
![]() =
=![]() - шлях, пройдений тілом з точки 1 до точки
2.
- шлях, пройдений тілом з точки 1 до точки
2.
Вектор
середнього прискорення:![]()
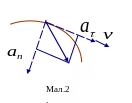
Вектор прискорення (Мал.2.):
![]()
Прискорення точки в проекціях на дотичну і нормаль траекторії:
![]() -
тангенціальне прискорення,
-
тангенціальне прискорення,
![]() - нормальне
прискорення,
- нормальне
прискорення,
де
![]() - радіус кривизни траєкторії.
- радіус кривизни траєкторії.
Рівноприскорений
рух:
![]() ,
,
![]() ,
,
![]()
де
![]() - радіус-вектор початкового положення
тіла,
- радіус-вектор початкового положення
тіла,
![]() - його початкова швидкість.
- його початкова швидкість.
Р
Радіус-вектор
тіла:
ОХ:
ОУ:
|
Найбільша
висота підйому
![]() ,
дальність польоту
,
дальність польоту
![]() .
.
|
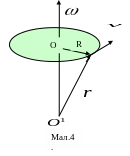
В ектор
кутової швидкості:
ектор
кутової швидкості:
![]()
Вектор
кутового прискорення:
![]()
Зв’язок
між лінійними і кутовими величинами:
![]() ,
,
![]() ,
,
![]()
-
радіус-вектор відносно довільної точки
на осі обертання,
![]() - відстань до осі обертанн
я.
- відстань до осі обертанн
я.
середня
кутова швидкість:
![]() (
рад/с);
(
рад/с);
середнє
кутове прискоренн
![]() (рад/с2).
(рад/с2).
Рівномірний
рух по колу:
![]() (рад)
– кутова координата;
(рад)
– кутова координата;
![]() (с)
- період
- час одного оберту;
(с)
- період
- час одного оберту;
|
|
Приклади розв’язування задач.
Задача
1.
Рівняння прямолінійного руху тіла
вздовж осі ОХ має вигляд:
![]() .
Знайти швидкість тіла в момент часу
.
Знайти швидкість тіла в момент часу
![]() .
В який момент часу після початку руху
тіло змінить напрямок руху на протилежний?
В який момент тіло повернеться в точку
з координатою
.
В який момент часу після початку руху
тіло змінить напрямок руху на протилежний?
В який момент тіло повернеться в точку
з координатою
![]() ?
?
Дано:
1)
![]() =?
, 2)
=?
, 2)
![]() =?,
3)
=?,
3)
![]() =0,
=0,
![]() =?
=?
Розв’язок.
Знайдемо
швидкість і прискорення тіла:
![]() 12-8
12-8![]() (м/с) (1)
(м/с) (1)
![]() (м/с2)
(2)
(м/с2)
(2)
В момент
часу
швидкість
![]() (м/с).
(м/с).
Тіло
змінює напрям руху на протилежний в
момент зупинки (
=0),
отже час![]() зміни
напрямку руху знайдемо з рівняння: 12-8
=0
і
отримаєм
=1,5
(с) (3)
зміни
напрямку руху знайдемо з рівняння: 12-8
=0
і
отримаєм
=1,5
(с) (3)
Знайдемо час зумови задачі ,
якщо =0, то 5+12 -4 2=0,
Запишемо це рівняння в канонічному вигляді: 4 2-12 -5=0, (4)
звідки, розв’язавши його, отримаємо: =3,375 с.
Відповідь: = - 12м/с; =1,5с; = 3,375с.
Задача 2. Один із способів оцінки якості автомобіля ґрунтується на визначенні того, наскільки швидко він розганяється до швидкості 60км/годину. У деяких автомобілів прискорення обмежується не потужністю двигуна, а проковзуванням коліс. Хороші шини забезпечують прискорення приблизно 0,5 . Скільки часу і який шлях потрібний для розгону автомобіля до швидкості 60км/годину?
Дано: =0
![]()
=60км/годину = 16,8 м/c
=?, =?
Розв’язок.
Так як початкова швидкість =0 і рух рівноприскорений, то:
![]() , (1)
, (1)
звідки
час розгону
![]() с
с
Шлях,
пройдений за час розгону:
![]() м.
м.
По
аналогії з цим прикладом можна визначити
мінімальний час і гальмівний шлях до
повної зупинки автомобіля, якщо його
мінімальне прискорення
![]() м/с2,
а початкова швидкість
м/с2,
а початкова швидкість
![]() м/с2:
м/с2:
![]() , (2)
в
момент зупинки
=0,
отже час до зупинки:
, (2)
в
момент зупинки
=0,
отже час до зупинки:
![]() с.
с.
Як і можна було сподіватися, ми отримали такий самий час, як і при розгоні. Отже гальмівний шлях буде дорівнювати 28,3м.
Відповідь: = 3,4с; = 28.3м.
З адача
3
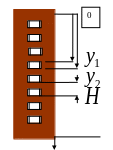
.Людина знаходиться в кімнаті на п’ятому
поверсі і бачить, як мимо його вікна
пролітає зверху квітковий горщик.
Відстань 2м, що дорівнює висоті вікна,
горщик пролетів за 0,1 с. Висота одного
поверху 4м. Вважаючи
=10
м/с2,
визначте, з якого поверху впав горщик.
адача
3
.Людина знаходиться в кімнаті на п’ятому
поверсі і бачить, як мимо його вікна
пролітає зверху квітковий горщик.
Відстань 2м, що дорівнює висоті вікна,
горщик пролетів за 0,1 с. Висота одного
поверху 4м. Вважаючи
=10
м/с2,
визначте, з якого поверху впав горщик.
Дано:
![]() =2
м
=2
м
![]() =0.1
с
=0.1
с
![]() =4
м.
=4
м.
![]() =?
=?
Розв’язок.
Рух
горщика рівноприскорений (опором повітря
нехтуємо), його початкова швидкість
=0.
Початок координат виберемо в точці
початку руху вісь ОУ спрямуємо з). вниз.
Координата верхньої і нижньої частин
рами вікна
![]() і
і
![]() ,
причому
,
причому
![]() .
Отже:
.
Отже:![]() (1)
(1)
![]()
![]() (2)
(2)
Враховуючи,
що
![]() ,
а
,
отримаємо:
,
а
,
отримаємо:
![]() (3)
(3)
Знайдемо час падіння тіла до верхньої частини вікна з виразу (3):
![]() =
=![]()
![]() .(4)
.(4)
Координата верхньої частини вікна:
![]() м. (5)
м. (5)
Висота
одного поверху
![]() 4м,
тому горщик пролетів
4м,
тому горщик пролетів
![]() поверхів, а падав горщик з
поверхів, а падав горщик з
![]() 25
поверху.
25
поверху.
Відповідь: = 25.
Задача 4. З підводного човна запускається балістична ракета, наведена на місто, яке знаходиться на відстані 3000км від човна. За який час ракета долетить до цілі і яка її стартова швидкість ? При цьому будемо вважати Землю плоскою, прискорення вільного падіння сталим ( =9.8 м/с2 ), опором повітря і води нехтуємо.
Дано:
![]() =
3*106м/с
=
3*106м/с
=?, =?
Розв’язок.
Спочатку вияснимо, під яким кутом треба запустити ракету, щоб вона досягла точки на поверхні Землі. Рух ракети рівноприскорений, тому рівнянням руху є:
1 ![]() (1)
(1)
|
ОХ:
![]()
ОУ:
![]()
Швидкість ракети змінюється за формулою:
![]()
В проекціях на осі ОХ і ОУ:
ОХ:
![]()
ОУ:
![]()
Траєкторія
ракети – парабола. В найвищій точці
траєкторії вектор швидкості паралельний
осі ОХ, отже
![]() і
і
![]() .
Звідси отримаємо час підйому ракети :
.
Звідси отримаємо час підйому ракети :
![]() .
(2)
.
(2)
Час руху
ракети від запуску до цілі:
![]() .
(3)
.
(3)
Підставимо в формулу для координати і отримаємо дальність польоту:
![]() (4)
(4)
Максимальна
дальність польоту буде досягнута, якщо
ракету націлити під кутом
![]() =450.
=450.
Знайдемо початкову швидкість ракети:
![]() =
=![]() км/с.
км/с.
Повний час руху ракети буде:
![]() хв.
хв.
З цього прикладу видно, що в випадку ракетного нападу максимальний запас часу становить приблизно 10 хвилин, що замало для евакуації міста.
Вияснимо,
на яку найбільшу висоту піднімається
ракета. Для цього підставимо час
в формулу для
![]() :
:
![]() м=749 км
м=749 км
Відповідь: = 5,42км/с, = 13хв.
Задача
5.
Тіло рухається по колу так, що його
кутова координата змінюється з часом
за формулою:![]() ,
де
,
де
![]() =3
рад/с. а
=3
рад/с. а
![]() =
5 рад/с3.
Знайти:
=
5 рад/с3.
Знайти:
а) залежність кутової швидкості і кутового прискорення від часу; б) час до зупинки;
в) кутове прискорення в момент зупинки.
Дано:
=3 рад/с.
= 5 рад/с3
а)![]() -?,
б)
-?,
б)
![]() -?
в)
-?
в)
![]() -?
-?
Розв’язок.
Модуль кутової швидкості :
![]() (1)
(1)
Модуль
кутового прискорення:
![]() (2)
(2)
В момент
зупинки (
![]() )
кутова швидкість дорівнює нулю, отже:
)
кутова швидкість дорівнює нулю, отже:
![]() (3)
(3)
і з (3)
отримаємо, що:
![]() с.
с.
Кутове прискорення в момент зупинки:
![]() рад/с2.
рад/с2.
Відповідь:![]() ;
= 0,067с;
= -1рад/с2.
;
= 0,067с;
= -1рад/с2.
Задача 6. Знайти кутову швидкість хвилинної стрілки на годиннику. а також лінійну швидкість її кінця, якщо довжина стрілки = 1см.
Дано: = 1см=10-2 м.
=?, =?
Розв’язок
Хвилинна стрілка годинника робить один повний оберт за 1 годину (3600 с).
Кутова швидкість стрілки:
![]() . (1)
. (1)
Лінійна швидкість кінця стрілки : = (2)
Підставимо
числові значення в формули (1) і (2):
=2*3,14:3600=0,0017
рад/с,
![]() 0,0017*0,01=17*10-4
м/с.
0,0017*0,01=17*10-4
м/с.
Відповідь: =0,0017рад/с, =17*10-4м/с
Задача 7. Колесо обертається з кутовим прискоренням 2рад/с2. Через 0,5с після початку руху повне прискорення колеса 0,136м/с2. Знайти радіус колеса.
Дано: = 2рад/с2,
-?
|
|
Розв’язок.
Кутова
швидкість колеса:
![]()
Лінійна
швидкість точки
на
ободі колеса
дорівнює
![]()
Тангенціальне
прискорення:![]() .
Нормальне прискорення:
.
Нормальне прискорення:![]() (4)
(4)
Повне
прискорення точки
знайдемо за теоремою Піфагора:
![]() =
=![]() (5)
(5)
З формули
(5) виразимо радіус колеса
![]()
і в
отриману формулу підставимо числові
значення:
=![]() =
0,062м
=
0,062м
Відповідь: =0,06м.

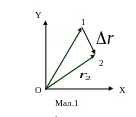
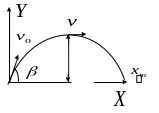
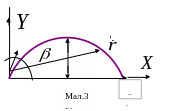 ух
тіла, кинутого під кутом до горизонту
(опором
повітря нехтуємо,
ух
тіла, кинутого під кутом до горизонту
(опором
повітря нехтуємо,