
- •Количественные характеристики надежности, критерии безотказности и восстанавливаемости.
- •Вероятность безотказной работы элемента.
- •В ероятность безотказной работы системы p(t).
- •Ч астота отказов f(t).
- •Интенсивность отказов (t).
- •С вязь - характеристики с другими параметрами надежности.
- •Среднее время безотказной работы
- •С ущность расчета надежности.
- •Экспоненциальный закон надежности.
- •Приближенные расчеты надежности.
- •12. Окончательный расчет надежности.
- •Наработка на отказ т0.
- •14. Эксплуатационные коэффициенты надежности.
- •1 5. Оценка надёжности технических устройств по результатам испытаний.
- •16. Контроль надежности по результатам испытаний.

Количественные характеристики надежности, критерии безотказности и восстанавливаемости.
Качественного определения надежности является недостаточным, т.к. не позволяет, во-первых задать требования надежности к проектируемым системам, во-вторых, сравнивать различные варианты систем, в третьих, рассчитывать необходимый запас по надежности. В связи с этим возникает потребность в ведении количественных характеристик надежности, поскольку отказы и сбои элементов являются случайными событиями, то теория вероятности и математическая статистика являются основным аппаратом, используемым при исследовании надежности, а сами характеристики надежности выбраны из числа показателей принятых в теории вероятности.
Критерий надежности - мера, посредством которой производится количественная оценка надежности. Четыре группы критериев:
Критерии безотказности
вероятность безотказной работы
частота отказов
интенсивность отказов
среднее время безотказной работы
наработка на отказ (среднее время исправной работы между 2 отказами)
Критерии восстанавливаемости
вероятность восстановления
среднее время восстановления
интенсивность восстановления
Критерии технического обслуживания
вероятность обслуживания
среднее время обслуживания
Эксплуатационные коэффициенты надежности
коэффициент использования
коэффициент готовности
коэффициент простоя
коэффициент стоимости обслуживания

Вероятность безотказной работы элемента.
-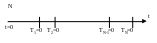 вероятность того, что в заданном интервале
времени t
в элементе не возникнет отказ.
вероятность того, что в заданном интервале
времени t
в элементе не возникнет отказ.
Если взять группу, состоящую из N одинаковых элементов и поставить их на испытания то графически процесс испытания будет выглядеть так:
Так как отказ- случайная величина, то нельзя заранее сказать чему будет равно время работы i элемента, но можно определить вероятность того, что он не откажет в течении заданного времени t. Это может быть определено по данным испытания. Практически для вероятности безотказной работы p(t) используется следующая статистическая оценка p*(t)=[N-n(t)]/N, где N- число элементов на испытании, n(t)- число элементов отказавших в течении времени t. Точность оценки будет тем выше, чем больше N, в пределе статистическая оценка будет стремится к истинному значению при N к бесконечности: p*(t)=Lim[N-n(t)]/Np(t).
В ероятность безотказной работы системы p(t).
Вероятность того, что в заданном интервале времени t в системе не возникнет отказ. Если элементы в системе соединены последовательно относительно надежности, то выход из строя хотя бы одного элемента приводит к отказу всей системы. Если вероятности безотказной работы элементов в системе будут p1(t), p2(t),.. pN(t) то в соответствии с теоремой умножения вероятности (вероятность произведения 2х событий равна произведению вероятности одного из них на условную вероятность другого, при условии что первая имело место) вероятность безотказной работы системы имеет вид: P(t)= p1(t) p2(t)... pN(t). Если p1(t)= p2(t)= pN(t), тогда P(t)=[p(t)]N. Так как вероятность безотказной работы элементов всегда меньше единицы, то из расчетов следует: 1) надежность системы уменьшается при увеличении числа элементов в ней; 2) вероятность безотказной работы системы всегда меньше вероятности безотказной работы самого ненадежного элемента.
ВЕРОЯТНОСТЬ ОТКАЗА СИСТЕМЫ Q(t).
Под вероятностью отказа системы понимают вероятность того, что за малый интервал времени t в системе произойдет отказ, т.е. время исправной работы системы будет меньше заданного. Так как безотказная работа и отказ- события противоположные, то Q(t)=1-P(t)
Q(t)=1-{[1- [1-q2(t)]... [1-qN(t)]} при q(t)- одинаковых Q(t)=1-[1-q(1)]N. Если надежность оценивается для малых промежутков времени, когда вероятность отказа много меньше 1, тогда Q(t)=1-{1-[q1(t)+ q2(t)+... qN(t)]}=qi(t)(от 1 до N). Если вероятность отказов элементов равны, то Q(t)=Nq(t).
