
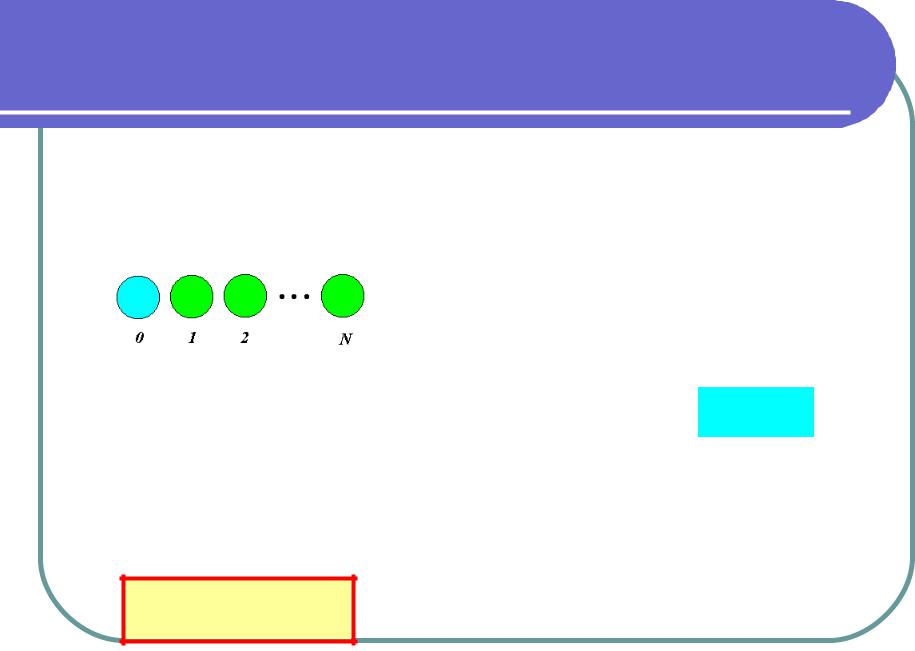
3.2.Поверхностные состояния. Метод ЛКАО
На поверхности |
Энергетический спектр электронов отличается от |
|
имеющегося в бесконечном кристалле |
||
|
Рассмотрим конечную одномерную цепочку, состоящую из N+1 атомов
Необходимо найти волновые функции и собственные значения энергии
H E
Метод ЛКАО |
в виде линейной комбинации |
cm m |
|
|
|
|
атомных орбиталей |
m |
|
|
Rm |
атомная орбиталь, центрированная на атоме m |
||
m r |
||||
|
|
cm - коэффициент, характеризующий удельный вес |
||
m-орбитали.
случай s -атома, т.е. имеющего один электрон на внешней оболочке
|
|
cmH m E cm m |
|
m |
m |

cmH m E cm m
m |
m |
Элементы
Hnn
Hnm при n m.
Snm *n md
Умножим слева на комплексно сопряженную волновую функцию n-атома и проинтегрируем по всему пространству.
Hnm n*H md
Энергия электронного состояния на n-атоме
Была бы равна энергии ионизации свободного атома, если можно было бы пренебречь влиянием его соседей по цепочке
резонансный интеграл
интеграл перекрытия.
характеризует перекрытие атомных волновых функций
Матричные элементы неравнозначны. Атомные волновые функции сосредоточены в области ядра “своего” атома и быстро спадают при удалении от него.
Положим |
Hnn= ; |
n 0 |
cmH m E cm m |
|
|
|
|
|
|
Концевой атом в особом положении |
H = |
/ |
m |
m |
|
|
|||
00 |
|
|
|
|
Hт,n 1=
Hn,m=0; m-n 2
Snm nm
Система из N+1 взаимно зацепляющихся уравнений:
|
|
|
n |
|
n 1 |
n 1 |
|
|
E |
c |
|
c |
c |
|
E / |
c0 |
c1 |
|
||
|
|
|||||
Необходимо найти cn и допустимые значения Е
Граничное условие на другом конце цепочки
Большое число атомов.
Конкретный вид этого условия не скажется на значении волновой функции при n=0.
cN=0
Решение известно  cn=sin [(N-n) ]
cn=sin [(N-n) ]
Действительно  cN=sin[(N-N) ]=0
cN=sin[(N-N) ]=0
 - новая переменная
- новая переменная
|
|
|
n |
n 1 |
n 1 |
|
|
E |
c |
c |
c |
|
E / |
c0 |
c1 |
|
|
|
|
||||
|
|
|
|
|
|
( E- )sin(N-n) = [sin(N-n-1) +sin(N-n+1)]=2 sin(N-n) cos E= +2 cos
Чтобы определить допустимые значения , используем второе
(E- /)sinN = sin(N-1) |
|
|
|
|
( - . / +2 cos )sinN = (sinN cos - cos N sin ) |
|
|
|
|
|
/ |
|
||
Обозначение |
|
z |
|
|
|
|
|
||
Трансцендентное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- z+2cos = cos - sin ctg N |
z=cos +sin ctgN |
|||
|
|
|
|
|
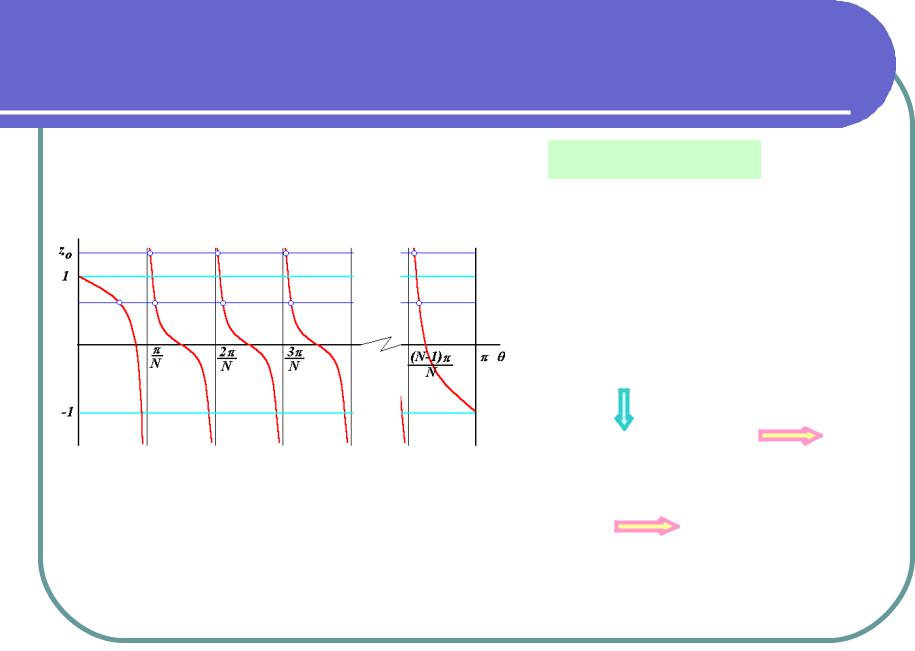
Графическое решение |
|
z=cos +sin ctgN |
|
Введем функцию f( ) = cos +sin ctgN |
|
|
|
|
|
|
|
|
При далеко от границ |
||
|
поведение f( ) определяется |
||
|
котангенсом |
||
|
|
При =0 или требуется особое |
|
|
|
рассмотрение |
|
|
|
|
|
|
|
|
|
Неопределенность |
0 |
|
iim sin |
lim |
|
cos |
|
|
1 |
0 |
|
|
|
1 |
|
N |
|
f(0)=1 и |
f( ) = -1 |
|||||
0 tgN |
0 |
|
|
|
Аналогично |
|||||
|
|
N |
|
|
|
|
|
для = . |
|
|
|
|
cos2 N |
|
|
|
|
|
|
||
Точки, в которых z=f( ), есть решения уравнения
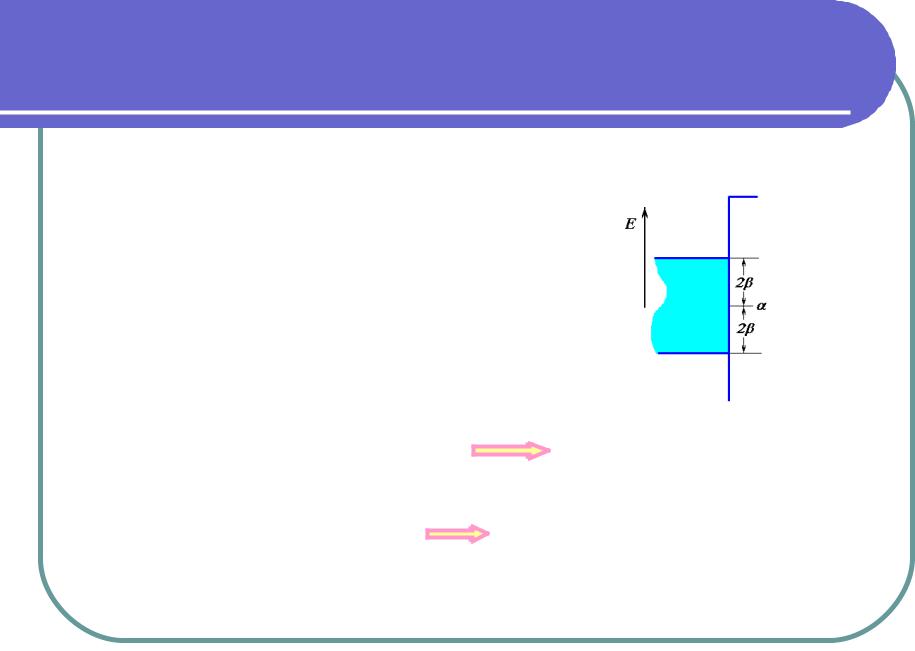
При z <1 имеется N допустимых значений , т.е. столько, сколько и нужно
Волновые функции периодичны,
энергия в интервале: - 2 E +2
Обычная зонная структура
Ширина разрешенной зоны 4
- величина резонансного интеграла, характеризующего взаимодействие между соседними атомами
Чем сильнее атомы связаны друг с другом, тем шире полоса разрешенных состояний.
Наиболее интересен случай z >1 |
Количество решений на одно меньше |
Недостающее решение в области комплексных чисел
Даст ли комплексное решение физически разумный результат? Обязательное условие - реальность энергии
Положим |
= +i , |
где 0 |
Потребуем, чтобы мнимая часть энергии равнялась нулю
ImE=0=Im [ +2 cos( +i )]=2 Im [cos cos(i ) - sin sin(i )]= =2 Im [cos ch - I sin sh ]= - 2 sin sh
Имеющее физический смысл решение возможно при условии
sin =0 |
=k , где k=0,1,2,... |
Функция периодична |
Интерес представляют два значения: =0 или . |
|||
|
Волновая функция |
|
|
|
Второе условие, которому |
cm m |
|
||
ограничена |
|
|||
должно удовлетворять |
|
|||
во всем пространстве |
m |
|
||
решение, |
|
|
||
cт - ограничен |
||||
|
||||
|
|
|||
cт=sin[(N-т)i ]=i sh [(N-т) ]=i [sh N ch т - sh т ch N ]= =i sh N [ch т - cth N shт ]
При больших N |
lim cth x 1 |
cт= i shN [ch т - sh т ]=i sh N e-т |
x |
||
Комплексное решение физически разумно при >0. |
||
Наибольший ст при малых m. |
Экспоненциально спадает |
|
|
|
по мере удаления от концевого атома. |
Электронные состояния, |
Поверхностные состояния |
|
располагающиеся у конца цепочки |
||
|
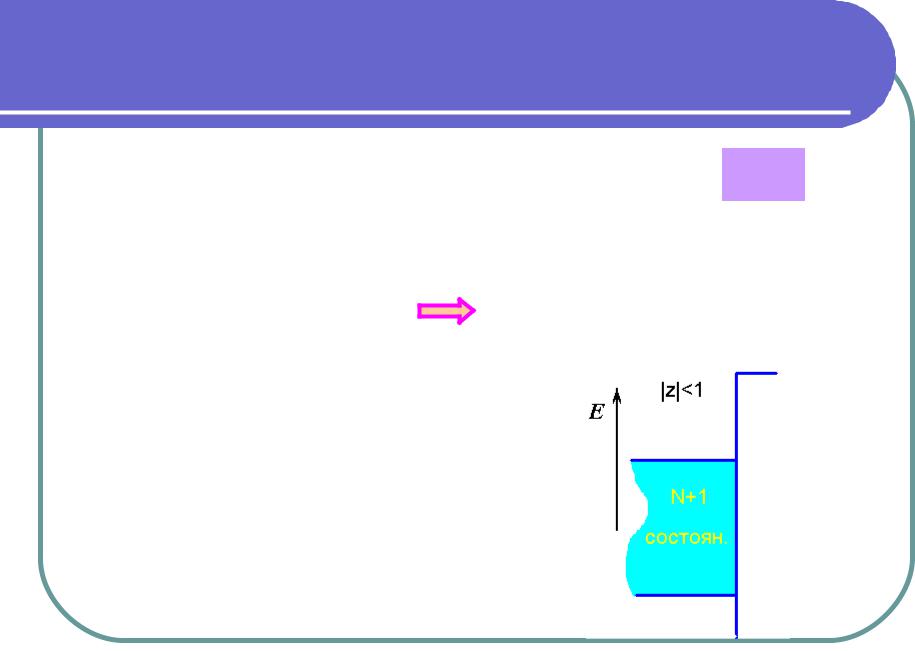
С физической точки зрения. |
|
|
|
|
|
/ |
|
||
Положим Evacuum = 0 |
и / меньше нуля |
z |
|
|
Положим, что и отрицательна. |
|
|
|
|
Если потенциал у атома |
N+1 делокализованных состояний, |
|||
на конце цепочки не отличается |
образуют зону разрешенных состояний |
|||
от объемного, то = / и z=0 |
||||
|
|
|
||
При понижении энергии электрона у концевого атома / уменьшается, z становится больше 0.
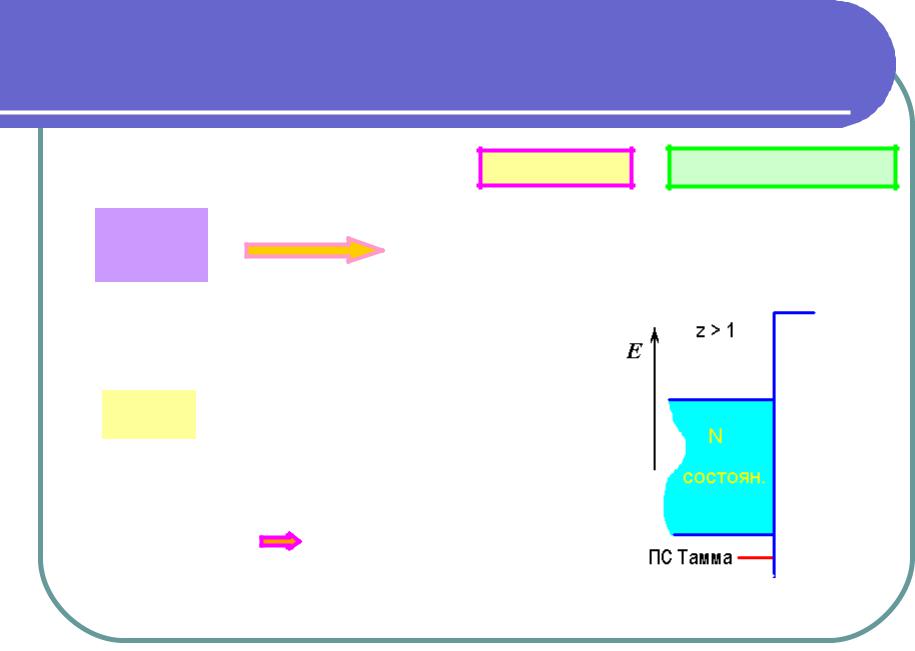
Z превышает 1 |
E= +2 cos |
z=cos +sin ctgN |
|
|
|
/ |
|
|
|
|
|
Соответствует притяжению |
||
|
|
z |
|
|
|
|
|
|||
|
|
|
|
|
|
|
электрона к концевому атому. |
|||
Величина |
|
|
|
N |
|
|||||
z ch |
|
ish |
icthN |
ch sh e |
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
|
|
z e |
|
|
>0 и тем больше, чем больше z |
|||||
E= +2 cos i = +2 ch
и отрицательны, |
Энергия ПС ниже зоны |
||
сh x 1 |
всегда, |
||
разрешенных состояний |
|||
|
|
||
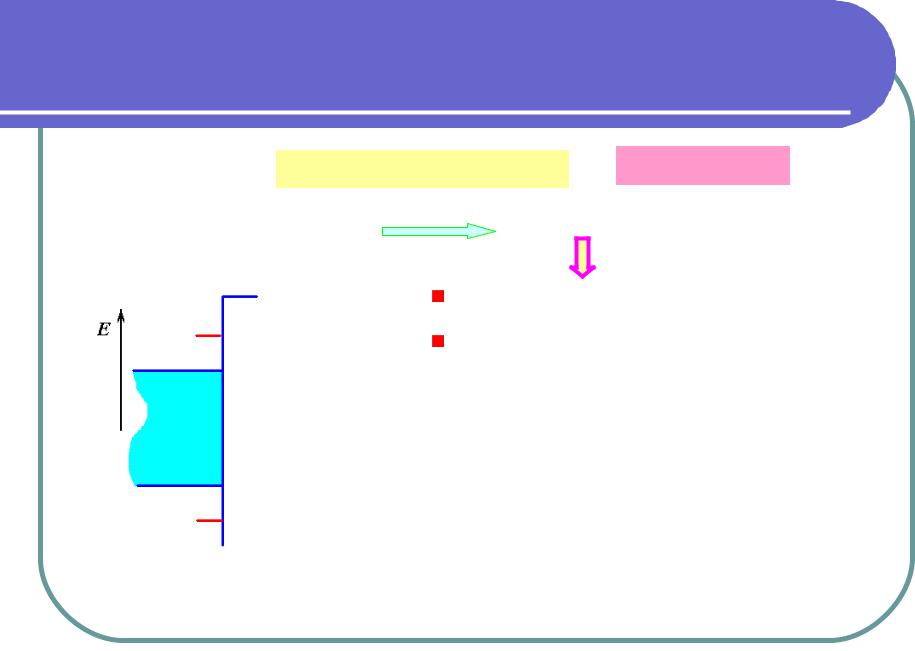
|
|
|
E= +2 cos i = +2 ch |
|
cт= i sh N e-т |
Чем сильнее притяжение |
Тем больше |
|
электрона к концу цепочки |
||
|
||
|
Тем глубже расположен его уровень |
|
|
Тем сильнее локализовано состояние |
|
|
на поверхности. |
Отталкивание электрона от поверхности, также при z >1, также приводит к появлению ПС.
Располагается выше зоны разрешенных состояний
Наличие поверхности может привести к изменению потенциала не только на атоме с т=0, но и на нескольких ближайших к поверхности
