Лекция 8 (Г)

...04.12

5.7. Структура турбулентного потока

П

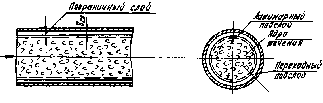
Рис. 5.6

ри турбулентном режиме движения непосредственно у стенок имеется тонкий ламинарный подслой, далее находится переходный подслой. Оба подслоя вместе составляют пограничный слой. За пределами пограничного слоя располагается ядро течения, в котором движение жидкости является уже турбулентным (рис. 5.6).

С

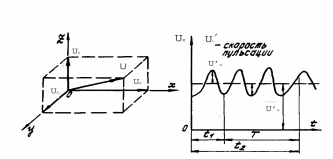
Рис. 5.7

корость и давление в каждой точке турбулентного потока беспорядочно пульсируют около некоторых средних значений (рис. 5.7).

При описании турбулентного потока вместо действительных (мгновенных) значений скорости и давления пользуются осредненными во времени значениями. Например, осредненное значение продольной составляющей скорости в направлении оси x в некоторой точке потока определяется соотношением

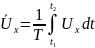, (5.33)

где U_x - продольная составляющая мгновенной скорости; Т=t₂-t₁ - период осреднения.

Действительную (мгновенную) скорость можно представить как сумму осредненной и пульсационной скоростей:

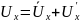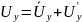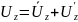; ; . (5.34)

Период осреднения Т необходимо выбирать достаточно большим по сравнению с периодом пульсаций. Подставив в (5.33) выражение (5.34) для U_x, получим

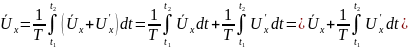. (5.35)

Это означает, что осредненная пульсационная скорость равна нулю:

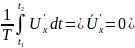. (5.36)

Если величины, осредненные для разных последовательных моментов времени, оказываются постоянными, турбулентное движение считают установившимся.

5.8. Уравнения Рейнольдса

Подставив в уравнения Навье-Стокса (4.29) вместо компонентов скорости их выражения через осредненные и пульсационные скорости для установившегося турбулентного движения, можно получить уравнения Рейнольдса:

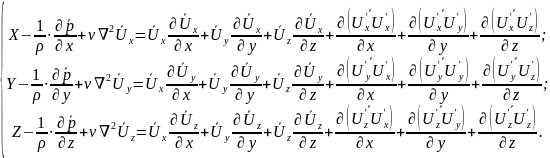(5.37)

В отличие от уравнений Навье-Стокса каждое из уравнений (5.37) включает три дополнительных члена, зависящих от пульсаций скорости. Представив каждый из этих членов в форме 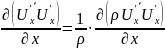, перепишем уравнения Рейнольдса, перенеся члены, зависящие от пульсаций, в левую часть. Ограничимся только первым уравнением

.

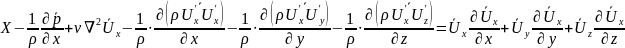Наряду с членами, выражающими действие вязкостных напряжений,

,

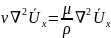уравнения Рейнольдса содержат члены, выражающие действие напряжений, присущих только турбулентному потоку 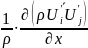, где 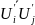- осреднённое произведение пульсационных скоросте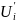й и .

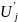Полные касательные напряжения - сумма вязкостных и турбулентных:

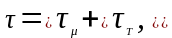(5.38)

_{причем турбулентные обладают свойством взаимности} (τ_ij=τ_ji) и выражаются как

_.

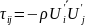5.9. Гипотезы Буссинеска и Прандтля о турбулентных напряжениях

Рассмотрим прямолинейный установившийся турбулентный поток с неравномерным распределением усредненных скоростей (рис. 5.8).

Гипотеза Буссинеска о связи турбулентного напряжения τ_Т с усредненной скоростью :

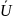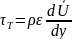
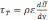, (5.39)

где ε - кинематический коэффициент турбулентной вязкости.

Гипотеза Прандтля - простая модель турбулентного потока, позволяющая установить общие закономерности движения:

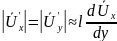
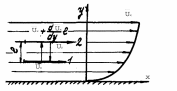
Рис. 5.8

. (5.40)

Следовательно,

.

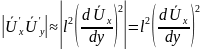Модуль касательного турбулентного напряжения теперь выражается как 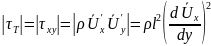, (5.41)

Коэффициент l в (5.40) и (5.41) называют длиной пути перемешивания. Для определения этого понятия допустим, что жидкая частица, имевшая в слое 1 усредненную скорость 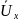(рис. 5.8), под влиянием турбулентной пульсации 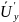перемещается на расстояние l в слой 2, где усредненная скорость равна 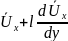. Основное допущение этой гипотезы заключается в том, что путь между слоями 1 и 2 частица проходит без взаимодействия с другими частицами, т. е. так же, как молекула газа проходит путь свободного пробега. Тогда в результате смешения с частицами слоя 2 переместившаяся частица приобретает усредненную скорость этого слоя, т. е. в нем будет иметь место пульсация продольной скорости.

Связь между кинематическим коэффициентом турбулентной вязкости ε и длиной пути перемешивания l устанавливается из сопоставления (5.39) и (5.41):

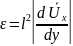. (5.42)

Гипотезы Буссинеска и Прандтля сводят задачу отыскания связи турбулентных касательных напряжений с полем усредненных скоростей к задаче определения функций координат ε и l, характерных для турбулентного потока.

Решения этой второй задачи основаны на экспериментальных данных и на дополнительных гипотезах. Например, Прандтль предположил, что для полуограниченного турбулентного потока вблизи плоской стенки справедлива линейная связь пути перемешивания l и расстояния от стенки y: l= ϰy, где ϰ - универсальная постоянная.