3.7. Поверхностная (проектированная) зона Бриллюэна
Для объема |
Зонная теория |
|
|
Одноэлектронные волновые функции |
|
||
Функции Блоха |
k=uk(r)exp(i(kr)) |
|
|
k - трехмерный волновой вектор |
|
||
uk(r) инвариантна относительно трансляции |
uk(r) = uk(r+Ri) |
||
|
|||
на любой вектор решетки Ri: |
|
|
|
Дисперсионные зависимости (k) |
|
||
Анализ (k) проводят используя понятие зоны Бриллюэна |
|||
Зона Бриллюэна |
Ячейка Вигнера-Зейтца в пространстве импульсов |
||
Физические величины |
Периодические функции |
Состояния с |
|
k и k’=k+G |
|||
по k,период равен |
|||
|
физически |
||
|
вектору обратной решетки G |
||
|
|
эквивалентны |
|
|
|
- /a ki /a |
Можно анализировать зависимость (k) |
|
|
в пределах только первой зоны |
|
|
Нет однозначного соответствия |
|
Приведенная зона |
между волновым вектором и энергией. |
Бриллюэна |
|
Металл со свободными электронами, |
|
|
простая кубическая решетка |
|
|
Зона Бриллюэна - куб с ребрами |
|
|
длиной 2 /a |
|
|
Ряд точек и направлений представляют |
|
|
наибольший интерес |
|
|
Наличие у них элементов симметрии |
|
|
облегчает расчеты. |
|
|
Система обозначений точек и направлений, |
|
|
основанная на теории групп |
|
~ (kx,0,0,) |
~ (0,0,0). |
~ ( /a,0,0) |
|
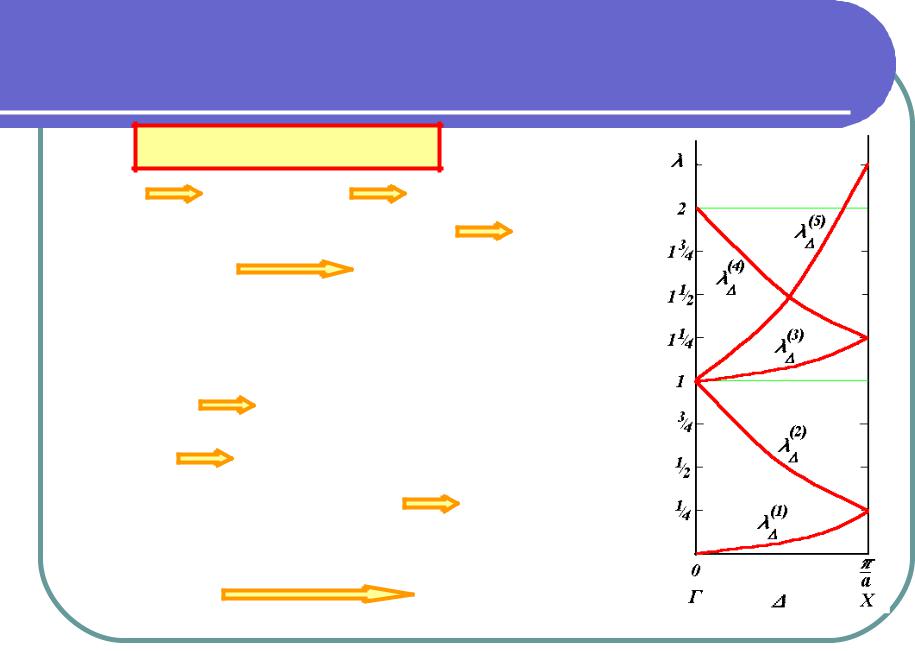
(k) при изменении k вдоль направления [001] ( ) от точки Г до Х.
Уравнение Шредингера |
|
ky=kz=0, 0 kx /a
2
2m
|
= exp (i(k - G)r), |
G = 2 /a(n1 ix |
|
ix , iy, iz - единичные орты |
||||||||
|
+ n2 iy |
+ n3 iz) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
ni - любые целые числа |
|
Будем измерять k в величинах, кратных 2 /a: |
|
|
||||||||||
k = 2 /a( , , ) = 2 /a( ix + iy + iz), |
|
Пределы изменения , , - от 0 до 1/2. |
||||||||||
2 4 |
|
2 |
ny |
2 |
nz |
2 |
|
|
|
|||
|
|
|
2 nx |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
a |
|
|
|
|
|
|
|
2ma2 |
|
|
|
|
Введем безразмерную величину |
|
|
|
4 2 |
||||||
|
|
|
|
|
||||||||
= ( -n1)2+( -n2)2+( -n3)2
= ( -n1)2+( -n2)2+( -n3)2
Точка Г |
0 |
Г = n12+n22+n32 |
||||||
Минимальная энергия при n = (0,0,0) |
|
= 0 |
||||||
Вдоль оси . |
|
|
|
|
|
0 ky kz 0 |
||
Направление [100] |
|
|
|
|
|
|
|
|
Точка X |
|
|
|
Х (n1,n2,n3)= (n1 - 1/2)2 +n22+ n32 |
||||
= (n1- )2+ n22+n32 |
|
|
|
|
|
|
|
|
n = (0,0,0) |
|
|
(1)(0,0,0) = 2 |
и (0,0,0) = 1/4 |
||||
|
|
|
|
Х |
|
|||
n = (1,0,0) |
|
Х(2)(1,0,0) = 1/4 |
(2)=1 |
(2) = (1 - )2 |
||||
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
(3) |
= 2 + 1 |
||
n (0,1,0),(0,0,1),(0,1,0),(0,0,1) |
||||||||
|
|
|
|
|
|
|
|
|
|
(3) |
вырождена четырехкратно. |
||||||
n=(1,1,0) |
|
|
|
|
|
|
|
= (1 - ) +1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
(4) |
2 |
Дисперсионные зависимости |
|
Появление энергетических щелей |
усложняются при учете |
|
|
|
на границах зон Бриллюэна |
|
периодического потенциала |
|
|
|
Понижение кратности вырождения |
|
|
|
|
|
|
Изменение формы дисперсионных |
|
|
зависимостей и т.д. |
Кристалл, ограниченный поверхностью |
Поверхность при z = 0 |
|
Трансляционная симметрия |
|
V(r) = V(u + z) |
сохраняется по координатам x и y |
|
|
|
|
|
= k (z)exp (i(k (x)u), |
u - вектор двумерной поверхностной решетки |
|
k - волновой вектор двухмерной решетки, параллельной поверхности.
Сведение симметрии к двум измерениям равносильно тому, что элементарная ячейка кристалла простирается до бесконечности в направлении, перпендикулярном поверхности
Удобно использовать зону Бриллюэна |
|
Расширяем элементарную |
Длина грани по оси kz (2 /az ) |
ячейку вдоль оси z |
в обратном пространстве уменьшается. |
“Сплющиваем” зону Бриллюэна |
|
ЗБ двумерна, что
В пределе соответствует размерности
“хорошего” квантового числа k
Поверхностная (“проектированная”) зона Бриллюэна
Над обозначениями точек и направлений ставится черта
“Сплющивание” не приводит к изменению спектра объемных собственных состояний с фиксированным k|| и различными k
Для фиксированного значения k
существует не одно дискретное собственное значение E,
а некоторый континуум
Каждому из состояний, находящихся в голубой области может быть сопоставлено по меньшей мере одно объемное состояние.
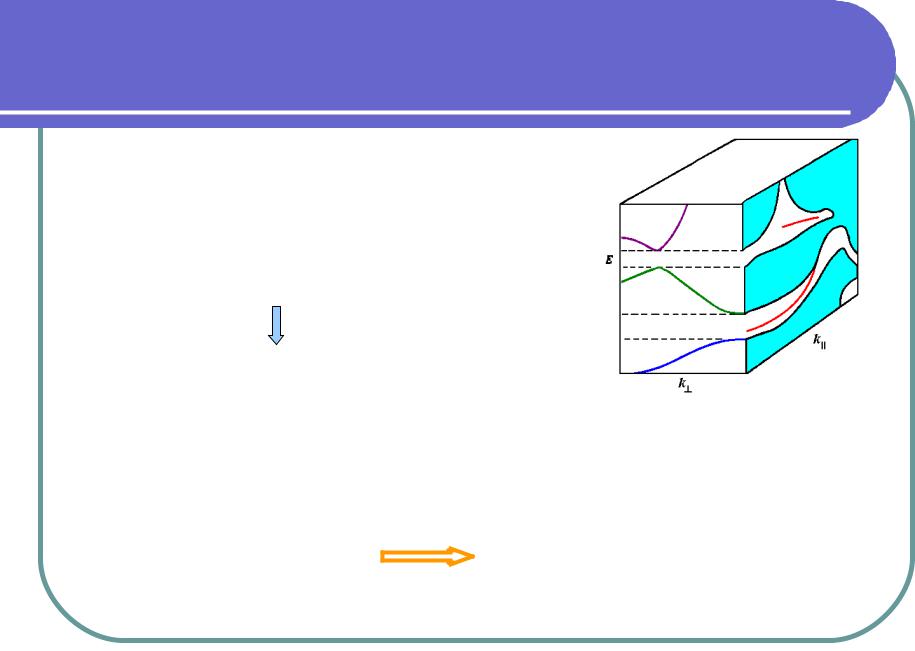
В случае полупроводника или диэлектрика на проекции объемных состояний должен иметься энергетический зазор по всей ПЗБ.
Поверхностные состояния могут существовать для некоторого интервала значений k
Зона поверхностных состояний.
Если в бесконечном кристалла в некотором интервале Е нет разрешенных состояний той же симметрии ни при каком значении k ,
то электроны на ПС локализованы у поверхности
Их волновые функции экспоненциально затухают при удалении от поверхности
как в сторону вакуума, так и в сторону объема
Связанные поверхностные состояния Энергетические уровни -
-связанные поверхностные уровни Связанная поверхностная зона
Если энергетический уровень ПС |
Имеется взаимодействие состояний, |
|
совпадает с собственными |
||
отвечающих одинаковой |
||
значениями бесконечного |
||
собственной энергии |
||
объемного кристалла |
||
|
Возрастает амплитуда у поверхности. При
Резонанс 
удалении вглубь амплитуда убывает, однако значительно медленнее, чем экспоненциально
Резонансные поверхностные состояния
Если собственные значения энергии электронов кристалла с поверхностью совпадают с таковыми для бесконечного кристалла, то соответствующие им волновые функции распространяются в объем кристалла без затухания
Объемные уровни
Если симметрия поверхностного слоя не отличается от имеющейся в объеме
Однако |
Часто наблюдается |
|
реконструкция. |
|
Размеры элементарной |
|
ячейки изменяются. |
Проектирование не сложно
Изменяются величины 
векторов обратной решетки,
размеры зоны Бриллюэна
Si(111)
Идеальная |
ПЗБ - шестиугольник |
|
структура (1x1) |
||
|
Структура (2x1) 
ПЗБ - прямоугольник, вписанный в шестиугольник