Комбінаторика

Комбінаторика – розділ математики, в якому розглядаються комбінаторні задачі, тобто такі, в яких є перестановки, розміщення, комбінації елементів множини (одним словом - сполуки).

Перестановки.

Перестановкою з n елементів називається будь-яка множина у сіх цих елементів для яких указано порядок їх розміщення (з n по n).

Розрізняють перестановку без повторень та з повтореннями, в першій - всі елементи різні, а в другій – елементи можуть повторюватися.

Число перестановок позначають Р_n (без повторень); 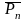(з повтореннями).

Формула для числа перестановок без повторень:

Р_n= n!

Приклад. Запишіть усі перестановки елементів множини: .

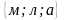Маємо: ; ; ; ; ; .

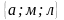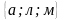Скільки таких перестановок (тобто різних множин)? Р₃=3!=1∙2∙3=6.

Формула для перестановок з повтореннями:

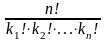= , де k₁+k₂+…+k_n= n.

n – загальна кількість елементів множини серед яких є однакові;

k_1, k_2,…,k_х – число повторень однакових елементів.

Приклад. Запишіть усі перестановки елементів, що складають слово «мама».

Маємо: ; ; ; ; ; .

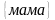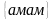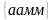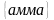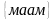Скільки таких перестановок (тобто різних множин)?

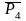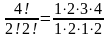= =6 (k₁=2 – два рази повторюють «м», k₂=2 – два рази повторюють «а»).

Задачі.

1. Знайти кількість різних шестизначних чисел, які можна скласти з цифр 1, 2, 3, 4, 5, 6, не повторюючи ці цифри в одному числі.

Розв’язання:

n=6, Р_n=Р₆=6!=1∙2∙3∙4∙5∙6=36∙20=720.

Відповідь: 720 чисел.

2. Знайти кількість різних шестизначних чисел, які можна скласти з трьох двійок, двох сімок і однієї п’ятірки.

Розв’язання:

Маємо: 2;2;2 ; 7;7 ; 5 , тому n=6, k₁=3, k₂=2, k₃=1 (число повторень двійки, сімки, п’ятірки).

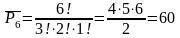
Відповідь: 60 чисел.

Розміщення.

Розміщенням з n елементів по m елементів (m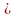 n) називається будь-яка упорядкована множина з m елементів, яка складена з елементів n-елементної множини.

Розміщення бувають без повторень та з повторенням, у першому випадку - всі елементи різні, а в другому випадку однакові.

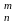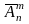Число розміщень позначають A (без повторень); (з повтореннями).

Формула для числа розміщень без повторень:

A =

Приклад. Запишіть усі розміщення з елементів множини 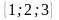по два елементи, якщо цифри не можуть повторюватися.

Маємо: .

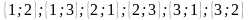Скільки таких розміщень (тобто різних множин)? ( ).

Маємо: А =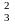

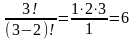
Формула для числа розміщень з повтореннями:

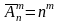, n – загальна кількість елементів множини; m – кількість елементів нової множини.

Приклад. Запишіть усі розміщення з елементів множини по два елементи, якщо цифри можуть повторюватися.

Маємо: .

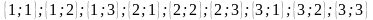Скільки таких розміщень (тобто різних множин)? n=3; m=2; .

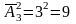Задачі.

1. Розклад на день містить 6 уроків. Знайти кількість варіантів можливого розкладу за умови, що жоден з 10 навчальних предметів не стоїть у ньому двічі.

Розв’язання:

n=10; m=6; А =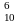

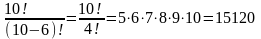
Відповідь: 15120 варіантів розкладу.

2. Нехай є сейф, у якому використовуються 5 дисків, а на кожному диску є 12 букв. Скільки невдалих спроб може бути зроблено людиною, яка не знає секретного слова та добирає його навмання?

Розв’язання:

Маємо: n=12; m=5; якщо дія виконується навмання, то з’являються повторення тому

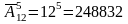
Відповідь: 248832 спроби.

Комбінації (сполучення).

Комбінацією без повторень з n елементів по m елементів ( ) називається неупорядкована m-елементна підмножина n- елементної множини.

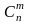- число комбінацій без повторень.

Формула для числа комбінацій без повторень:

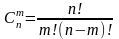
Приклад. Запишіть усі комбінації з елементів множини по два елементи.

Маємо: .

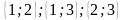Скільки таких комбінацій (тобто різних множин)? ( ).

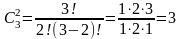
Нехай є n елементів (не обов’язково різних) неупорядкованої множини. Комбінаціями з n елементів по m елементів з повтореннями називають такі неупорядковані множини, до кожної з яких входять m елементів і які відрізняються лише складом елементів (хоч би одним).

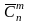- число комбінацій з повторенням.

Формула для числа комбінацій з повторенням:

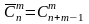
Приклад. Запишіть усі комбінації з елементів множини 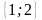по три елементи.

Маємо: .

Скільки таких комбінацій (тобто різних множин)? n=4; m=7; .

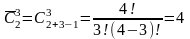Задачі.

1. Скількома способами можна вибрати трьох чергових у класі, де навчаються 20 учнів?

Розв’язання:

Маємо: n=20; m=3;

Відповідь: 1140 способів.

2. У продажу є квіти чотирьох сортів, то скільки можна скласти різних букетів з 7 квіток?

Розв’язання:

Маємо: n=4; m=7;

Відповідь: 120 букетів.