vk.com/club152685050

§2. Примеры решения задач

Пример 1.

Окружность задана общим уравнением x2 + y2 + 6x 8y 11 = 0. Найти координаты центра и радиус этой окружности.

Решение.

Приведем данное уравнение окружности к каноническому виду, для этого выделим полные квадраты по переменным x и y соответственно. Будем иметь:

x2 y2 6x 8y 11 x2 6x 9 y2 8y 16 9 16 11x 3 2 y 4 2 36 0.

Написать уравнение окружности, проходящей через точки А(5, 0) и В(1, 4), если ее центр лежит на прямой x + y 3 = 0.

Решение.

Найдем координаты точки М - середины хорды АВ.

Имеем xм = (5 + 1) / 2 = 3, yм = (4 + 0) / 2 = 2, то есть М(3, 2). Центр окружности лежит на серединном перпендикуляре к отрезку АВ.

Уравнение прямой АВ имеет вид: (y 0) / (4 0) = (x 5) / (1 5), то

есть x + y 5 = 0. Так как угловой коэффициент прямой АВ равен 1, то угловой коэффициент перпендикуляра к ней равен 1, а уравнение

этого перпендикуляра: y 2 1 x 3 , то есть x y 1 = 0. Центр искомой окружности С есть точка пересечения прямой АВ с указанным перпендикуляром, то есть координаты центра определяются путем

решения системы уравнений x + y 5 = 0, x y 1 = 0. Следовательно, x = 2, y = 1, то есть С (2, 1). Радиус окружности

23

vk.com/club152685050

Пример 3.

Большая ось эллипса равна 12, а директрисами этого эллипса

служат прямые x = 12. Найти уравнение эллипса и его эксцентриситет.

c2, а с можно найти, использовав уравнения директрис эллипса x = a2 / c. Взяв первую директрису, получим a2 / c = 12, откуда с = a2 / 12,

с = 36 / 12 = 3, с = 3; b2 = 36 9 = 27, b2 = 27.

Имеем уравнение эллипса х2 / 36 + y2 / 27 = 1. Эксцентриситет эллипса= с / а, = 3 / 6 = 0,5.

Ответ: х2 / 36 + y2 / 27 = 1, = 0,5.

Пример 4.

На эллипсе х2 / 25 + y2 / 16 = 1 найти точку, расстояние которой от правого фокуса в четыре раза меньше расстояния от левого фокуса.

Решение.

Из уравнения эллипса: а2 = 25, b2 = 16, поэтому a = 5, b = 4;

с2 = a2 b2 = 25 16 = 9, с = 3, эксцентриситет = с / а = 3 / 5. Расстояние до фокусов вычисляется по формулам:

r1 = a + x = 5 + (3 / 5) x, r2= a x = 5 (3 / 5) x.

По условию r1 = 4r2; следовательно, х = 5. Подставляя это значение в уравнение эллипса, получим y = 0. Искомая точка М (5, 0).

Ответ. Точка М (5, 0).

Пример 5.

Написать уравнение касательной к эллипсу х2 / 30 + y2 / 24 = 1, параллельной прямой 2x y + 17 = 0.

24

vk.com/club152685050

Решение.

Поскольку касательная параллельна прямой 2x y + 17 = 0, то ее угловой коэффициент k = 2, тогда ее уравнение можно записать в виде y = 2x + C. Значение С определим из условия касания прямой эл-

липса. Учитывая, что а2 = 30, b2 = 24, А = 2, В = 1, будем иметь:

А2а2 + В2b2 = C2, откуда 4 · 30 + 1 · 24 = С2, и С = 12. Следовательно, условию задачи удовлетворяют две касательные:

y = 2x + 12, y = 2x 12.

Ответ. Уравнение касательных: y = 2x + 12, y = 2x 12.

Пример 6.

Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы 9x2 16y2 = 144.

Решение.

Приведем данное уравнение к каноническому виду, для чего необходимо разделить обе его части на 144. Выполняя деление, получим

х2/ 16 y2/ 9 = 1. Теперь можем выписать а2 = 16, b2 = 9. Таким образом, а = 4 есть действительная полуось, b = 3 - мнимая полуось.

Далее c a2 b2 16 9 5, фокусы: F1 ( 5, 0), F2 (5, 0). Эксцентриситет

a) x, в нашем случае y = (3 / 4) x. Уравнения директрис находятся из

Пример 7.

Составить уравнение гиперболы, зная, что расстояние между ее

вершинами равно 8, а фокусы находятся в точках F1 ( 3, 3) и F2 (7, 3). Решение.

Так как по условию ординаты фокусов равны 3, то фокусы гиперболы лежат на прямой y = 3, следовательно, центр гиперболы также находится на прямой y = 3 и делит расстояние между фокусами F1 F2

пополам. Таким образом: x0 = ( 3 + 7) / 2 = 2, y0 = 3, координаты центра гиперболы М(2, 3). Далее, согласно условию 2а = 8, тогда а = 4 и

25

vk.com/club152685050

Пример 8.

К гиперболе х2 / 8 y2 / 9 = 1 провести касательные через точку N(2, 0).

Решение.

Точка N(2, 0) гиперболе не принадлежит, поэтому непосредственно формулой уравнения касательной пользоваться нельзя. Уравнение

C = 2k, a2 = 8, b2 = 9. Подставим значения постоянных в формулу, получим 8k2 9 = 4k2, откуда k = 3 / 2. Следовательно, условию задачи удовлетворяют две прямые y = (3 / 2) (x 2).

Ответ. Уравнение касательных: 3x + 2y + 6 = 0 и 3x + 2y 6 = 0.

Пример 9.

Найти координаты фокуса и уравнение директрисы параболы y2 = 8x. Вычислить длину фокального радиуса точки М(2, 4).

Решение.

Парабола задана каноническим уравнением y2 = 2рx. Следовательно, 2р = 8, р = 4. Тогда координаты фокуса F(2, 0), уравнение дирек-

трисы: х = 2. Длину фокального радиуса точки М( 2, 4) вычислим по формуле: r = x + p / 2 = 2 + 2 = 4.

Ответ: F(2, 0), х = 2, r = 4.

Пример 10.

Написать уравнения параболы и ее директрисы, если парабола проходит через точки пересечения прямой x + y = 0 и окружности

x2 + y2 4x = 0 и симметрична относительно оси OY.

Решение.

Найдем точки пересечения заданных прямой и окружности, для этого решим совместно уравнения:

26

vk.com/club152685050

Точки пересечения О(0, 0) и А(2, 2). Так как парабола проходит через начало координат О(0, 0) и симметрична относительно оси OY, то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид: х2 = 2рy. Так как парабола проходит через

точку А(2, 2), то координаты этой точки удовлетворяют уравнению параболы: 22 = 2р ( 2), 4р = 4, р = 1. Таким образом, уравнением параболы будет: х2 = 2y. Уравнение директрисы: y = p / 2, так как р = 1, то y = 1 / 2 или 2y 1 = 0.

Ответ: х2 = 2y, 2y 1 = 0.

Пример 11.

Составить уравнение геометрического места точек, одинаково

удаленных от точки F( 2, 0) и от прямой х + 6 = 0. Найти точки пересечения этой кривой с осями координат.

Решение.

Обозначим произвольную точку искомой кривой через P(x, y), ее

расстояние от точки F( 2, 0) равно: PF x 2 2 y2 ; расстояние до прямой х + 6 = 0 находится как d = x + 6. Так как по условию d = PF, то приравняв их, получим уравнение: x 6 x 2 2 y2 . Возводя в квадрат обе части этого уравнения и произведя необходимые упрощения, получим уравнение y2 = 8x + 32 или y2 = 8 (x + 4). Полученное уравнение есть уравнение параболы, симметричной относительно оси ОХ.

Вершина ее находится в точке А( 4, 0). Точки пересечения параболы

Пример 12.

Составить уравнение окружности, касающейся двух параллельных

прямых 2x + y 5 = 0 и 2x + y + 15 = 0, причем одной из них в точке А(2, 1).

Решение.

Определим диаметр окружности, для чего используем формулу расстояния от точки до прямой. Уравнение прямой 2x + y + 15 = 0,

27

vk.com/club152685050

точка А(2, 1), поэтому d 2 2 1 1 15 / 4 1 20 / 5 45 , тогда радиус окружности r 2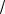5 . Так как искомая окружность проходит через точ-

ку А(2, 1), то ее уравнение имеет вид: (2 xc)2 + (1 yc)2 =20, где С(хс, yc) - центр этой окружности. Для нахождения неизвестных хс, yс запишем второе уравнение, определив расстояние от точки С до первой прямой, причем, поскольку точка С лежит по одну сторону от прямой вместе с началом координат, то это расстояние будет со знаком минус: 25 2xc yc 5 / 5. Решая совместно полученные два уравнения,

находим: xc = 2, yc = 1.

Ответ. Уравнение окружности (x + 2)2 + (y + 1)2 = 20.

Пример 13.

Составить уравнение параболы, симметричной относительно оси ОХ, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной оси ОХ, равна 16, а расстояние этой хорды от вершины равно 6.

Решение.

Так как известны длина хорды и расстояние ее от вершины, то, следовательно, известны координаты конца этой хорды - точки М, лежащей на параболе. Уравнение параболы имеет вид y2 = 2px; полагая в нем x = 6, y = 8, находим 82 = 2р · 6, откуда 2р = 32/ 3.

Ответ. Уравнение искомой параболы y2 = (32/ 3)x.

Решение типового задания.

1.Найти угловой коэффициент прямой и отрезок, отсекаемый ею на оси ординат, если прямая проходит через точки А(2; -8) и В(-1; 7).

Решение. Уравнение прямой, проходящей (на плоскости) через две заданные точки:

Подставляя наши значения, получаем:

y 5x 2 .

Значит, угловой коэффициент равен -5, а отрезок, отсекаемый на оси ординат равен 2.

28

vk.com/club152685050

2. Провести через точку M(-1;4) прямую, отстоящую от точки Q(-2;-1) на расстояние 5.

Решение. Расстояние от искомой прямой y Ax C 0 до нашей точки

Q равно

3.Даны координаты вершин пирамиды ABCD: A(3; 5; 4), B(8; 7; 4), C(5; 10; 4), D(4; 7; 8). Найти уравнения ребер AB, BC, CD и угол ABС

Решение. Уравнения ребер можно написать, выписав уравнение прямой, проходящей (в пространстве) через 2 заданные точки:

Для того, чтобы найти угол ABC найдем направляющие вектора сторон BA и BC:

4. Через точку (1; 5; -1) провести прямую, перпендикулярную прямым x+1=y/3=-z-2 и x=2-3t, y=-1+t, z=-2t.

Решение. Направляющие вектора этих прямых равны соответствен-

5.Вычислить угол между плоскостями 4x - 5y + 3z - 1 = 0 и x -4y - z + 9 =0.

29

vk.com/club152685050

Решение. Вектор нормали к первой плоскости: N1 (4, 5,3) , ко второй плоскости: N 2 (1, 4, 1) . Тогда угол между ними ( и одновременно

угол между плоскостями) равен:

6.Дан тетраэдр A(-1; 2; 5), B(0; -4; 5), C(-3; 2; 1), D(1; 2; 4). Написать уравнение плоскости, проходящей через вершину D и перпендику-

лярной стороне BC.

Решение. Направляющий вектор стороны BC равен: N1 ( 3,6, 4) .

Этот вектор одновременно является нормалью к искомой плоскости.

Уравнение искомой плоскости A x x0 B y y0 C z z0 0 или, в нашем случае,

3 x 1 6 y 2 4 z 4 0 .

7.Даны вектора a=(3;1;2), b=(2;7;4), c=(5;-8;10). Вычислить вектор (a,b)c

Решение.

(a,b)=6+7+8=21, тогда (a,b)c=21c=(105,-168,210).

8.Найти угол между двумя биссектрисами плоских углов прямого трехгранного угла.

Решение. Выпишем направляющие вектора биссектрис клоских углов прямого трехгранного угла (достаточно только двух в силу симметрии). Это вектора e1=(1,1,0) и e2=(0,1,1). Тогда угол между ними равен

10.Написать уравнение эллипса, проходящего через точки А(6; - 3) и B(- 4;2 6 ).

Решение. Каноническое уравнение эллипса:

x2 / a2 y2 / b2 1.

Подставляя в него наши точки, получаем два уравнения для двух неизвестных 1/ a 2 , 1/ b2 :

36 / a2 9 / b2 1, 16 / a2 24 / b2 1.

30

vk.com/club152685050

Решая, находим искомое уравнение эллипса:

5x2 / 240 y 2 / 36 1.

Индивидуальные задания по аналитической геометрии

Задание 1.

1.Составить уравнение прямой, проходящей через точку А (-3,4) и параллельной прямой x-2y+5=0.

2.Составить уравнение биссектрисы острого угла между прямыми 4y=3x и 5x+12y=10.

3.Даны координаты вершин пирамиды: A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0). Найти уравнения высоты, опущенной из вершины D на грань АВС.

4.Даны две вершины параллелограмма ABCD: C(- 2; 3; - 5) и D(0; 4; -

7)и точка пересечения диагоналей М(1; 2; - 3,5). Найти уравнения стороны АВ.

5.Написать уравнение плоскости, проходящей через точку Р(7; -5; 1) и отсекающей на осях координат равные положительные отрезки.

6.Написать уравнение плоскости. проходящей через точки М(1; 2; 0) и N(2; 1; 1) перпендикулярно плоскости - x + y - 1 = 0.

31

vk.com/club152685050

7.Даны два вектора a(3; -1; 5), b(1; 2; -3). Найти вектор x, перпендикулярный оси OZ и удовлетворяющий условиям (x,a)=9, (x,b)=-4.

8.В параллелограмме ABCD обозначены AB = a, AD = b. Выразить через a и b векторы MA, MB, MC, MD, где М - точка пересечения диагоналей параллелограмма

9.Составить уравнение эллипса, если даны точка эллипса ( 25 ;2) и

его малая полуось b=3.

1. Составить уравнение прямой, проходящей через точку А (-3,4) и

2. На прямой x+2y=12 найти точки, равноудаленные от прямых x+y=5, 7x-y=11.

3. Даны координаты вершин пирамиды А(4; 4; 10), В(4; 10; 2), C(2; 8; 4), D(9; 6; 9). Найти уравнения высоты, опущенной из вершины D на грань АВС

4. Показать, что прямая x=(y-1)/3=(z+2) параллельна плоскости x- 2y+5z=6.

5. Написать уравнение плоскости проходящей через точку Р(-1; 5; -7) и отсекающей на осях координат равные отрицательные отрезки.

6. Написать уравнение плоскости. проходящей через точки М(0;1; 1) и N(2; 0;1) перпендикулярно плоскости 2 x - y + z + 1 = 0.

32

vk.com/club152685050

7.Даны вектора p=(3;-2;1), q=(-1;1;-2), r=(2;1;-3). Разложить c=(11;- 6;5) по базису векторов p,q,r.

8.AD, BE и CF - медианы треугольника ABC. Доказать, что сумма этих векторов равна нулю.

9.Составить уравнение эллипса, если даны точка эллипса ( 2;2) и

его большая полуось a=4.

10.Определить точки пересечения прямой 3x+4y-12=0 и параболы

y 2 9x .

Задание 3.

1.Составить уравнение прямой, проходящей через точку А (-3,4) и параллельной прямой x=2.

2.Написать уравнение прямой, проходящей через точку (1;-4) и равноотстоящей от точек (3;4), (3;-1).

3.Даны координаты вершин пирамиды: A(3; 5; 4), B(8; 7; 4), C(5; 10; 4), D(4; 7; 8). Найти уравнения высоты, опущенной из вершины D на грань АВС

4.Показать, что прямая x-1=y/3=z-1 лежит в плоскости x-2y+5z=6.

5.Три грани тетраэдра, расположенного во втором октанте, совпадают с координатными плоскостями. Написать уравнение четвертой грани, зная длину ребер, его ограничивающих: АВ = 6, ВС = 290,5, СА = 5.

6.Написать уравнение плоскости, проходящей через ось OZ и образующей с плоскостью 2x + y - 50,5z - 7 = 0 угол 60 градусов.

33

vk.com/club152685050

7.Вычислить внутренний угол при B у треугольника A(-1;-2;4), B(- 4;-2;0), C(3;-2;1).

8.Задан тетраэдр OABC. Выразить вектор DE, где D и E середины ребер ОА и ВС, через векторы, совпадающие с ребрами из вершины О.

9.Составить уравнение эллипса, если даны 2 точки эллипса (4; 3 ) ,

(22 ;3) .

10.Определить точки пересечения прямой 3x-2y+6=0 и параболы

y 2 6x .

Задание 4.

1.Составить уравнение прямой, проходящей через точку А (-3,4) и параллельной прямой y=-1.

2.Составить уравнение биссектрисы острого угла между прямыми 3y=4x и 5x+12y=10

3.Даны координаты вершин пирамиды: А(3; 5; 4), В(8; 7; 4), С(5; 10; 4), D(4; 7; 8). Найти уравнения высоты, опущенной из вершины D на грань АВС

4.Доказать, что прямая (x+2)/3=(y+1)/(-2)=z параллельна прямой

x+y-z=0, x-y-5z-8=0.

5.Три грани тетраэдра, расположенного в третьем октанте, совпадают с координатными плоскостями. Написать уравнение четвертой грани, зная длину ребер, его ограничивающих: АВ = 290,5, ВС = 5, СА = 6.

6.Через точку (2; 3; 4) провести плоскость, перпендикулярную прямой 2x-y+4z+9=0, x+2y-z+3=0.

7.Даны вектора a=(3;-1), b=(1;-2), c=(-1;7). Разложить p=a+b+c по базису векторов a,b.

34

vk.com/club152685050

8. Вычислить углы треугольника A(2; 1; 2 ), B(1; 0; 0), C(1+ 3 ; 3 ;

- 6 ).

9.Составить уравнение эллипса, если даны точка эллипса (15 ; 1)

расстояние между фокусами 2c=8.

10.На параболе y 2 16x найти точки, фокальный радиус которых

равен 13.

Задание 5.

1.Составить уравнение прямой, проходящей через точку А (-3,4) и параллельной прямой x=3+t, y=4-7t

2.Найти угол между прямыми x=7 и y=2x+8

3.Написать уравнения перпендикуляра, опущенного из точки Р(3; -2; 4) на плоскость 5x + 3y - 7z + 1 = 0

4.Через точку (1;5;-1) провести прямую, перпендикулярную прямым:

5. Вычислить расстояние плоскости 15x - 10y + 6z - 190 = 0 от начала координат.

6.Показать, что плоскости x-y+z+1=0, 2x-y-3z=2, 4x-3y=z пересекаются по одной прямой.

7.Вычислить угол между диагоналями четырехугольника A(1;-2;2), B(1;4;0),C(-4;1;1),D(-5;-5;3).

8. Заданы векторы a = 2i + 3j, b = -3j -2k, c = i + j - k. Найти координаты вектора a - 1/2b + c.

35

vk.com/club152685050

9. Составить уравнение эллипса, если даны точка эллипса (2; 5 /3) и его эксцентриситет 2 /3 .

10. Вычислить фокальный радиус точки M параболы y 2 12x , если

ордината этой точки равна 6.

Задание 6.

1.Составить уравнение прямой, проходящей через точку А(-3,4) и перпендикулярной прямой x-2y+5=0

2.Составить уравнение биссектрисы острого угла между прямыми

x-7y=1 и x+y=-7

3.Написать уравнения перпендикуляра, опущенного из точки M(2; - 4; -3) на плоскость 3x - 7y + 5z + 3 = 0

4.Доказать, что прямые

5.Написать уравнение плоскости, проходящей через эти прямые.

6.Для пирамиды с вершинами A(-1; 2; 3), B(3; 3; 6), C(5; 1; 3), D(1; 7; 4) вычислить угол между гранями ABC и ABD.

7. Дан треугольник A(2;1; 2 ), B(1;0;0), C(1 3 ; 3 ; 6 ) . Найти угол при

вершине A.

8.Вне плоскости параллелограмма ABCD взята точка О. Разложить по векторам OA, OB, OC вектор OK, где К - середина стороны AD.

36

найти ее расстояния от фокусов (фокальные радиусы).

3.Написать уравнения ребер тетраэдра с вершинами в точках A(0; 0; 2), B(4; 0; 5), C(5; 3; 0), D(-1; 4; - 2).

4.Написать параметрические уравнения прямой

x+2y+z-1=0, x-y+1=0

5. Вычислить расстояние от плоскости 2x - y + 2z - 90 = 0 до начала координат.

6.Даны точки A(4; -5; 2) и B(-2; 3; 2). Провести через середину отрезка AB плоскость, перпендикулярную ему.

7.Даны вектора a=(3;-2), b=(-2;1), c=(7;-4). Разложить c по базису векторов b,a.

8.Доказать, что треугольник ABC, A(1; 1; 1), B(5; 3; 0), C(2; 0; 1) прямоугольный.

37

фокуса равно 5/2.

10.Через точку М(2; 1) проведена хорда параболы y 2 4x , которая де-

лится в этой точке пополам. Найти ее уравнение.

Задание 8.

1.Составить уравнение прямой, проходящей через точку А(-3,4) и перпендикулярной прямой x=2

2.Составить уравнение биссектрисы острого угла между прямыми 3y=4x и 4y=3x

3.Координаты вершин пирамиды ABCD: A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0). Найти уравнения ребер AB, BC, CD и угол АВС.

4.Вычислить угол между прямыми

5.Найти уравнение плоскости, зная, что точка Р(3; -6; 2) служит основанием перпендикуляра, опущенного из начала координат на эту плоскость

6.Вычислить расстояние между плоскостью 3x+4y+12z=5 и прямой (x-1)/ 4=(y-2)/3=-z/2.

7. Дан треугольник A(2;1; 2 ), B(1;0;0), C(1 3 ; 3 ; 6 ) . Найти угол при

вершине A.

38

vk.com/club152685050

8.Доказать, что сумма векторов, соединяющих центр правильного треугольника с его вершинами, равна нулю.

9.Вычислить фокальные радиусы точки M(-4;12/5), лежащей на эллипсе

x2 y2 1 25 16

10.Вычислить длину хорды, проведенной через фокус параболы y 2 2px перпендикулярно к ее оси.

Задание 9.

1.Составить уравнение прямой, проходящей через точку А(-3,4) и перпендикулярной прямой y=-1

2.Составить уравнения прямых, проходящих через точку (3; 1) и образующих с прямой 3x=y+2 угол в 45 градусов.

3.Вершины пирамиды ABCD имеют координаты A(4; 4; 10), B(4; 10; 2), C(2; 8; 4), D((9; 6; 9). Найти уравнения ребер AB, BC, CD и угол ABС.

4.Найти расстояние от точки (7; 9; 7) до прямой (x-2)/4=(y-1)/3=z/2.

5.Найти уравнение плоскости, зная, что точка Р(-2; -3; 6) служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.

6.Написать уравнение плоскости, проходящей через точку (1; 4; 4) и прямую 4x-3y+5z+6=0, 2x+y-z-2=0.

7.Дан треугольник A(2;1; 2 ), B(1;0;0), C(1 3 ; 3 ; 6 ) . Найти угол при

вершине C.

39

vk.com/club152685050

8.Даны три некомпланарных вектора a, b, и c. Доказать, что векторы a +2b-c, 3a -b +c, -a+5b-3c компланарны.

9.Найти точки пересечения прямой x+2y-7=0 и эллипса x2 4y 2 25 .

10.Составить уравнение параболы, симметричной относительно оси ординат, с вершиной в начале координат и фокусом F(0; 2).

Задание 10.

1.Составить уравнение прямой, проходящей через точку А(-3,4) и перпендикулярной прямой x=3+t, y=4-7t

2.Написать уравнение прямой, удаленной на 5 от прямой 12x+5y=39.

3.Даны координаты вершин пирамиды ABCD: A(4; 6; 5), B(6; 9; 4), C(2; 10; 10), D(7; 5; 9). Найти уравнения ребер AB, BC, CD и угол АВС.

4.Найти проекцию точки (2; 4; 5) на прямую 2x-y+2z-7=0, 3x+4z-9=0.

5.Вычислить расстояние от точки Р(4; 3; -2) до плоскости 3x - y + 5z + 1 =0.

6.Дан тетраэдр A(-1; 2; 5), B(0; -4; 5), C(-3; 2; 1), D(1; 2; 4). Написать уравнение плоскости, проходящей через вершину D и перпендикулярной стороне AB.

7.Даны вектора a=(3;-2), b=(-2;1), c=(7;-4). Разложить b по базису векторов a,c.

8.Вычислить углы четырехугольника A(4; 0; 8), B(5; 2; 6), C(3; 1; 4), D(2; - 1; 6).

40