27. Закон больших чисел. Неравенство Чебышева.

Для любой случайной величины x, имеющей M и D вероятность того, что абсолютная величина отклонения случайной величины от его математического ожидания превосходит некоторое число не больше

P ( | x – M(x)| )

Доказательство:

Рассмотрим новую случайную величину =

Примерим неравенство Маркова

P )

(

M((x –

P ( | x – M(x)| > )

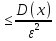
P ( |x – M (x)|

28. Закон больших чисел. Теоремы Чебышева.

Если дисперсии n независимых случайных величин , ­­ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий

Доказательство:

Неравенство Чебышева

p ( |

M (

D () =

p ( |

=

Следствие

Если независимые случайные величины имеют одинаковые M(x) и их D(x) ограничены одной и той же константой, то для любого числа справедливо равенство:

29. Закон больших чисел. Теорема Бернулли.

Частость события n при повторных независимых испытаний в каждом из которых событие происходит с одной и той же вероятностью p, при неограниченном увеличении n, сходится по вероятности p этого события

• Введем индекаторные значения для события а

,

=

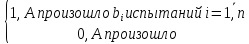
		1	0
		p	1-p-q

M) = p D() = pq

Замечание

Для индикаторов события А справедлива оценка

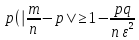
30. Понятие многомерной случайной величины. Двумерная случ величины. Условные законы распред.

Результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин , ….,,которую называют также многомерной (n-мерной) случайной величиной или случайным вектором .

Многомерная случайная величина есть функция элементарных событий :

Случайные величины , входящие в систему, могут быть как дискретными, так и непрерывными.

Двумерная случайная величина и её закон распределения

Определение. Если на одном и том же пространстве элементарных событий заданы две случайные величины Х и Y, то говорят, что задана двумерная случайная величина (Х,Y).

Определение. Законом распределения дискретной двумерной случайной величины (Х,Y) называется таблица

			…
…

Здесь ; .

Условные законы распределения

Условным законом распределения одной из одномерных составляющих двумерной случайной величины называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в какой-то интервал).

Для дискретных случайных величин

Аналогично условное распределение случайной величины Y.

В случае непрерывных случайных величин необходимо определить плотности вероятности условных распределений и . С этой целью в приведенных формулах заменим вероятности событий их «элементами вероятности», после сокращения получим:

*т.е. Условная плотность вероятностей одной из одномерных составляющих двумерной случайной величины равна отношению ее совместной плотности к плотности вероятности другой составляющей.

Теорема умножения плотностей распределений

Условные плотности вероятностей