14. Формула Пуассона.

Теорема. Если вероятность p наступления события A в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний n , причем произведение np стремится к постоянному числу , то вероятность того, что событие A появится m раз в n независимых испытаниях, удовлетворяет предельному равенству:

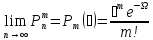
Доказательство.

, np = ƛ, p =

=

=

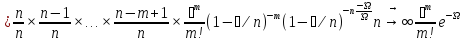
15. Локальная теорема Лапласа.

Если вероятность  появления случайного события  в каждом испытании постоянна, то вероятность  того, что в  испытаниях событие  наступит ровно  раз, приближённо равна:  , где .

При этом, чем больше , тем рассчитанная вероятность  будет лучше приближать точное значению , полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество  испытаний – примерно 50-100, в противном случае результат  может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность  ближе к 0,5, и наоборот – даёт существенную погрешность при значениях , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы  является выполнение неравенства  ().

16. Интегральная теорема Лапласа.

Если вероятность  появления случайного события  в каждом испытании постоянна, то вероятность  того, что в  испытаниях событие  наступит не менее  и не более  раз (от  до  раз включительно), приближённо равна:

, где 

При этом количество испытаний, разумеется, тоже должно быть достаточно большими вероятность  не слишком мала/велика (ориентировочно ), иначе приближение будет неважным либо плохим. 

17. Определение случайной величины. Операции над случайными величинами.

Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, заранее не известно, какое именно (это зависит от случая).

Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4).      Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называетсянепрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.      Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называютсмешанной.

Определим математические операции над ДСВ.

Произведением kX случайной величины Х на постоянную величину k называется случайная величина, которая принимает значения kxi с теми же вероятностями pi (i=1, 2, …, n).

m-й степенью случайной величины Х, то есть Хm, называется случайная величина, которая принимает значение  с теми же вероятностями pi (i=1, 2, …, n).

Суммой (разностью или произведением) случайных величин Х и Y называется случайная величина, которая принимает все возможные значения вида xi+yj (xi-yj или xi∙yj), где i=1, 2, …, n; j=1, 2, …, m, с вероятностями pij того, что случайная величина Х примет значение xi, а Y – значение yj: pij=Р[(X=xi) (Y=yj)].

Если случайные величины Х и Y независимы, то есть независимы любые события X=xi, Y=yj, то по теореме умножения вероятностей для независимых событий

pij=Р(X=xi)∙Р(Y=yj) = pi∙pj.