-
Зависимые и независимые случайные события.
События А, В называются зависимыми, если вероятность каждого из них зависит от того, произошло или нет другое событие.
Событие B называется независимым от события A, если его вероятность не меняется от того, произошло событие A или нет, т.е. выполняется условие:
Если событие B не зависит от A, то и событие A не зависит от B.
Доказательство.
Два события называются независимыми , если появление одного не меняет вероятность появления другого.
-
Теоремы умножения для независимых случайных событий.
Вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий.
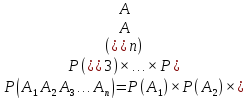
События называются независимыми в совокупности, если вероятность произведения всех событий равна произведению вероятностей всех событий
-
Теоремы умножения для зависимых случайных событий.
Вероятность умножения двух зависимых событий равна произведению вероятности появления одного события на условную вероятность другого события, найденную в предположении, что первое событие произошло.
Теорема справедлива для любого конечного числа событий
Док-во
-
Вероятность появления хотя бы одного события.
Доказательство.
Если событие
состоит
в появлении хотя бы одного из данных
событий
,
то противоположное событие
означает непоявление всех данных
событий, т.е. произведение событий
.
Вероятность суммы противоположных
событий равна 1.
P(
)
=
-
Формула полной вероятности. Формулы Бейеса.
Если событие A
может произойти только при условии
появления одного из событий (гипотез)
,
образующих полную группу, то вероятность
события A
равна сумме произведений вероятностей
каждого из этих событий (гипотез) на
соответствующие условные вероятности
события A.
Так как гипотезы
– единственно возможные, а событие A
по условию теоремы может произойти
только вместе с одной из гипотез, то
В
силу того что гипотезы
несовместны, можно применить теорему
сложения вероятностей:
По теореме умножения
:
)
=
Следствием формулы
полной вероятности является формула
Бейеса. Она применяется, когда событие
A,
которое может появиться только с одной
из гипотез
,
образующих полную группу событий,
произошло
и необходимо
найти условные вероятности гипотез
,
,…,
-
Повторение событий. Формула Бернулли.
Теорема. Если
вероятность p
наступления события A
в каждом испытании постоянна, то
вероятность
того, что событие A
наступит m
раз в n
независимых испытаниях, равна
,
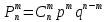где q
= 1 – p
Есть такие значения
m,
обладающие наибольшей вероятностью.
Число
наступления события A
в n
независимых испытаниях называется
наивероятнейшим, если вероятность
осуществления этого события
по крайней мере не меньше вероятностей
других событий
при
любом m.
,
p
,
,
