39. Понятие вариационного ряда

Определение:Вариационным рядом называется ряд вариант расположенных в порядке возрастания с соответственными частотами и относительными частотами.

Вариационный ряды бывают дискретные и интервальные.

Определение:Дискретным вариационным рядом называется ряд, который представляет собой выборку значений дискретной СВ.

Общий вид вариационного ряда:

Варианты:	x1	X2	…	xk
Частоты:	m1	M2	…	mk

Определение:Интервальным вариационным рядом называется ряд, который представляет собой выборку значений СВ.

Построенный интервал вариационного ряда можно разбить на полуинтервалы вида , т.е. произвести из группировку. Количество интервалов k рекомендовано выбирать по формуле

Стерджеса: . Длина каждого интервала .

Подсчитывая количество значений попавших в каждый полуинтервал получаем значение :

Варианты:			…
Частоты:	m1	m2	…	mk

Для наглядности представления дискретного и вариационного ряда используются графические представления:

1. Полигоны.

2. Гистограммы.

3. Камулянты.

40. Выборочные характеристики вариационного ряда.

Основной характеристикой вариационного ряда называется его среднее арифметическое или выборочное среднее: .

Для интервального ряда в качестве мы берём середину соответствия интервала.

Вариационный размах: .

Выборочная дисперсия: , , .

Выборочное среднее квадратичное отклонение: .

41. Точечные оценки. Метод максимального правдоподобия.

Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выбор­ки. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытовn.

Точечные оценки могут быть состоятельными, несмещенными и эффективными.

Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к ис­тинному значению числовой характеристики.

Несмещеннойна­зывается оценка, математическое ожидание которой равно оце­ниваемой числовой характеристике (параметру).

Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной счи­тают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины

Точечная оценка дисперсии, определяемая по формуле

Оценка сред­него квадратического отклонения

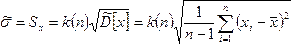
Метод максимального правдоподобия.

Пусть, как и прежде,  -- независимая выборка из распределения с функцией распределения , зависящей от неизвестного параметра Определим функцию правдоподобия, полагая

если  -- абсолютно непрерывна и имеет плотность , либо

если  есть функция распределения некоторой дискретной случайной величины , причем .

Переменные  следует считать основными для функции , а  -- дополнительными параметрами. Считая  фиксированными, найдем точку, в которой функция правдоподобия  принимает наибольшее значение. Понятно, что эта точка будет зависеть от заранее фиксированной выборки , следовательно, мы получим набор функций от выборки:

(36)

что и будет искомой оценкой по методу наибольшего правдоподобия.

Функция от выборки (36) называется оценкой наибольшего правдоподобия (о.н.п.), если