37. Уравнение прямой линии регрессии. Метод наименьших квадратов.

Теоретической линией регрессии называется линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи между признаками. Для взаимного погашения случайных причин линия регрессии проводится так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной (метод наименьших квадратов).

Рассмотрим уравнение прямой линии .

Для нахождения параметров и уравнения регрессии используем метод наименьших квадратов: сумма квадратов отклонений эмпирических точек от теоретической линии регрессии должна быть минимальной:

Параметр в линейном уравнении называют коэффициентом регрессии.

38. Выборочный метод

Вся подлежащая изучению совокупность объектов называется генеральной совокупностью. В математической статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данном реальном комплексе условий.

Та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности, назыв. выборочной совокупностью или выборкой.

Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности ( по выборке) выносит суждение о ее свойствах в целом.

Чтобы по данным выборке иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно.

Выборка назыв. репрезентативной (представительной), если она достаточно хорошо воспроизводит генеральною совокупность.

Виды выборок:

• Собственно-случайная выборка, образованная случайным выбором элементов без расчленения на части или группы;

• Механическая выборка, в которую элементы из генеральной совокупности отбираются через определенный интервал. Например, если объем выборки должен составлять 10%, то отбирается каждый 10-й элемент и т.д.;

• Типическая (стратифицированная) выборка, в которую случайным образом отбираются элементы из типических групп, на которые по некоторому признаку разбивается генеральная совокупность;

• Серийная (гнездовая) выборка, в которую случайным образом отбираются не элементы, а целые группы совокупности (серии), а сами серии подвергаются сплошному наблюдению.

ДВА способа образования выборки:

• Повторный отбор (по схеме возвращенного шара), когда каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран;

• Бесповторный отбор (по схеме невозвращенного шара), когда отобранный элемент не возвращается в общую совокупность.

Наименование характеристики	Генеральная совокупность	Выборка
Средняя
Дисперсия
Доля

- значение признака (случайной величины Х);

N и n - объемы генеральной и выборочной совокупностей;

и - число элементов генеральной и выборочной совокупностей со значением признака ;

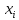M и m - число элементов генеральной и выборочной совокупностей, обладающих данным признаком.

Средние арифметические распределения признака в генеральной и выборочной совокупностях называются соответственно генеральной и выборочной средними, а дисперсии этих распределений – генеральной и выборочной дисперсиями. Отношение числа элементов генеральной и выборочной совокупностей, обладающих некоторым признаком А, к их объемам, называются соответственно генеральной и выборочной долями.

Важнейшей задачей выборочного метода является оценка параметров генеральной совокупности по данным выборки.