34. Математическое ожидание двумерной случайной величины. Свойства

Математическим ожиданием двумерной случайной величины называется совокупность двух математических ожиданий М[Х], М[Y],то есть упорядоченных пар М[Х], М[Y],которые определяются равенствами:

Если Х, У непрерывная случайная величина, то тогда

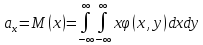
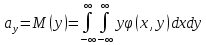
Свойства –точно такие же как и у мат ож случ величины, но эти свойства для функций

Свойство 1. Математическое ожидание постоянной равно самой этой постоянной.

М(С)=С×1=С

Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.

Ограничимся доказательством этого свойства только для суммы двух дискретных случайных величин, т.е. докажем, что

Под суммой двух дискретных сл. Величин понимается сл. Величина, которая принимает значения  с вероятностями

По определению

Но 

где  вероятность события  , вычисленная при условии, что  . В правой части последнего равенства перечислены все случаи появления события  , поэтому  равна полной вероятности появления события  , т.е.  . Аналогично  . Окончательно имеем

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

У			…
Q			…
Х			…
Р			…

35. Зависимые и независимые двумерные случайные величины

Случайные величины X и Y называются независимыми, если их совместная функция распределения F(x,y) представляется в виде произведения функций распределения (x) и 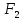(y) этих случайных величин, т.е.

.

В противном случае, при невыполнении равенства, случайные величины X и Y называются зависимыми.

т.е для независимых непрерывных случайных величин X и Y их совместная плотность равна произведению плотностей вероятности этих случайных величин .

Независимость случайных величин X и Y означает, что условные плотности вероятности каждой из них совпадают с соответствующими « безусловными» плотностями, т.е.

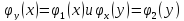
Зависимость между двумя случайными величинами называется вероятной (стохастической или статистической ) , если каждому значению одной из них соответствует определенное (условное) распределение другой .

Если случайные величины X и Y независимы, то линии регрессии X по Y и Y по X параллельны координатным осям Оx и Оy.

36. Ковариация и коэффициент корреляции.

Ковариация – математическое ожидание от произведения определения средних величин.

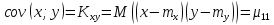
Для дискретной случайной величины:

Для непрерывных случайных величин:

Свойства ковариации:

1. Ковариация симметрична

2. Постоянный множитель можно выносить за знак ковариации k(cx, y) = k(x,cy) = ck(x,y)

3. Ковариация не изменится если к случайным величинам добавить случайные величины k(x+a, y) = k(x, y +b) = k(x+a, y+b) a,b R

4. Дисперсия случайной величины – это ковариация случайной величины с самой собой D(x) =

5. Дисперсия суммы = сумме дисперсий 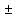удвоенная ковариация

D(x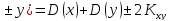

6.Если случайные величины независимы, то ковариация = 0

7. Ковариация по абсолютной величине не превосходит произведение средних квадратических отклонений.

||

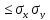
Коэффициент корреляции двух случайных величин – отношение их ковариации к произведению средних квадратических отклонений этих величин:

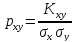
Свойства коэффициента корреляции:

1. 

2. Для независимых случайных величин (x, y – независимы) =0

3. Если x и y связаны линейной функциональной зависимостью

Y = ax + b, то если =1 (a>0) то это прямая линейная зависимость , если 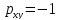то это обратная линейная зависимость (а0)

справедливо и обратное утверждение т.е. если модуль , то между величинами x, y существует линейная функциональная зависимость