Теория вероятностей (2 курс) экономический факультет

1. Основные правила комбинаторики. Перестановки. Размещения. Сочетания.

Комбинаторика – раздел математики, изучающий, в частности методы решения комбинационных задач – задач на подсчет числа различных комбинаций.

Правило суммы. Если множество A содержит n элементов, а множество B содержит m элементов, то элемент a или b можно выбрать n + m способами.

Правило произведения. Если множество A содержит n элементов, а множество B содержит m элементов, то элемент a и b можно выбрать n m способами.

Пусть дано множество, состоящее из n различных элементов. Из этого множества могут быть образованы комбинации (выборки) из m элементов (0 < m < n).

Перестановками Из N элементов называются комбинации (выборки), состоящие из N элементов и отличающиеся друг от друга только порядком следования элементов.

Размещениями из N элементов по M называются комбинации (выборки), состоящие из M элементов и отличающиеся друг от друга либо составом элементов, либо порядком их расположения (либо и тем и другим).

Сочетаниями Из N элементов по M называются комбинации (выборки), состоящие из M элементов, взятых из данных N элементов, и отличающиеся друг от друга только составом элементов.

Если в размещениях (сочетаниях) из n элементов по m некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения (сочетания) называют размещениями (сочетаниями) с повторениями из nэлементов по m.

Число размещений с повторениями из nэлементов по m:

Число сочетаний с повторениями из nэлементов по m:

2. Случайные события. Операции над случайными событиями.

Случайным событием ( или просто событием) в теории вероятности любой факт, который в результате испытания может произойти или не произойти. Событие – это не какое-нибудь происшествие, а лишь возможный исход, результат испытания.

Под испытанием (опытом, экспериментом) понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление.

Событие называется достоверным, если оно обязательно наступит в результате данного опыта, обозначается через Ω.

Событие называется невозможным, если оно заведомо не произойдет в результате проведения опыта. Обозначается Ø.

Если при каждом испытании, при котором происходит событие А, происходит и событие В, то говорят, что А влечёт за собой событие В (входит в В) или В включает событие А и обозначают А  В.

Два события называются несовместными, если появление одного из них появление другого события в одном и том же опыте, т.е. они не смогут произойти вместе в одном опыте. В противном случае события называются совместными.

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

Несколько событий образуют полную группу для данного события, если они являются попарно несовместными и во время испытания обязательно появится одно из этих событий.

Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие, т.е. все события имеют равные шансы.

Пространством элементарных исходов называется произвольное множество, элементам которого поставлены во взаимно однозначное соответствие элементарные исходы данного эксперимента.

1. Суммой событий А и В называется событие С = А + В, состоящее в

наступлении хотя бы одного из них (т.е. или А, или В, или А и В одновременно).

Суммой n событий является событие, заключающееся в появлении одного из событий , или их возможных комбинаций, или всех одновременно.

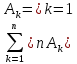
2. Произведением событий А и В называется событие С=А·В, состоящее в совместном наступлении этих событий (т.е. и А и В одновременно).

Произведением n событий является событие, заключающееся в появлении всех событий одновременно.

Дополнительным к событию A называется событие , означающее, что событие А не происходит.

Свойства операций над событиями:

1. А + В = В + А , А · В = В·А (переместительное); 2. (А + В)·С = А·С + В·С (распределительное); 3. (А + В) + С = А + (В + С) , (А·В)·С=А·(В·С) (сочетательное); 4. А + А = А , А·А = А; 5. А + Ω = Ω , А·Ω = А; 6. А + А = Ω , А· А = Ø. 7.   , , А  А ;