§3. Обход графов.

При решении многих практических задач, сформулированных в терминах графов (орграфов), необходим эффективный метод систематического обхода вершин (узлов) и ребер (дуг) графа.

Далее для представления вершин, смежных с вершиной , можно использовать список смежности 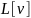, а для определения вершин, которые ранее посещались, — массив mark (метка), чьи элементы будут принимать только два значения: visited и unvisited.

Рассмотрим два метода обхода – поиск в глубину и поиск в ширину.

3.1. Поиск в глубину.

Этот метод обхода вершин графа называется поиском в глубину, поскольку поиск не посещенных вершин идет в направлении вперед (вглубь) до тех пор, пока это возможно.

Рекурсивный алгоритм поиска в глубину.

1. Поиск начинается с посещения некоторой фиксированной вершины-источника v.

2. Рассматривается произвольная вершина u, смежная с v. Она посещается.

3. Процесс повторяется с вершиной u в качестве источника.

Если на очередном шаге мы работаем с вершиной q и нет вершин, смежных с q и не рассмотренных ранее (новых), то возвращаемся из вершины q к вершине, которая была посещена до неё.

В том случае, когда это вершина v, процесс просмотра закончен.

Если некоторые вершины остались не посещенными, то выбирается одна из них в качестве источника и поиск повторяется.

Этот процесс продолжается до тех пор, пока обходом не будут охвачены все вершины орграфа .

Эскиз рекурсивной процедуры dfs (от depth-first search — поиск глубину), реализующей метод поиска в глубину, выглядит так

procedure dfs ( v: вершина );

var

w: вершина;

begin

(1) mark[v]:= visited;

(2) for каждая вершина w из списка L[v] do

(3) if mark[w] = unvisited then

(4) dfs(w)

end; { dfs }

Заметим, что процедура изменяет только значения массива mark.

Чтобы применить эту процедуру к графу, состоящему из n вершин, надо сначала присвоить всем элементам массива mark значение unvisited, затем начать поиск в глубину для каждой вершины, помеченной как unvisited. Описанное можно реализовать с помощью следующего кода:

for v:= 1 to n do

marklv]:= unvisited;

for v:= 1 to n do

if mark[v] = unvisited then

dfs (v)

Анализ рекурсивной процедуры поиска в глубину

Все вызовы процедуры dfs для полного обхода графа с 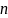вершинами и дугами, если 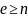, требуют общего времени порядка 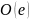. Чтобы показать это, заметим, что нет вершины, для которой процедура dfs вызывалась бы больше одного раза, поскольку рассматриваемая вершина помечается как visited в строке (1) еще до следующего вызова процедуры dfs и никогда не вызывается для вершин, помеченных этой меткой. Поэтому общее время выполнения строк (2) и (3) для просмотра всех списков смежности пропорционально сумме длин этих списков, т.е. имеет порядок . Таким образом, предполагая, что , общее время обхода по всем вершинам орграфа имеет порядок , необходимое для "просмотра" всех дуг графа.

Пример. Пусть процедура dfs применяется к ориентированному графу, представленному на рис. 1, начиная с узла А. Алгоритм помечает этот узел как visited и выбирает узел В из списка смежности узла А. Поскольку узел В помечен как unvisited, обход графа продолжается вызовом процедуры dfs(B). Теперь процедура помечает узел В как visited и выбирает первый узел из списка смежности узла В. В зависимости от порядка представления узлов в списке смежности, следующим рассматриваемым узлом может быть или С, или D.

Предположим, что в списке смежности узел С предшествует узлу D. Тогда осуществляется вызов dfs(C). В списке смежности узла С присутствует только узел А, но он уже посещался ранее. Поскольку все узлы в списке смежности узла С исчерпаны, то поиск возвращается в узел В, откуда процесс поиска продолжается вызовом процедуры dfs(D). Узлы A и С из списка смежности узла D уже посещались ранее, поэтому поиск возвращается сначала в узел В, а затем в узел А.

На этом первоначальный вызов dfs(A) завершен. Но орграф имеет узлы, которые еще не посещались: Е, F и G. Для продолжения обхода узлов графа выполняется вызов dfs(E).

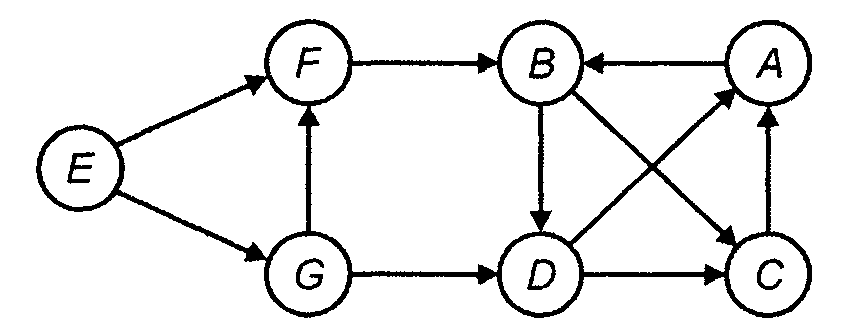
Рис. 1. Ориентированный граф

Нерекурсивный алгоритм поиска в глубину использует стек – особый вид списка, в котором добавление и извлечения элементов происходит только с одного конца, называемого вершиной стека.

1. Поиск начинается с посещения некоторой фиксированной вершины-источника v. Она помечается как visited (посещенная) и заносится в список обхода.

2. Все непосещенные вершины, смежные с v, помещаются в стек. (например, в порядке возрастания номеров), помечаются как visited.

3. Вершина из вершины стека заносится в список обхода, удаляется из стека, все ее непосещенные смежные вершины помещаются в стек в порядке возрастания номеров.

4. Шаг 3. повторяется, пока стек не опустеет.

В приведенном далее эскизе нерекурсивной процедуры dfs реализующей алгоритм поиска в ширину, посещенные вершины графа заносятся в стек 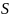. Также применяются заранее определенные функции работы со стеками:

TOP(S) – возвращает элемент из вершины стека.

PUSH(x, S) – помещает элемент x в вершину стека S.

POP(x, S) – удаляет элемент из вершины стека S.

EMPTY(S) – возвращает значение 1, если стек S пуст, и 0 в противном случае.

procedure dfs(v);

{dfs обходит в глубину все вершины, достижимые из вершины v}

var

S: STACK {стек для вершин}

x, y: вершина;

begin

mark[v]:=visited; writeln (v);

PUSH(v,S);

while not EMPTY(S) do begin

x:=TOP(S);

POP(S);

for для каждой вершины y, смежной с вершиной x do

if mark[y]=unvisited then begin

mark[y]:=visited; writeln(y);

PUSH(y,S);

end

end

end; {dfs}