§2.Представление графов.

Имеется два стандартных способа представления графа : как структуры списков смежности или как матрицы смежности. Оба способа представления применимы как для ориентированных, так и для неориентированных графов.

Рис. 1. Два представления неориентированного графа.

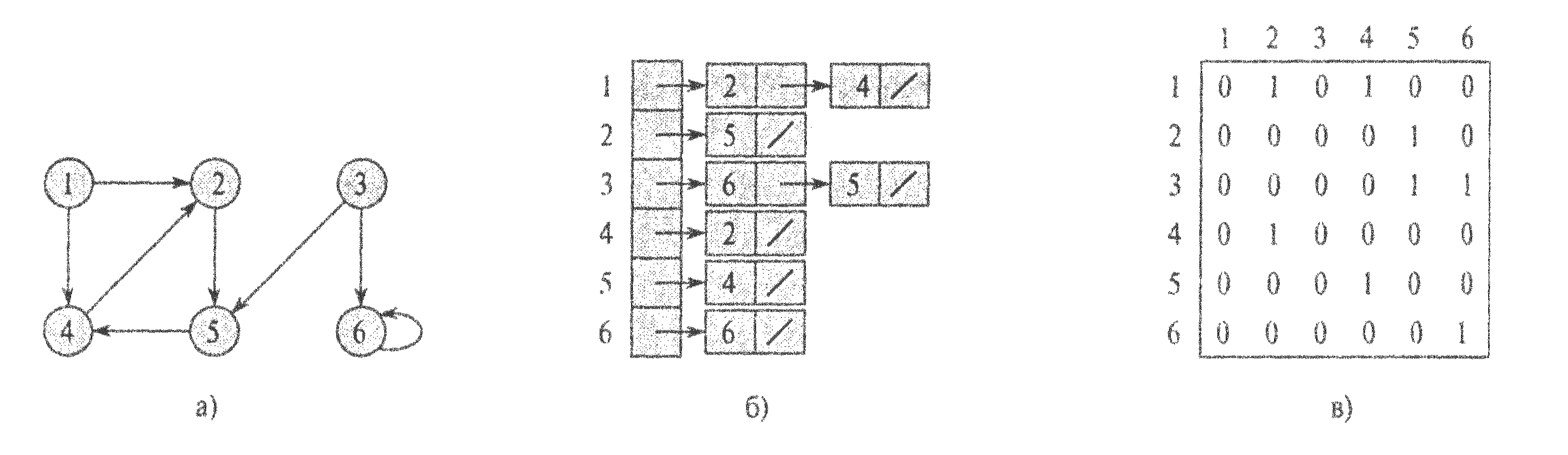
Рис. 2. Два представления ориентированного графа.

1. Структура списков смежности для графа состоит из 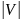списков смежности. Для каждой вершины 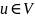её список смежности содержит все вершины , смежные с т.е. такие что .

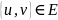Представление орграфа реализуется аналогично.

Вершины в каждом списке обычно хранятся в произвольном порядке. На рис. 1.б. показано такое представление графа, изображенного на рис. 1.а. Аналогично, на рис. 2.б. показана структура списков смежности ориентированного графа, изображенного на рис. 2.а.

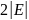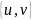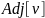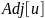Если — неориентированный граф, то сумма длин всех списков смежности равна , поскольку ребро , будучи неориентированным, появляется в списке как , и в списке — как .

Если — ориентированный граф, то сумма длин всех списков смежности равна 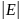, поскольку дуге 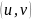однозначно соответствует элемент в списке .

Списки смежности легко адаптируются для представления взвешенных графов, то есть графов, с каждым ребром которых связан определенный вес(метка), обычно определяемый весовой функцией . Например, пусть — взвешенный граф с весовой функцией 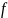. Вес 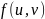ребра 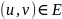хранится вместе с вершиной в каждом элементе списка смежности . Представление с помощью структуры списков смежности достаточно гибко в том смысле, что легко адаптируется для поддержки многих других вариантов графов.

Недостатки представления при помощи структуры списков смежности:

1. Проверка наличия ребра (дуги ) занимает время O(n), где n – кол-во узлов, так как требуется поиск в списке , а он в худшем случае имеет длину n.

2. Добавление и удаление вершины (узла) требует изменения структуры данных.

Преимущества представления при помощи структуры списков смежности::

1. В случае неупорядоченных списков добавление дуги производится за время O(1) = const(n);

2. Хранение структуры требует объема памяти O(n) +О(k), n – кол-во узлов, k – кол-во дуг. Здесь O(n) – объем памяти для хранения массива указателей на начала списков, O(k) – для хранения элементов списков, содержащих в сумме k элементов

2. Матрицей смежности графа называется матрица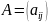 размера 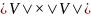, такая что

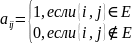
На рис. 1.в и 2.в показаны представления с использованием матрицы смежности неориентированного и ориентированного графов, показанных на рис. 1.а и 2.а соответственно. Матрица смежности графа требует объем памяти, равный 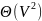, независимо от количества ребер графа.

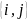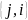Отметим симметричность матрицы смежности на рис. 1.в относительно главной диагонали. Поскольку граф неориентирован, и представляют одно и то же ребро, то в матрице смежности 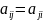. В ряде приложений это свойство позволяет хранить только элементы матрицы, находящиеся на главной диагонали и выше нее, что позволяет почти в два раза сократить необходимое количество памяти.

3. Матрицей весов рёбер взвешенного графа с весовой функцией называется матрица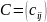 размера , такая что

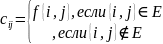
Недостатки представления при помощи матриц смежности и весов рёбер:

1. Добавление и удаление вершины (узла) требует изменения структуры данных.

2. Хранение матрицы требует объема памяти O(n²).

Преимущества представления при помощи матрицы смежности:

1. Проверка наличия ребра (дуги ) занимает время O(1) = const(n) , поскольку для этого требуется лишь доступ к элементу матрицы .

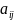2. Добавление и удаление ребра (дуги) за время O(1) = const(n);

Обычно более предпочтительно представление с помощью структуры списков смежности, поскольку оно обеспечивает компактное представление разреженных графов, то есть таких, для которых гораздо меньше .

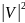Представление при помощи матрицы смежности предпочтительнее в случае плотных графов, то есть когда значение близко к , или когда нужно иметь возможность быстро определить, имеется ли ребро, соединяющие две данные вершины.