
- •§12 Алгоритмы поиска элементов во множестве.
- •1. Последовательный поиск
- •2. Бинарный поиск
- •3. Деревья бинарного поиска
- •§13 Абстрактные типы данных. Методы представления множеств.
- •1. Реализация атд «множество» посредством двоичных векторов
- •2. Реализация атд «множество» с помощью массивов
- •3. Реализация атд «множество» посредством связанных списков
- •§14. Реализация атд «Словарь». Хеширование.
- •1. Открытое хеширование
- •2. Закрытое хеширование.
- •2.2. «Случайные» методики повторного хеширования
§12 Алгоритмы поиска элементов во множестве.
Рассмотрим
задачу поиска в конечном множестве
 ,
называемом таблицей элементов, элемента,
удовлетворяющего некоторому условию.
,
называемом таблицей элементов, элемента,
удовлетворяющего некоторому условию.
Пусть
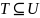 ,
,
 -некоторое
универсальное множество с заданным на
нем линейным
порядком
т.е. отношением «< », которое:
-некоторое
универсальное множество с заданным на
нем линейным
порядком
т.е. отношением «< », которое:
Антисимметрично:
 из
из
 и
и

Транзитивно: из и
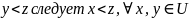
Связано:
 или
или
 или
или
 .
.
1. Последовательный поиск
Линейный, последовательный поиск — алгоритм нахождения заданного элемента z поочередным сравнением с элементами таблицы в том порядке, в котором они расположены.
Данный алгоритм является простейшим алгоритмом поиска, не накладывает никаких ограничений на таблицу и имеет простейшую реализацию.
В худшем случае потребуется просмотр всей таблицы для отыскания элемента z или установления, что z в таблице отсутствует. Таким образом, эффективность линейного поиска равна O(n), где n=|T|. Это является основным недостатком алгоритма. В связи с малой эффективностью по сравнению с другими алгоритмами поиска линейный поиск обычно используют только если таблица содержит мало элементов. Тем не менее, преимуществом линейного поиска является то, что он не требует дополнительной памяти или обработки/анализа таблицы, так что может работать в потоковом режиме при непосредственном получении данных из любого источника.
Далее приведена процедура, реализующая линейный поиск элемента z в таблице (одномерном массиве) Т. Переменные L и R содержат, соответственно, левую и правую границы отрезка массива, где ищется нужный элемент. Исследования начинаются с первого элемента отрезка. Если этот элемент не совпадает с искомым z, осуществляется переход к следующему элементу. Таким образом, в результате каждой проверки область поиска уменьшается на один элемент.
begin
T[R+1]:=z;
x:= L;
(3)while T[x] <> z do x := x + 1;
(4) if x < R+1 then return x; // элемент найден в позиции x
(5) else return -1; // элемент не найден
end;
Использован цикл while, т.к. в цикле со счетчиком по x при каждом прохождении тела цикла требуется проверка условия окончания цикла x=R.
Для гарантированного выхода из цикла на R+1 – ом шаге в таблицу добавлен элемент T[R+1]:=z.
2. Бинарный поиск
Бинарный поиск возможен, когда элементы в таблице упорядочены и ячейки таблицы распределены последовательно в памяти с произвольным доступом.
Поиск
элемента
 в отрезке
в отрезке
 :
:
-
Новый индекс
 для «средней точки» устанавливается в
середине отрезка
(это
дает самый эффективный алгоритм).
для «средней точки» устанавливается в
середине отрезка
(это
дает самый эффективный алгоритм).
-
Если
 ,
то поиск продолжается на отрезке [b,
c-1];
,
то поиск продолжается на отрезке [b,
c-1];
-
Если
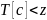 ,
то далее ищем в отрезке [c+1,
e];
,
то далее ищем в отрезке [c+1,
e];
-
Если
 ,
то искомый элемент найден и поиск
завершен.
,
то искомый элемент найден и поиск
завершен.
begin
(1) b:=1;
(2) e:=n;
(3) while b<=e do begin
(4) c:=(b+e) div 2;
(5) if T[c]>z then e:=c-1;
(6) else if T[c]<z then b:=c+1;
(7) else return c;
end;
(8) return «не найдено»;
end
Рассмотрим сложность алгоритма бинарного поиска.
Тело цикла (4)-(7) требует времени О(1).
Оценим
количество итераций цикла (3)-(7),
предполагая, что длина отрезка является
степенью двойки:
 .
(В остальных случаях сложность алгоритма
можно оценить исходя из Замечания 1 §
6)
.
(В остальных случаях сложность алгоритма
можно оценить исходя из Замечания 1 §
6)
-После
первой итерации длина рассматриваемого
отрезка равна
 .
.
-После
второй итерации -
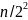 .
.
……………………………………
-После
k-й
итерации -
 .
Это означает, что b=e.
Далее, в строке (4) получим с=b=e,
и если искомый элемент всё же не будет
найден (строка (7)), то операции в строке
(5) или (6) приведут к условию b>e,
и цикл закончит работу.
.
Это означает, что b=e.
Далее, в строке (4) получим с=b=e,
и если искомый элемент всё же не будет
найден (строка (7)), то операции в строке
(5) или (6) приведут к условию b>e,
и цикл закончит работу.
Таким
образом, количество итераций цикла
(3)-(7) равно
 .
.
Время выполнения цикла (3)-(7) равно
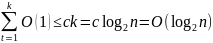
Таким
образом сложность алгоритма равна
 .
.
