
- •Глава 1. Основы анализа алгоритмов §1. Интуитивное понятие алгоритма и его уточнение
- •§2. Меры сложности алгоритмов
- •§3. Асимптотический анализ оценки сложности алгоритмов
- •§4. Свойства асимптотических оценок функций.
- •Если и , то , т. Е.
- •§5. Практический анализ эффективности программ.
- •§6. Анализ рекурсивных программ. Рекуррентные отношения.
- •§7. Стратегия декомпозиции. Анализ сложности алгоритмов декомпозиции.
- •I. Мультипликативные управляющие функции
- •II. Другие управляющие функции.
§6. Анализ рекурсивных программ. Рекуррентные отношения.
Рекурсивной процедурой называется процедура, прямо или косвенно обращающаяся к себе.
Глубиной рекурсии называется количество рекурсивных обращений, требуемых для вычисления рекурсивной функции.
Пример 1
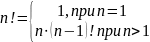 -
рекурсивная функция. Требует
последовательных обращений к самой
себе, то есть вычисления
-
рекурсивная функция. Требует
последовательных обращений к самой
себе, то есть вычисления
 ,
,
 ,
…, 2!, 1!. Глубина рекурсии при вычислении
равна
.
Алгоритм и анализ его сложности - см.
практические занятия.
,
…, 2!, 1!. Глубина рекурсии при вычислении
равна
.
Алгоритм и анализ его сложности - см.
практические занятия.
Анализ рекурсивных программ сложен и, как правило, требует решения дифференциальных уравнений. Рассмотрим наиболее простые случаи.
Пример 2. Рассмотрим процедуру-функцию сортировки слиянием mergesort(L):
Вход: список L длины n.
Выход: список L отсортированный по убыванию.
Функция mergesort использует процедуру merge(L1,L2), которая просматривает два отсортированных по убыванию списка L1 и L2. Сравнивая наибольшие элементы из L1 и L2 она выбирает наибольший из 2-х, удаляет его из L1 (или L2) и помещает в выходные данные. Затем снова сравнивает наибольшие элементы из оставшихся в L1 и L2 и т. д. Выход процедуры merge(L1,L2) – один отсортированный по убыванию список, содержащий все элементы L1 и L2.
Известно,
что на списках L1
и L2
длиной
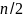 процедура merge
выполняется за время равное
процедура merge
выполняется за время равное
 .
.
function mergesort(L : list, n : integer) : list
{L – список типа list длиной n, n – степень числа 2}
var L1, L2 : list;
begin
(1) if n =1 then return(L)
else
begin
(2) {разбиение L на две части L1 и L2, каждая длиной n/2}
(3) return(merge(mergesort(L1, n/2), mergesort(L2, n/2));
end;
end.
Пусть - время выполнения megesort(L, n).
При
 в строке (1) действие return(L)
имеет временную сложность
в строке (1) действие return(L)
имеет временную сложность
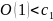 ,
где
,
где
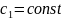 .
.
При
строка
(3)
: mergesort(L1,
n/2)
– временная сложность

mergesort(L2, n/2) – временная сложность
merge(mergesort(L1, n/2), mergesort(L2, n/2)) – временная сложность
строка (2) : время на разбиение L на две части – считаем
Итого
в (2)-(3):
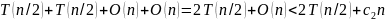 ,
для некоторого
,
для некоторого
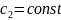 .
.
Таким образом, для всей программы
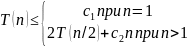 (1)
(1)
Замечание 1.
Процедуру
merge
и оператор (2) можно модифицировать для
работы не только в случае
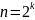 для некоторого
для некоторого
 .
.
В
других случаях , когда
 ,
практически для всех алгоритмов можно
предполагать, что
,
практически для всех алгоритмов можно
предполагать, что

Определение 1. Рекуррентным соотношением (рекуррентной формулой) называется соотношение вида
 (2)
(2)
позволяющее
вычислять n-й
член последовательности
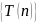 ,
если известны предыдущие k
членов.
,
если известны предыдущие k
членов.
Множество всех последовательностей вида , удовлетворяющих данному рекуррентному соотношению, называется общим решением рекуррентного соотношения.
Методы решения рекуррентных соотношений – см. курс дискретной математики.
Рассмотрим
один из способов решения – метод
подстановок.
В правую часть (2) последовательно
подставляются выражения для
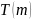 ,
,
 ,
чтобы исключить из правой части (2) все
выражения
для
,
чтобы исключить из правой части (2) все
выражения
для
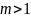 ,
оставляя только 𝑇
,
оставляя только 𝑇 .
Такая формула называется замкнутой
формулой
для
.
.
Такая формула называется замкнутой
формулой
для
.
Недостатком метода является то, что приходится находить возникающие при преобразованиях суммы различных последовательностей, что бывает трудоемко сделать точно. В таком случае обычно находятся верхние границы этих сумм.
Пример 3.
Оценим решение рекуррентного соотношения (1) из примера 2.
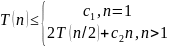 (1)
(1)
Будем
рассматривать 2 строку оценки (1). Подставим
в нее
вместо
:
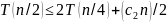 .
.
Подставим полученную оценку для во вторую строку (1):
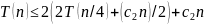 ,
то есть
,
то есть
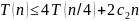 (2)
(2)
Подставим
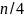 вместо
во вторую строку (1)
вместо
во вторую строку (1)

Подставим
полученную оценку для
 в (2)
в (2)
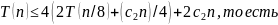
 (3)
(3)
Из (1), (2), (3) с помощью метода математической индукции можно получить общую формулу
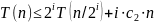 (4)
(4)
Предположим,
что
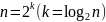 .
При
.
При
 из (4) следует
из (4) следует
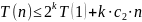 .
.
Так
как
 (см. пример 2 при n=1),
то
(см. пример 2 при n=1),
то
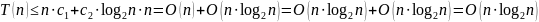
Таким
образом, функция mergesort
имеет эффективность
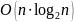 .
.
