
- •Глава 1. Основы анализа алгоритмов §1. Интуитивное понятие алгоритма и его уточнение
- •§2. Меры сложности алгоритмов
- •§3. Асимптотический анализ оценки сложности алгоритмов
- •§4. Свойства асимптотических оценок функций.
- •Если и , то , т. Е.
- •§5. Практический анализ эффективности программ.
- •§6. Анализ рекурсивных программ. Рекуррентные отношения.
- •§7. Стратегия декомпозиции. Анализ сложности алгоритмов декомпозиции.
- •I. Мультипликативные управляющие функции
- •II. Другие управляющие функции.
§4. Свойства асимптотических оценок функций.
Теорема 1.
Если и , то , т. Е.
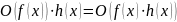
Если , то
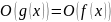 ,
т. е.
,
т. е.
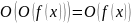

Если , то
 ,
т. е.
,
т. е.
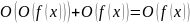
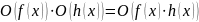 – правило
произведений.
– правило
произведений.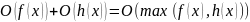 –правило
сумм,
где под функцией
–правило
сумм,
где под функцией
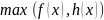 понимается функция
понимается функция
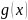 такая, что
такая, что
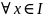
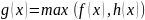 =
=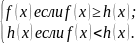
Доказательство
Т. к. , то
 .
.
Т.
к.
,
то
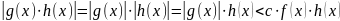
 по определению 1 §3
.
по определению 1 §3
.
Пусть
 причем по определению 1 §3
причем по определению 1 §3
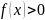 .
Пусть
.
Пусть
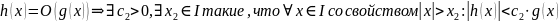 ,
причем
,
причем
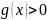 .
.
Обозначим
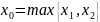 .
Тогда
.
Тогда
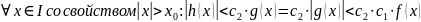 .
.
Таким
образом
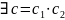 ,
,
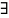
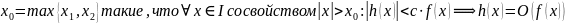 т. е.
и, таким образом,
.
т. е.
и, таким образом,
.
Пусть ,
 .
Тогда
.
Тогда
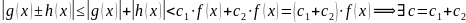 ,
,
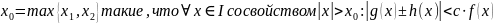 причем по определению 1 §3
причем по определению 1 §3
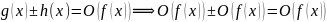
Пусть ,
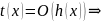
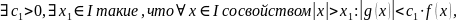
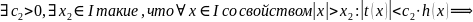 ,
,

Пусть ,

Тогда
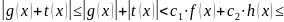
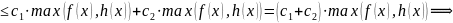
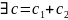 ,
,
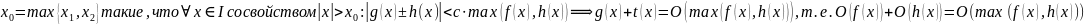 .
Теорема доказана.
.
Теорема доказана.
Замечание 1. Правило сумм (Теорема 1 (6)) используется для вычисления времени выполнения последовательных фрагментов программ.
Пусть
два программных фрагмента
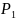 и
и
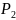 выполняются соответственно за время
выполняются соответственно за время
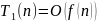 и
и
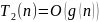 .
Время их последовательного выполнения
.
Время их последовательного выполнения
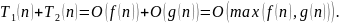
Лемма
1.
Если существует конечный предел
 =k,
то
=k,
то
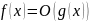 при
.
при
.
Используя определение 1 §3 или лемму 1 можно доказать следующую теорему.
Теорема 2.
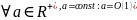 .
.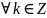
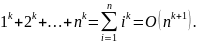
Пусть
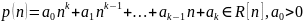 .
Тогда
.
Тогда


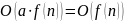 .
.
§5. Практический анализ эффективности программ.
Приведем общие правила анализа программ без определения констант пропорциональности:
Время выполнения операторов присваивания обычно имеет порядок
 .
.
Исключение составляют языки программирования, где можно присваивать большие массивы, вызывать функции в операторах присваивания.
Временная сложность программных фрагментов, выполняемых последовательно, оценивается а) при фиксированном количестве фрагментов с помощью правила сумм (см.Т.1§4):
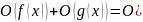 б)
при количестве программных фрагментов,
зависящем от n
(в т.ч. в цикле, где число итераций зависит
от n),
применяется свойство:
б)
при количестве программных фрагментов,
зависящем от n
(в т.ч. в цикле, где число итераций зависит
от n),
применяется свойство:
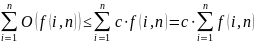 (1)
(1)Время выполнения условных операторов if-then-else состоит из
а) времени вычисления логического выражения, стоящего после if (обычно это время ).
б) наибольшего из времен выполнения операторов групп then и else.
Время выполнения цикла – сумма времени выполнения всех итераций цикла, включая проверку условия прекращения (обычно ).
Для программ, содержащих несколько процедур, среди которых нет рекурсивных:
а) определить время выполнения процедуры , не имеющей вызовов других процедур (такая существует, например, это самая внутренняя из вложенных процедур);
б) определить время выполнения процедур, вызывающих эту процедуру и т. д.
в) определить время выполнения всех процедур найти время выполнения всей программы.
Пример 1. Проанализируем программу сортировки методом «пузырька». Массив А упорядочивается по возрастанию.
procedure bubble(var A: array[1..n] of integer)
var
i, j, temp : integer;
begin
(1) for i := 1 to n-1 do
(2) for j := n downto i + 1 do
(3) if A[j -1] > A[j] then
begin
{Переставляем местами A[j -1] и A[j ]}
(4) temp := A[j-1];
(5) A[j-1] := A[j];
(6) A[j] := Temp ;
end;
end
Пусть n – объем вводимых данных, т. е. количество элементов, подлежащих сортировке.
Проанализируем время выполнения программы, переходя от внутренних операторов к внешним.
Группа
операторов присваивания (4)-(6) выполняется
за время
каждый (см. п.1). Вся последовательность
(4)-(6)
по правилу п.2 за время
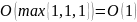 .
.
Для оператора if в строке (3) вычисление логического условия A[j -1] > A[j] требует времени (см. п. 3).
Наибольшее время выполнения имеет группа операторов then (4)-(6) - как показано выше, . Таким образом, время выполнения группы (3) – (6) требует времени .
Цикл
(2)-(6) выполняется n-i
раз, причем на каждом проходе группа
операторов тела цикла (3)-(6) требует
времени
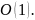
Итого,
применяя свойство (1), получим
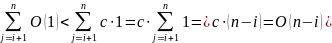 .
.
Цикл
(1)-(6) выполняется n-1
раз при i
от 1 до n-1,
каждый раз тело цикла требует времени
 ,
таким образом, весь цикл, согласно
свойству (1), выполнится за время
,
таким образом, весь цикл, согласно
свойству (1), выполнится за время
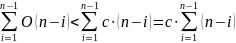 Полученная
сумма является арифметической прогрессией,
члены которой
Полученная
сумма является арифметической прогрессией,
члены которой
 ,
,
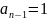 ,
тогда сумма первых
,
тогда сумма первых
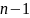 членов будет равна
членов будет равна
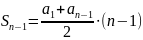 ,
то есть искомое время
,
то есть искомое время
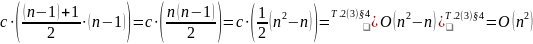
Согласно правилам пп. 1-5 найдена эффективность, то есть асимптотическая временная сложность алгоритма в худшем случае.
