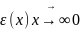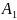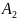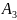- •Глава 1. Основы анализа алгоритмов §1. Интуитивное понятие алгоритма и его уточнение
- •§2. Меры сложности алгоритмов
- •§3. Асимптотический анализ оценки сложности алгоритмов
- •§4. Свойства асимптотических оценок функций.
- •Если и , то , т. Е.
- •§5. Практический анализ эффективности программ.
- •§6. Анализ рекурсивных программ. Рекуррентные отношения.
- •§7. Стратегия декомпозиции. Анализ сложности алгоритмов декомпозиции.
- •I. Мультипликативные управляющие функции
- •II. Другие управляющие функции.
§3. Асимптотический анализ оценки сложности алгоритмов
Для
заданного алгоритма
точное определение величины
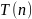 может быть сложно или вообще невозможно,
так как:
может быть сложно или вообще невозможно,
так как:
Количество операторов, выполняемых алгоритмом при решении данной задачи различно в зависимости от того, какая алгоритмическая модель применяется при реализации алгоритма.
Операторы неравносильны друг другу по времени их выполнения, затрачиваемым объемам памяти и т.д., что зависит так же от особенностей конкретной машины.
Поэтому в качестве основной меры эффективности алгоритма принимается асимптотическая временная сложность в худшем случае.
Определение.1
Пусть
 и
и
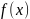 – функции, определенные на некотором
бесконечном множестве
– функции, определенные на некотором
бесконечном множестве
 значений аргумента
,
значений аргумента
,
 .
.
Говорят,
что
имеет верхний порядок роста
 при
при
 и
записывают
и
записывают
 ,
если
,
если
 .
.
Требования
определения 1 означают, что начиная с
некоторого, достаточно большого по
модулю
 выполняется
выполняется
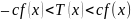 ,
т.е. график функции
лежит между графиками
,
т.е. график функции
лежит между графиками
 и
и .
.
По
определению 1 запись
 может означать любую функцию
может означать любую функцию
 ,
удовлетворяющую условиям определения
1.
,
удовлетворяющую условиям определения
1.
Определение.2
Говорят,
что алгоритм имеет эффективность
(т.е. асимптотическую временную сложность
в худшем случае)
 или порядка
или порядка
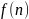 ,
если для него
,
если для него
 .
.
Пример
1.
Предположим,
известна точно временная сложность
 .
Покажем, что
.
Покажем, что
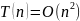 .
Согласно определению 1, выбирая
.
Согласно определению 1, выбирая
 и
и ,
получаем
,
получаем
 .
.
Неравенство
верно т.к., например,
 – убывающая функция натурального
аргумента
– убывающая функция натурального
аргумента
 и имеет наибольшее значение при
и имеет наибольшее значение при
 .
.
Таким
образом,
 .
.
Согласно
определению 2, говоря об эффективности
алгоритма, достаточно указать лишь
верхний порядок роста его функции
его функции
 .
При этом игнорируется мультипликативная
константа
.
При этом игнорируется мультипликативная
константа
 ,
из неравенства
,
из неравенства
 в определении 1. То есть, например, с
точки зрения определения 2 алгоритмы,
для которых
в определении 1. То есть, например, с
точки зрения определения 2 алгоритмы,
для которых
 и
и
 имеют одинаковую эффективность
имеют одинаковую эффективность
 .
.
Это оправдано, так как функция большей степени, чем константа , определяет относительное увеличение размера задачи, решаемой данным алгоритмом при увеличении ресурса времени. (см. далее пример 2 и замечание 1).
Однако, при сравнении времени работы различных алгоритмов над задачами небольшого размера n константы могут играть важную роль (см. пример 3).
Пример
2.
Предположим, известны точно временные
сложности
 алгоритмов
алгоритмов
 ,
решающих некоторую задачу.
,
решающих некоторую задачу.
В
таблице показан максимальный размер
задачи
 ,
решаемой алгоритмом
,
решаемой алгоритмом
 за время
за время
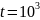 .
При этом
находится из условия
.
При этом
находится из условия
 .
.
Например,
 .
.
Аналогично
находится максимальный размер задачи
 решаемой за время
решаемой за время
 из условия
из условия
 .
.
Например
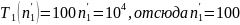 .
.
Таким
образом, за счет десятикратного увеличения
времени работы (или 10-кратного повышения
быстродействия компьютера) при
использовании алгоритма
максимальный размер решаемой задачи
увеличивается в
 раз.
раз.
Например,
для алгоритма
 раз.
раз.
Алгоритм
|
Временная сложность |
Эффективность
|
max объём задачи решаемой за |
max объём задачи решаемой за |
Увеличение max объема |
|
|
|
10 |
100 |
10.0 |
|
|
|
14 |
45 |
3.2 |
|
|
|
12 |
27 |
2.3 |
|
|
|
10 |
13 |
1.3 |
Из таблицы очевидно преимущество алгоритмов с эффективностью . Тогда как для алгоритмов с эффективностью , 10-кратное повышение быстродействия компьютера дает увеличение размера решаемой задачи всего в 1.3 раза.
На
практике, независимо от быстродействия
компьютера, алгоритм с экспоненциальной
эффективностью
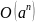 ,
,
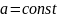 может решать лишь очень небольшие
задачи.
может решать лишь очень небольшие
задачи.
Замечание
1.
Легко показать, что если в расчетах
примера 2, функцию
заменить на
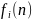 ,
т.е. вместо
использовать
,
вместо
использует
,
т.е. вместо
использовать
,
вместо
использует
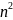 и т.д., то результаты последнего столбца
не изменятся (с точностью до ошибки
округления).
и т.д., то результаты последнего столбца
не изменятся (с точностью до ошибки
округления).
В общем случае, можно показать, что мультипликативные константы функции и константы из определения 1 не влияют на относительное увеличение максимального объема задачи при увеличении быстродействия компьютера.
П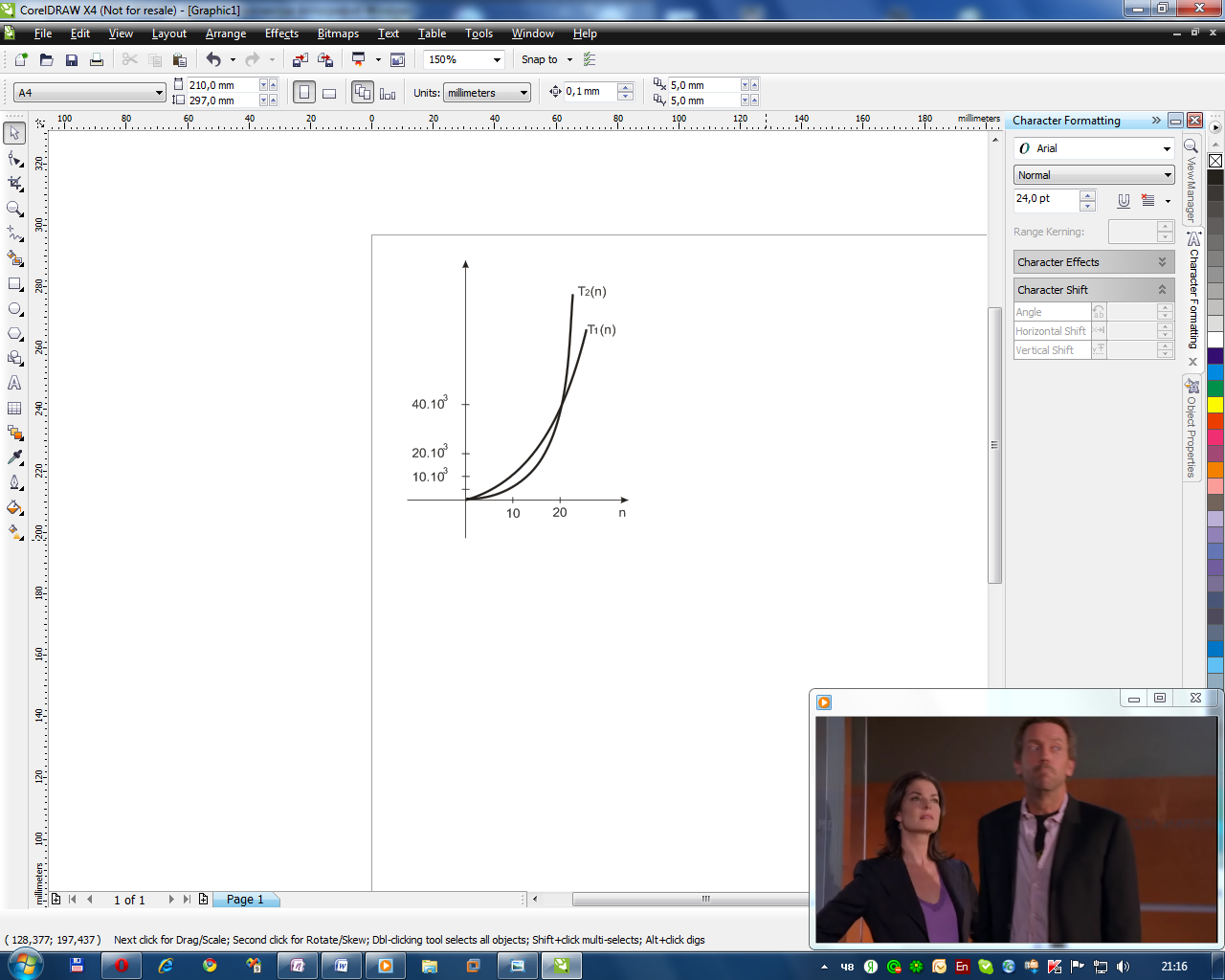 ример
3.
Рассмотрим два алгоритма
и
временные сложности, которых соответственно
ример
3.
Рассмотрим два алгоритма
и
временные сложности, которых соответственно
 и
и
 .
.

При
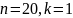 ,
т.е.
,
т.е.

При
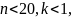 т.е.
т.е.
При
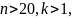 т.е
т.е
Очевидно,
что величина 20 зависит от мультипликативных
констант в функциях
 .
.
При
 алгоритм
с эффективностью
работает дольше, чем
с эффективностью
.
алгоритм
с эффективностью
работает дольше, чем
с эффективностью
.
При
 работает дольше, чем
.
работает дольше, чем
.
Таким образом, если программы выполняются преимущественно с входными данными небольшого размера, алгоритм лучше.
Тем
не менее, если речь идет об асимптотической
временной сложности, т.е. об эффективности
алгоритма при
 ,
то
с эффективностью
работает быстрее, чем
с эффективностью
при достаточно больших
.
На этот факт не влияют мультипликативные
константы в
,
то
с эффективностью
работает быстрее, чем
с эффективностью
при достаточно больших
.
На этот факт не влияют мультипликативные
константы в
 и
и
 .
.
Наряду
с оценкой верхнего порядка роста функции
,т.е.
указанием
,
так что
 ,
рассматривается также понятия нижнего
порядка роста функции
.
,
рассматривается также понятия нижнего
порядка роста функции
.
Определение
3.
Пусть
и
– функции, определенные на некотором
бесконечном множестве
значений аргумента
 .
Говорят, что
имеет нижний порядок роста
при
и
записывают
.
Говорят, что
имеет нижний порядок роста
при
и
записывают
 ,
если
,
если
 .
.
Для
асимптотического анализа функций, т.е.
анализа их поведения при стремлении
аргумента к
 ,
полезно следующее понятие.
,
полезно следующее понятие.
Определение.4
Пусть
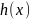 и
– функции, определенные на некотором
бесконечном множестве
значений аргумента
,
и
и
– функции, определенные на некотором
бесконечном множестве
значений аргумента
,
и
 .
Говорят, что
.
Говорят, что
 ,
если
,
если

Иначе
говорят,
 ,
где
,
где
 или
или
 ,
где
,
где