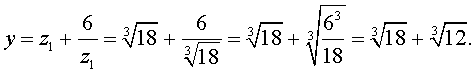http://www.dpva.info/Guide/GuideMathematics/Equations

Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.

Квадратным уравнением называется уравнение вида

                  ,

Где x - переменная, a, b, c - постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта: 

Формула дискриминанта:

.

О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

• D>0 - уравнение имеет 2 различных вещественных корня

• D=0 - уравнение имеет 2 совпадающих вещественных корня

• D<0 - уравнение имеет 2 мнимых корня (для непродвинутых пользователей - корней не имеет)

В общем случае корни уравнения равны:

.

Очевидно, в случае с нулевым дискриминантом, оба корня равны

.

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

В таком случае корни уравнения вычисляются по формуле:

 

Теорема Виета.

Приведенным квадратным уравнением называется уравнение вида   ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене,

то есть при х².

Квадратное уравнение имеет вид:

Стандартный метод нахождения корней уравнения происходит в два этапа. Сначала вычисляется дискриминант уравнения по формуле

Затем считаются корни по формуле

Данный онлайн калькулятор решает квадратные уравнения именно таким способом.

**********

Если известны корни уравнения, то исходный многочлен можно разложить на множители:

В ряде задач удобно использовать теорему Виета, которая выглядит следующим образом:

********************************************************************

Как решать квадратные уравнения? Дискриминант. http://www.egesdam.ru/page221.html

Поработаем с квадратными уравнениями. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:

Например:

Здесь  а =1; b = 3; c = -4

Или:

Здесь  а =2; b = -0,5; c = 2,2

Или:

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза  «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения  а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Вот и всё.

Какие случаи возможны при использовании этой формулы? Всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же… Самые распространённые ошибки – путаница со знаками  значений  a, b и с.  Вернее, не с их знаками (где там путаться?),  а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Итак, как решать  квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:

Или так:

Это неполные квадратные уравнения. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с.

Сообразили? В первом примере  a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут! Не получается? То-то… Следовательно, можно уверенно записать: х = 0, или х = 4

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х = +3 и х = -3.

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня. Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.…  За которые потом бывает больно и обидно…

Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает? Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось - надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом,  равен -1. Значит, всё верно! Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий. Если в вашем уравнении есть дробные коэффициенты,  -  избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Справочник по математике

Алгебра

Кубические уравнения

Решение кубических уравнений. Формула Кардано

Схема метода Кардано

      Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)

(1)

где   -  произвольные вещественные числа,

      Вывод формулы Кардано состоит из двух этапов.

      На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.

      На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.

Приведение кубических уравнений к трехчленному виду

      Разделим уравнение (1) на старший коэффициент . Тогда оно примет вид

(2)

где -  произвольные вещественные числа.

      Заменим в уравнении (2) переменную   на новую переменную  по формуле:

(3)

      Тогда, поскольку

то уравнение (2) примет вид

(4)

      Если ввести обозначения

то уравнение (4) примет вид

(5)

где -  вещественные числа.

      Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.

      Первый этап вывода формулы Кардано  завершён.

Сведение трёхчленных кубических уравнений к квадратным уравнениям

      Будем искать решение уравнения (5) в виде

(6)

где  -  новая переменная.

      Поскольку

то выполнено равенство:

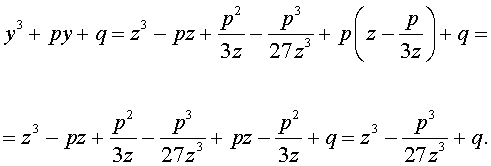
      Следовательно, уравнение (5) переписывается в виде

(7)

      Если теперь уравнение (7) умножить на , то мы получим квадратное уравнение относительно :

(8)

Формула Кардано

      Решение уравнения (8) имеет вид:

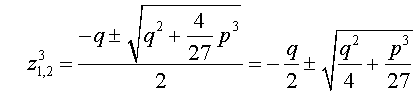
      Следовательно,

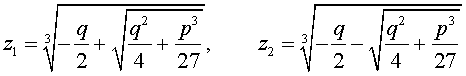
      В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:

(9)

      В развернутой форме эти решения записываются так:

	(10)
	(11)

      Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.

      Действительно,

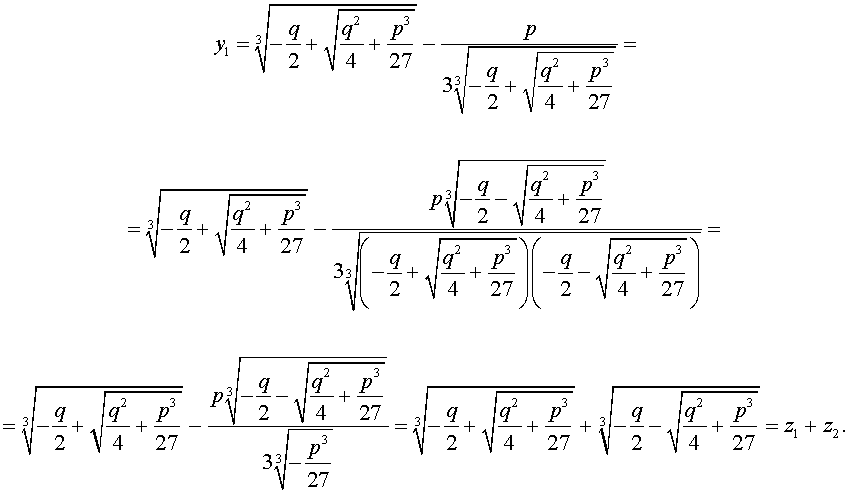
      С другой стороны,

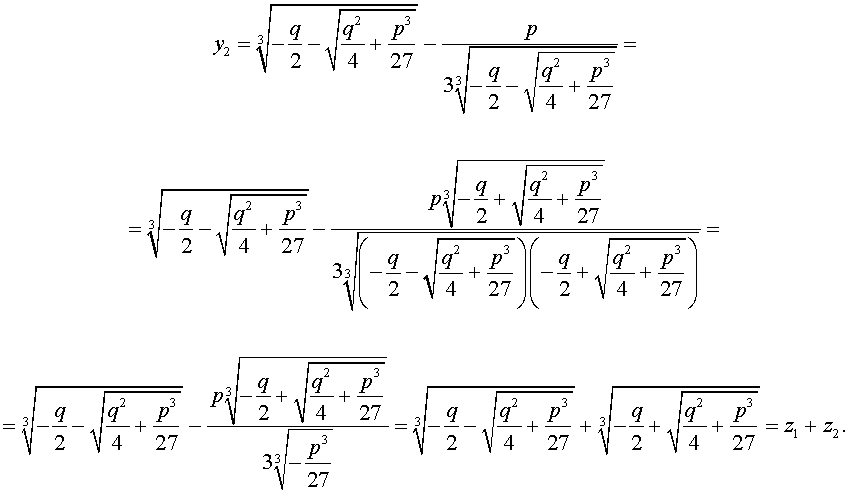
      Таким образом,

и для решения уравнения (5) мы получили формулу

(12)

которая и называется «Формула Кардано».

      Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три  различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).

Пример решения кубического уравнения

      Пример. Решить уравнение

(13)

      Решение. Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену

(14)

      Тогда получим

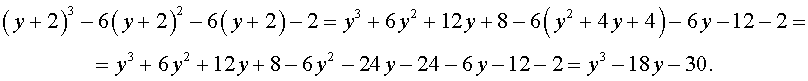
      Следовательно, уравнение (13) принимает вид

		(15)
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену	(16)

      Тогда поскольку

то уравнение (15) примет вид

(17)

      Далее из (17) получаем:

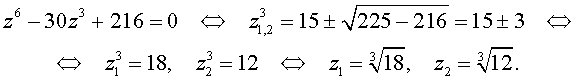
      Отсюда по формуле (16) получаем:

(18)

      Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу

или использовали формулу

      Далее из равенства (18) в соответствии с (14) получаем:

      Таким образом, мы нашли у уравнения  (13) вещественный корень

      Замечание 1. У уравнения (13) других вещественных корней нет.

      Замечание 2.  Поскольку произвольное кубическое уравнение  в комплексной области имеет 3 корня  с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.