
- •Короткі теоретичні відомості.
- •2. Привести постановку задачі відповідно варіанту завдання. 3. Розробити алгоритми і проілюструвати їх структурограмами Насі- Шнейдермана основних
- •Короткі теоретичні відомості.
- •4. Лінійний однозв'язний список.
- •10) З бігу на ковзанах ( чоловіки і жінки на 500 м, 1000 м, 5000 м )
- •Література
Лабораторна робота № 1 Реалізація методів сортування статичних сруктур даних
Мета роботи: 1.Набуття досвіду розробки алгоритмів відтворення сортованих статичних структур даних - масивів. 2.Вдосконалення навичок використання середовища IDE для вводу, тестування і відлагодження програм.
Зміст роботи і звіту. 1.По рекомендованій літературі вивчити і коротко описати основні методи сор- тування масивів - статичних стуктур даних.
2. Привести постановку задачі відповідно варіанту завдання. 3. Розробити алгоритми і проілюструвати їх структурограмами Насі- Шнейдер- мана основних методів сортування запропонованої структури. 4. Реалізувати програмою та привести тексти відтворення цих методів. 5. Розробити тести для перевірки працездатності програми,скласи план і привести в звіті відомості щодо відлагодження програми. 6. Подати результати роботи програми.
Варіанти завдань :
Розробити програму реалізації методів сортування статичних структур даних 1. Вибіром, вставкою , обміном та Шелла сортуваннням.
2. Вибіром, вставкою , обміном та Шейкер-сортуванням. 3, Вибіром, вставкою , обміном та“швидким” сортуванням.
Короткі теоретичні відомості.
Сортуванням
або упорядкуванням списку об’єктів
називається розташування цих об’єктів
за зростанням чи зменшенням згідно
визначенному лінійному відношенню
порядку, такому , як відношення
![]() для чисел. Є два види сортування
: внутрішнеє і зовнішнє. При
внутрішньому впорядкуванні всі
впорядковуючі дані розміщуються в
оперативній пам’яті , де
можна отрима-
ти доступ до даних в
любому порядку ( тобто використовується
модель пам’яті з довільним
доступом ). Зовнішнє впорядкування
використовується тоді, коли об’єм
впорядковуючих даних дуже великий, щоби
всі дані можно було размістити в
оперативну пам’ять. Тут вузьким місцем
є механізм переміщення великіх блоків
даних від устріїв зовнішнего зберігання
даних до опера-
тивної пам’яті і
зворотньо.Далі розглядаються методи
впорядкування в оперативній пам’яті
, тобто внутрішне впорядкування.
для чисел. Є два види сортування
: внутрішнеє і зовнішнє. При
внутрішньому впорядкуванні всі
впорядковуючі дані розміщуються в
оперативній пам’яті , де
можна отрима-
ти доступ до даних в
любому порядку ( тобто використовується
модель пам’яті з довільним
доступом ). Зовнішнє впорядкування
використовується тоді, коли об’єм
впорядковуючих даних дуже великий, щоби
всі дані можно було размістити в
оперативну пам’ять. Тут вузьким місцем
є механізм переміщення великіх блоків
даних від устріїв зовнішнего зберігання
даних до опера-
тивної пам’яті і
зворотньо.Далі розглядаються методи
впорядкування в оперативній пам’яті
, тобто внутрішне впорядкування.
Впорядкування вибіром.
Принцип методу: Знаходиться ( вибирається ) в масиві елемент з мінімальним значенням на інтервалі від 1-го до n-го ( останнього ) елемента і міняється місцями з першим елементом. На другому кроці находиться елемент з мінімальним значенням на інтервалі від 2-го до n-го елемента і міняється місцями з другим елементом. І так далі для всіх елементів до n-1.
Впорядкування за цим методом можна здійсніти, використавши алгоритм, який подається наступною схемою Нассі – Шнейдермана :
-
Для s = 1, n -1


//Пошук мінімального елемента в діапазоні від s –го до n-го min =vect[s] imin = s
Для i = s+1, n
Vect[i]< min так
Min = vect[i] imin = i
Vect[ imin ] = vect[ s ] vect[ s ] = min
Впорядкування вставкою.
Принцип методу : Масив поділяється на дві частини : впорядковану і невпорядковану. Елементі з невпорядкованої частини почергово вибираються і вставляються в впорядковану частину так, щоб не порушити в ній впорядкованість елементів. В початку роботі алгоритму в якості впорядкованої частини масива приймають тільки перший елемент, а в якості невпорядкованої частини – всі залишені елементи. Таким чином, алгоритм буде складатись з n – 1 проходу (n – розмір масива ), кожен з яких буде складатись з чотирьох дій:
Взяття чергового i – го невпорядкованого елемента и збереження його в додатковій змінній;
Пошук позиції j в сортованій частині масиву, в котрій присутність взятого елемента не порушить впорядкованності елементів;
Зсув елемеентів масива від i-1 до j-1 –го вправо, щоб звільнити знайдену позицію вставки;
Вставка взятого елемента в знайдену j -у позицію. Впорядкування за цим методом можна здійсніти, використавши алгоритм, який подається наступною схемою Нассі – Шнейдермана :
-
Для i = 1, n
B = vect [ i ] { взяття несортованого елемента }
{ Цикл пошуку позиції вставки } j =1
Поки B > vect [ j ]
j = j+1
{ Після закінчення циклу індекс j фіксує позицію вставки }
Для k = i – 1, j { цикл зсуву елементів для звільнення позиції вставки }
vect [ k + 1 ] = vect [ k ]
{ Вставка взятого елемента в знайдену позицію} vect [ j ] = B
Впорядкування обміном.
Принцип методу : Зліва направо почергово порівнюються два сусідніх елементи. Якщо їх взаєморозташування не відповідає заданній умові впорядкування, то вони міняються місцями. Далі беруться два наступних елемента і так далі до кінця масиву.
Після одного такого проходу на останній n –ій позиції масива буде стояти максимальний елемент ( “ спливла ” перша “ бульбашка” ). Оскільки максимальній елемент уже стоїть на своїй останній позиції, то другий прохід обмінів виконується до n-1 –го елемента. І так далі. Всього потребується n-1 прохід Впорядкування за цим методом можна здійсніти, використавши алгоритм, який подається наступною схемою Нассі – Шнейдермана :
-
Для k = n, 2

{“ Спливання ” чергового максимального елемента на позицію k }
Для i = 1, k-1
Vect[ i ] > vect{ i+1 ] Так
B = vect[ i ] vect[ i] = vect[ i+1 ] vect[ i+1 ] = B
Впорядкування за методом Шела. Цей метод часто звуть впорядкуванням з спадаючим кроком. На першому кроці впорядковуються елементи n/2 пар ( vect[ i ], vect[ n/2 + i ] ) для 1<= i <= n/2, на другому кроці впорядковуються елементи в n/4 групах із чотирьох елементів ( vect[ i ], vect[ n/4+i ], vect[ n/2+i ], vect[ 3n/4+i ] ) для 1 <=i<= n/4, на третьому кроці впоряд-ковуються елементи в n/8 групах з восьми елементів і так далі.На останньому кроці впорядковуються елементи зразу у всьому масиві. На кожному кроці для впорядкування елементів використовується метод сортування вставками. Впорядкування за цим методом можна здійсніти, використавши алгоритм, який подається наступною схемою Нассі – Шнейдермана :
-
Incr = n div 2
Поки incr > =1
Для i = 1 , n – incr
Vect[ i ] > vect[ i + incr ] так
B= vect[ j ] vect[ j ] = vect[ j+incr ] vectr[ j+incr ] = B
Incr = incr div 2
Шейкер впорядкування.
Недоліком методу простого обміну є те, що елементи з меньшими значеннями швидко займа ють свої позиції ( кожний наступний за один прохід ), а елементи з більшими значеннями пере-міщуються вправо лише на одно місце в кожному проході.Це пов’язано з напрямком прогля-
дання справа наліво. Модернізацією метода простого обміну є сортування зі змінним напрям-
ком проглядань або шейкер – впорядкування, коли використовуються дві анологічні процедури з почерговою зміною напрямків проглядання. В алгоримі відбувається обчислення нових границь проглядань : l =s + 1 і k = s – 1 через фіксацію номера s останнього як лівого, так і правого елементів, які приймають участь в обміні і встановлених на своє місце. Таким чином, як найменші , так і найбільші елементи швидко впорядковуються,займаючи свої кінцеві положення за один відповідний прохід. В залежності від числа N завершення впорядкування відбувається або після проходу справа наліво, або зліва направо по умові зми-кання границь області проглядання l = k.
Впорядкування за цим методом можна здійсніти, використавши алгоритм, який подається наступною схемою Нассі – Шнейдермана :
-
l = 2 k = n s = n
J = k , l
A [ j – 1 ] > A [ j ] так
Swap ( A [ j – 1 ] , A [ j ] ) s = j
l = s + 1
J = l , k
A [ j – 1 ] > A [ j ] так
Swap ( A [ j – 1 ] , A [ j ] )
s = j
k = s - 1
l > k
Швидке впорядкування.
В алгоритмі швидкого впорядкування застосовується метод розбиття з визначенням цент-рального елемента. Розглядається масив з 10 цілих чисел :
А = 800, 150, 300, 600, 550, 650, 400, 350, 450, 700 Масив простягається від індекса low = 0 до індекса high = 9. Його середина припадає на індекс mid = 4. Першим центральнім елементом є A[ mid ] = 550. Таким чином, всі елементи масиву А розбиваються на два підсписка Sl і Sh. Менший з них (Sl ) буде вміщувати елементи менші або рівні центральному. Підсписок Sh.буде вміщувати елементи більші, ніж центральний. Оскільки заздалегідь відомо, що центральний елемент в кінцевому ітогу буде останнім в підсписку Sl, ,тимчасово його пересувають в початок масиву, міняючи місцями з A[ 0 ] ( A[ low ] ). Це дозволяє сканувати підсписок A[ 1 ] – A[ 9 ] за допомогою двох індексів : scanUp і scanDown. Початкове значення scanUp відповідає індексу 1 ( low + 1 ). Ця змінна адресує елементи підсписку Sl. Змінна scanDown адресує елементи підсписку Sh і має початковев значення 9 ( high ). Метою проходу є визначення елементів для кожного підсписку.
550 |
|
150 |
300 |
600 |
800 |
650 |
400 |
350 |
450 |
700 |

scanUp scanDown Оригінальність швидкого впорядкування полягає у взаємодії двох індексів в процесі сканування списку. Індекс scanUp переміщується вверх по списку, а scanDown – вниз.ScanUp просувається вперед і шукається елемент A[ scanUp ] більший , ніж центральний. В цьому місці сканування зупиняється, і йде підготовка до переміщення знайденного елементу в верхній підсписок.Перед тим, як це відбудеться, індекс scanDown пересовується вниз по списку і знаходиться елемент, який є меншим або дорівнює центральному. Таким чином, є два елементи, які знаходяться не в своїх підсписках, і їх треба поміняти місцями. Swap ( A[ scanUP ] , A[ scanDown ] ) ; // поміняти місцями партнерів Цей процес продовжується до тих пір поки scanUp і scanDown не зайдуть один за іншим ( scanUp = 6, scanDown = 5 ). В цей момент scanDown опиняється у підсписку, елементи котрого менші або дорівнюють центральному. Ми попали в точку розбиття двох списків і вказали остаточну позицію для центрального елемента. В цьому прикладі помінялись місцями числа 600 і 450, 800 і 350, 650 і 400.
|
|
150 |
300 |
600 |
800 |
650 |
400 |
350 |
450 |
700 |



scanDown scanUp
Потім відбувається обмін значеннями центрального елементу A[ 0 ] з A[ scanDown ] : Swap ( A[ 0 ], A[ scanDown ] ) В результаті отримався підсписок A[ 0 ] – A[ 4 ] , елементи котрого меньші елементів підсписку A[ 6 ] – A[ 9 ]. Центральний елемент ( 550 ) поділяє два підсписка, кожен з котрих дорівнює приблизно половині початкового списку.
400 |
150 |
300 |
450 |
350 |
550 |
650 |
800 |
600 |
700 |
A

 [
0 ] - A[ 4 ]
A[
6 ] - A[ 9 ]
Для
обробки підсписків використовується
рекурсія. Оба підсписка обробляються
за одним і тиж же алгоритмом.
Підсписок S l
. Підсписок визначається
диапазоном від індекса
low = 0 до high = 4. Його
середина припадає на індекс mid
= 2. Центральним елементом є
A[ mid ] = 300. Поміняти місцями центральний
елемент з A[
low] і присвоїти
початкові значення індексам scanUp
і scanDown:
scanUp = low
+ 1 = 1 scanDown
= high =
4
Сканування вверх припиняється на
індексі 2 ( A
[ 2 ] > центрального елементу ).
Сканування
вниз припиняється на індексі 1 ( A
[ 1 ] < центрального елементу
).
[
0 ] - A[ 4 ]
A[
6 ] - A[ 9 ]
Для
обробки підсписків використовується
рекурсія. Оба підсписка обробляються
за одним і тиж же алгоритмом.
Підсписок S l
. Підсписок визначається
диапазоном від індекса
low = 0 до high = 4. Його
середина припадає на індекс mid
= 2. Центральним елементом є
A[ mid ] = 300. Поміняти місцями центральний
елемент з A[
low] і присвоїти
початкові значення індексам scanUp
і scanDown:
scanUp = low
+ 1 = 1 scanDown
= high =
4
Сканування вверх припиняється на
індексі 2 ( A
[ 2 ] > центрального елементу ).
Сканування
вниз припиняється на індексі 1 ( A
[ 1 ] < центрального елементу
).
Початкове положення Після сканування
300 |
|
150 |
400 |
450 |
350 |
|
300 |
|
150 |
400 |
450 |
350 |
scanUp scanDown scanDown scanUp
Тому що scanDown < scanUp , процес призупиняється. При цьому scanDown є точкою розділення двох ще меньших підсписків : A[ 0 ] і A[ 2 ] – A[ 4 ]. Завершити обробку, помінявши місцями A[ scanDoown ] = 150 і A[ low ] = 300. Положення центрального елементу дає одноелементний і трьохеленментний підсписки. Рекурсивний процес закінчується на пустому або одноелементному підсписку
-
150
300
400
450
350

 A[
0 ] A[ 2 ]
- A[ 4 ]
A[
0 ] A[ 2 ]
- A[ 4 ]
Підсписок Sh.Диапазон підсписку – від індекса low = 6 до high = 9. Його середина припадає на індекс mid = 7. Центральним елементом є A[ mid ] = 800. Подальші дії відбувають анологічно до дій с попереднім підсписком. Рекурсивний алгоритм виконується до утворення пустих або одноелементних підсписків. Впорядкування за цим методом можна здійсніти, використавши алгоритм, який подається наступною схемою Нассі – Шнейдермана :
-
 High
– low < 0
так
н і
High
– low < 0
так
н і
 r
e t u r n
r
e t u r nHigh – low == 1 так
A[ high ] < A[ low ] так
Swap ( S[ low ] , A[ high ] 0 r e t u r n
mid = ( low = high ) / 2
pivot = A[ mid ] / / pivot – робоча змінна
Swap ( A[ mid ], A[ low ] ) scanUp = low + 1 scanDown = high


ScanUp <= scanDown && A[ scanUp ] <= pivot
scanUp + +
Pivot < A[ scanDown ]
scanDown - -
scanUp < scanDown так
Swap ( A[ scanUp ], A[ scanDown ] )
scanUp < scanDown
A[ low ] = A[ scanDown ] A[ scanDown ] = pivot

low < scanDown - 1 так
QuickSort ( A , low, scanDown – 1 )
ScanDown + 1 < high так
QuickSort ( A ,high, scanDown + 1 )
Завдання до захисту лабораторної роботи . Для матриці: 1.Знайти в рядках номер максимального додатнього і добуток від’ємних. 2. Знайти в рядках мінімальний від’ємний та суму додатніх . 3. Знайти в рядках суму від’ємних, розташованих на непарних позиціях, та максимальний за абсолютною величи ною елемент. 4. Знайти в рядках добуток додатніх елементів, які кратні трьом, та номер мінімального від’ємного. 5.Знайти в рядках суму від’ємних та добуток додатніх, які є непарними. 6. Знайти в стовбчиках мінімальний додатній та суму від’ємних. 7. Знайти в стовбчиках добуток від’ємніх елементів, які кратні трьом, та номер мінімального додатнього. 8. Знайти в стовбчиках номер максимального від’ємного і добуток додатніх. 9. Знайти в стовбчиках суму додатніх, розташованих на непарних позиціях, та максимальний за абсолютною величиною елемент. 10. Знайти в стовбчиках суму додатніх та добуток від’ємних, які є непарними.
Лабораторна робота №2 Реалізація напівстатичних структур даних.
Мета роботи: 1. Набуття досвіду розробки алгоритмів відтворення напівстатичних структур даних ( НСД ) : стека, черги та дека. 2. Вдосконалення навичок використання середовища IDE для тестування і відлагодження програми.
Зміст роботи і звіту. 1. Вивчити і коротко описати основні властивості і ознаки НСД .
2. Привести постановку задачі відповідно варіанту завдання. 3. Розробити алгоритми і проілюструвати їх структурограмами Насі- Шнейдермана основних операцій з НСД. 4. Реалізувати алгоритми програмою, остаточний текст якої привести в звіті. 5. Розробити тести для перевірки працездатності програми,скласи план і привести в звіті відомості щодо відлаго дження програми. 6. Подати приклади результів роботи програми.
Завданя : Розробити програму реалізації основних операцій над НСД ( додавання, вилучення ) та над їх інформаційними частинами-рядками ( пошук, вилучення, додавання символів і т.і. ). Варіанти: 1. Стек, черга та дек з обмеженим входом зліва, рядки - вектори з рахівником довжини. 2. Стек, черга та дек з обмеженим входом зправа, рядки - вектори фіксованої довжини. 3. Стек, черга та дек з обмеженим виходом зліва, рядки, - вектори з ознакою кінця-символ %. 4. Стек, черга та дек з обмеженим виходом зправа, рядки - вектори з рахівником довжини. 5. Стек, черга та дек з обмеженим входом зліва, рядки - вектори фіксованої довжини. 6. Стек, черга та дек з обмеженим виходом зправа, рядки - вектори з ознакою кінця-символ %. 7. Стек, черга та дек з обмеженим входом зправа, рядки - вектори з рахівником довжини . 8. Стек, черга та дек , рядки - вектори фіксованої довжини; 9. Стек, черга та дек, рядки - вектори з ознакою кінця – символом %. 10.Стек, черга та дек, рядки - вектори з рахівником довжини.
Короткі теоретичні відомості.
Напівстатичні струтури - це такі,які при опису набувають свого максимального розміру ( N ), а впродовж програми змінюють його при виконанні будь-якої операції. Кількість їх обмежена операціями додавання і вилучення елементів.
Стек – це така напівстатична структура, включення і виключення елементів у який і з якого відбувається тільки з однієї сторони (вершини стека - Тор ). Здійснюється принцип «last-in-first-out” ( останній прийшов-перший вийшов ). Стек дозволяє над собою 2 операції:
1) додавання в стек ( Push ) ;
2) вилучення зі стеку ( Pop ) .
Операції дозволені тільки з одного боку .

 rear N Push
Pop
rear N Push
Pop
п
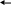
 оточна
довжина m
Top
оточна
довжина m
Top
 m-1
m
m-1
m
 …
…
front 1
Стек використовується для рекурсивних програм. Запам'ятовується стан програми ( значення зміннних, регистрів і т.і. ) перед викликом функции, а по її виконанні повертаються програмі.
У пам'яті стек займає суцільну область. Фізична структура стека доповнюється інформаційним вектором виду:
-
St(код)
Stack(ім'я)
Adr(front)(адреса початку)
Adr(rear)(адреса кінця)
Adr(top)(адреса вершини)
Опис елемента
Елементами стека можуть бути будь-які дані, крім файлового типу.
Опис стека. int StakSize=50;
struct Tstak { Telem Elem[ StakSize}; int top; } Stak;
Додавання
до стеку.
формування
елемента NewElem стеку
так Stak.top==StakSize
ні
Стек
повний Stak.top ++;
Stak.Elem[Stak.top]= NewElem ;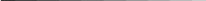



 Вилучення зі
стеку.
Вилучення зі
стеку.
так
Stak.top==-1
ні
Стек
пустий OldElem=
Stak.Elem[Stak.top];
Stak.top -- ;

Черга. Це така структура, додавання елементів у яку дозволяється з одного кінця, а вилучення – з іншого. Принцип “first-in-first-out” ( перший прийшов-перший вийшов ). .

 front
rear
front
rear

 Рор
Push
Рор
Push
Над чергою можна здійснювати ті ж операції, що і над стеком, але з різних сторін ( доступ є тільки до першого й останнього елементів ).
Як фізична структура черга розташовується в пам'яті цільною областю і має визначену максимальну і поточну довжину, що може змінюватися при виконанні програми.
-
Qu
Queue
Adr(imin)(адреса початку)
Adr(front) ( адреса голови )
Adr(rear) ( хвоста )
Adr(imax)(адреса кінця)
Опис елемента
Черга використовується при організації розміщення в пам'яті програм.
Максимальна довжина черги ( N ) повинна бути зазначена на етапі опису.
Черга може бути круговою або кільцевою.
Опис черги. int QueveSize=50;
struct TQueve { Telem Elem[ QueveSize}; int head, tail; } Queve;
Д
формування
елемента NewElem черги
так Queve.tail=QueveSize
ні
Черга повна Queve.tail
++;
Queve.Elem[Queve.tail]= NewElem ;

 одавання
до черги.
Вилучення з
черги.
одавання
до черги.
Вилучення з
черги.
так
Queve.head==-1
ні
Черга порожня
OldElem= Queve.Elem[Queve.head];
Queve. head-- ;
Дек або черга з двома кінцями.
Це така напівстатична структура даних, в якій додавання і вилучення елементів дозволяється з обох боків.
Логічна і фізична структура деку анологічна логічній і фізичній структурі черги. Однак, стосовно до деку доцільно замість "голови" та "хвіст" казати про лівий і правий кінці.Як і для черги , дозволенними операціями над деком є додавання і вилучення елементів, але в ньоому вони дозволяються з обох боків, тобто можна реалізувати додавання і вилучення справа , а також додаваення і вилучення зліва.
Операції над деком:
додавання ліворуч (LPush);
додавання праворуч(RPush);
вилучення ліворуч(LPop);
вилучення праворуч(RPop).



 LPop
RPop
LPop
RPop
Lpush RPush
Як і стек чи черга має максимальну( на етапі опису ) і поточну довжину. Дехто вважає дєк двома чергами, вставленими одна в одну.
Запити до захисту лабораторної роботи.
Визначити поняття напівстатичних структур даних.
Визначення стеку.
Операції , дозволенні над стеком.
Алгоритми операцій над стеком.
Визначення черги.
Операції , дозволенні над чергою.
Алгоритми операцій над чергою.
Визначення деку.
Операції , дозволенні над деком.
Алгоритми операцій над деком.
Лабораторна робота № 3 Програмування динамічних сруктур даних Мета роботи: 1. Набуття досвіду розробки алгоритмів відтворення динамічних структур даних: стеків, черг та списків. 2. Вдосконалення навичок використання середовища IDE для вводу, тестування і відлагодження .
Зміст роботи і звіту. 1. По рекомендованій літературі вивчити і коротко описати основні властивості і ознаки
динамічних стуктур даних.




 550
550