
Принцип даламбера
Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид:
 ,
,
 -
равнодействующая активных сил,
-
равнодействующая активных сил,
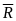 - равнодействующая сил реакции связей.
- равнодействующая сил реакции связей.
Силой
инерции материальной точки
называют произведение массы точки на
вектор ускорения, взятое с обратным
знаком, т.е.
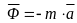 .
.
Если
использовать понятие силы инерции, то
основной закон динамики принимает
вид: 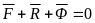
Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил.
Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.
Общее уравнение динамики
Общее
уравнение динамики ![]() –
при движении системы с идеальными
связями в каждый данный момент времен
сумма элементарных работ всех приложенных
активных сил и всех сил инерции на любом
возможном перемещении системы будет
равна нулю. Уравнение использует принцип
возможных перемещений и принцип Даламбера
и позволяет составить дифференциальные
уравнения движения любой механической
системы. Дает общий метод решения задач
динамики.
–
при движении системы с идеальными
связями в каждый данный момент времен
сумма элементарных работ всех приложенных
активных сил и всех сил инерции на любом
возможном перемещении системы будет
равна нулю. Уравнение использует принцип
возможных перемещений и принцип Даламбера
и позволяет составить дифференциальные
уравнения движения любой механической
системы. Дает общий метод решения задач
динамики.
Обобщенные силы
оБОБЩЕННЫЕ СИЛЫ - величины Qi, произведения к-рых на элементарные приращения обобщённых координат qi системы дают выражение элементарной работы действующих на систему сил. Т. о., выражение элементарной работы сил, действующих на систему с sстепенями свободы, через О. с. имеет вид
![]()
Обобщенные координаты
независимые между собой параметры qi (r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механич. системы и которые однозначно определяют положение системы. Закон движения системы в О. к. даётся s уравнениями вида qi = qi (t), где t— время. О. к. пользуются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение.
Лагранж 2 рода
Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения механической системы, составленные в обобщённых координатах:
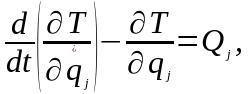
где
j
– количество уравнений (j
= 1, 2, …, n),
n
– число степеней свободы механической
системы, T
– кинетическая энергия системы, qj
– обобщённая координата,
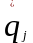 – обобщённая скорость, Qj
– обобщённая сила. Если qj
= x
(м), то
– обобщённая скорость, Qj
– обобщённая сила. Если qj
= x
(м), то
 (м/с);
если qj
= φ
(рад), то
(м/с);
если qj
= φ
(рад), то
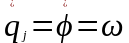 (рад/с).
(рад/с).
