Розрахунок таврових з'єднань.

У таврових з'єднаннях із попередньою підготовкою кромок напруження в швах визначають так, як і для су­цільних деталей, але порівнюють ці напруже–ння із допустимими напру­женнями для зварних швів.

Для таврових з'єднань, здійснених кутовими зварними швами без підго­товки кромок, розрахунок на міцність виконують за напруженням зрізу в зварних швах. Згідно зі схемою навантаження таврового з'єднання (рис. 15.10) максимальне напруження зрізу має місце в точках верхніх кін­ців швів.

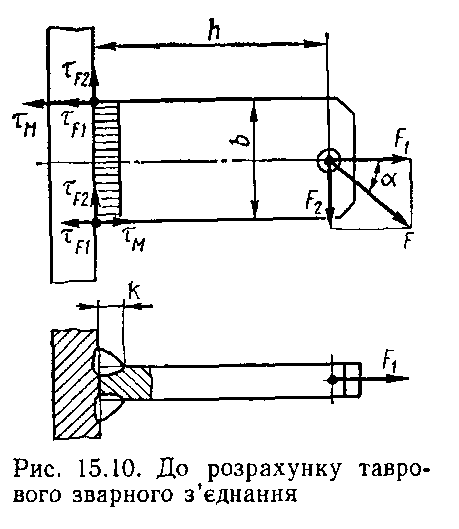
Це напруження дорівнює сумі напружень від дії двох складових сили F на двох взаємно перпендикулярних напрямах

F₁ = F cosα, F₂ = F sinα та моменту Μ = F₂h.

Для двох швів таврового з'єднання

τ_F1 = F₁/(2∙0,7kb); τ_F2 = F₂/(2∙0,7kb); τ_Μ = M/(2W₀) = 3M/(0,7kb²).

У виразі для τ_Μ величина W₀ = 0,7kЬ²/6 – осьовий момент опору перерізу одного шва в площині його руйнування.

Відповідно умову міцності такого таврового з'єднання записують у вигляді

τ_mах = √( τ_F1 + τ_Μ)² + τ²_F2 ≤ [τ]'. (6)

Для частинного випадку навантаження, наприклад при α = 0, ді­стають

F_l = F; F₂ = 0; Μ = 0 і τ = τ_F = F/(2 · 0,7kb) ≤ [τ]'.

Сили, які діють в зачепленні косозубих циліндричних передач

Номінальні сили у зачепленні циліндричних коліс. У навантаженій зубчастій передачі сила взаємодії зубців розподілена вздовж їхнього контакту. Цю розподілену силу замінимо зосередженою силою, при­кладеною до зубця у середньому нормальному його перерізі. Силами тертя, що виникають у результаті ковзання профілів зубців, можна знехтувати, оскільки коефіцієнт тертя в зоні контакту малий, і тому таке припущення не впливає практично на кінцевий результат.

На рис. 23.6, а показане косозубе зубчасте колесо, яке наванта­жене обертовим моментом Т₁. Зубці цього колеса взаємодіють із зуб­цями спареного зубчастого колеса. Схема взаємодії зубців показана у їх середньому нормальному перерізі А–А.

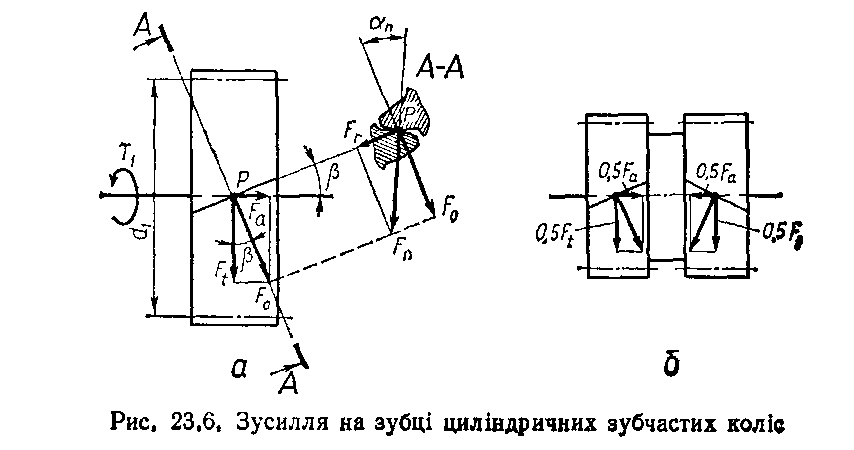
Сила F_n направлена вздовж нормалі до профілів зубців у точці їх контакту, тобто вздовж лінії зачеплення, яка утворює кут зачеп­лення α_n із перпендикуляром до лінії центрів коліс. Силу F_n замі­нимо двома її взаємно перпендикулярними складовими F_r і F₀, які перенесемо на схему колеса. Тут сила F_r проекціюється у точку Р, а сила F₀ направлена перпендикулярно до лінії зубця. Тепер силу F₀ також замінимо двома її взаємно перпендикулярними складовими F_t і F_a.

Отже, замість однієї нормальної сили F_n на зубець маємо три вза­ємно перпендикулярні її складові F_t, F_a і F_r, Таке зображення сил, що діють на зубці у зачепленні, зручне для розрахунків зубчастої передачі, її валів та їхніх опор.

Сила F_t , яку будемо називати коловою силою, лежить у площині дії обертового моменту Т₁ і направлена по дотичній до ділильного кола зубчастого колеса. Тому

F_t = 2Т₁/d₁. (23.15)

Складова F_a, яка перпендикулярна до площини колеса і пара­лельна осі його вала, називається осьовою силою. Вона може бути ви­ражена через F_t та кут нахилу зубцівβ F_a = F_t · tgβ. (23.16)

Сила F_r діє у площині колеса і направлена вздовж його радіуса, тому її називають радіальною силою. Для визначення F_r попередньо знайдемо F₀ = F_t /cos β, а тоді (див. переріз А–А на рис. 23.6, а) запишемо

F_r = F₀· tg α_n = F_t · tg β_n /cosβ. (23.17)

Нормальна сила F_n до профілів зубців дорівнює геометричній сумі сил F_t, F_a і F_r.

Модуль цієї сили можна визначити за формулою

F_n = F₀/cos α_n = F_t / (cosα_n· cos β), або F_n = 2T₁/(d₁ cosα_n · cos β). (23.18)

У разі зачеплення прямозубих коліс (β = 0) колова сила також визначається за формулою F_t = 2Т₁/d₁, осьова сила F_а = 0, а радіальна сила може бути знайдена за формулою F_r = F_t· tgα. (23.19)

Наявність осьової сили F_a у зачепленні косозубих коліс, що до­датково навантажує вали та їхні опори, обмежує використання косо­зубих коліс із великим кутом нахилу лінії зубців β (F_а зростає із збільшенням β). Цього недоліку позбавлені шевронні зубчасті пере­дачі, де осьові сили у зачепленні взаємно зрівноважуються (рис. 23.6, б), бо лівий та правий півшеврони мають протилежний на­хил зубців. Цим пояснюється можливість збільшення кутів нахилу зубців у шевронних колесах у порівнянні з косозубими. Колова та радіальна сили у зачепленні шевронних зубчастих коліс визнача­ються відповідно за формулами F_t = 2Т₁/d₁ і F_r = F₀ · tg α_n = = F_t · tg β_n /cosβ.