4.2. Застосовність до грунту рішень теорії пружності

При визначенні напружень у масиві грунту використовуються закони механіки для

пружного суцільного тіла. Наскільки грунти задовольняють даним вимогам?

Доказ застосовності теорії пружності до грунтів (постулати теорії

пружності).

2. Теорія пружності розглядає тіла пружні.

У грунтах спостерігаються великі залишкові деформації Sост. Але для будівельників су-

щественно одноразове завантажені підстави, тобто тут умова пружності застосовно

(а в загальному випадку немає). Цій умові задовольняють задачі визначення напруг і

деформацій в основі зводяться споруд. Підстави відчувають переваги-

але одноразове завантажені під час зведення споруди (як правило, без розвантаження).

Крім того, при дії вертикальних сил, спрямованих вниз, в них виникають переваг

щественно деформації стиснення. Тому рішення теорії пружності можуть бути вико-

ни для розгляду зазначених завдань.

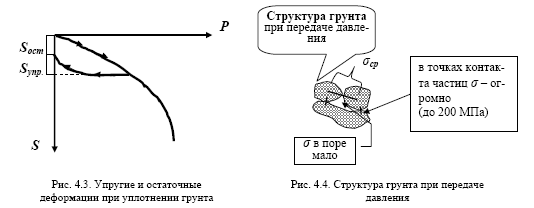
3. Теорія пружності розглядає тіла суцільні.

Внаслідок зернистості грунту встановити справжнє напруга, що у ка-

кой-якій точці його масиву, з використанням теорії пружності неможливо. Доводиться

обмежуватися визначенням середньої інтенсивності напруги σср в необхідній точці ос-

вання, приймаючи умовно, що грунт є суцільним тілом. У точках контактів частинок

напруги будуть у багато разів більше середніх значень. У цьому випадку можна говорити про «суцільно-

ності »грунтів.

4. Теорія пружності розглядає тіла ізотропні.

Іноді грунти володіють анізотропією, зумовлену як характером їх утворення,

так і попереднім напруженим станом. Проте при вирішенні інженерних

завдань з деяким наближенням зазвичай приймають, що грунти ізотропні. Це в багатьох

випадках близько до дійсності (для пісків, неслоістимі глин і суглинків та т. п.). При

необхідності можна врахувати анизотропность грунтів, але це призводить до ускладнення рас-

Четово.

(Будемо вважати, з відомими допущеннями, що грунт - ізотропне тіло).

Таким чином, при визначенні напружень в масиві приймають, що грунт-

ється суцільним лінійно-деформується тілом, що зазнають одноразове завантажений-

ня. При цих умовах для визначення осереднених напружень в точці масиву грунту

використовують рішення теорії пружності.

4.3. Напруження, що виникають від дії зовнішніх навантажень. Дія

зосереджених сил, розподіленого навантаження. Дія рівномірно

розподіленого тиску, метод кутових точок

Проблеми розподілу напружень в грунтовому масиві розглядаються у фазі його

ущільнення. Фаза ущільнення є стадією його напружено-деформованого стану

ня, що представляє найбільший інтерес для практики, тому що при реальному проектування

нии напруги в грунтовому масиві обмежуються величиною, незначно пере-

шує початкове критичне тиск. Найважливішим наслідком принципу лінійної де-

формируемости, застосовність якого знаходиться в діапазоні напруг, відповідних

щих фазі ущільнення, є правомірність використання для аналізу напружено-

деформованого стану грунтового масиву апарату теорії пружності. При цьому в

зазначеному аналізі модуль пружності повинен бути замінений на модуль деформації, ком-

комплексно враховує розвиток як пружних, так і пластичних деформацій грунту. В об-

щем випадку завдання про розподіл напружень в грунтовому масиві при заданих крайових

умовах може бути зведена до вирішення диференціальних рівнянь рівноваги, до-

наних рівняннями спільності деформацій та фізичними рівняннями у формі закону

Гука. Такі завдання, як правило, вирішуються чисельними методами, оскільки отримання для

них замкнутих аналітичних рішень є досить проблематичним (подинтегральних

функції не є, як правило, повними диференціалами). З цієї причини представ-

ляють особливий практичний інтерес аналітичні рішення, отримані з використанням

тільки рівнянь рівноваги на підставі спрощують гіпотез. До таких рішень відно-

сится широко відома в механіці грунтів завдання Буссінеска про розподіл напруг

в пружному півпросторі від дії вертикальної зосередженої сили на граничній

площині. Представляють практичний інтерес не стільки вирішення зазначеної задачі,

скільки її застосування. Використовуючи принцип суперпозицій, вирішені завдання про розподіл

напружень в грунтовому масиві при довільній навантаженні на граничній площині напів-

простору, засновані на інтегруванні рішення Буссінеска.

Визначення напружень Z σ в масиві грунту при дії одиничної верти-

кальной сили N, прикладеної до кордону грунтової основи.

Рішення завдання Буссінеска. Засноване на наступних гіпотезах (згодом під-

дження точними рішеннями):

а) нормальні напруження на площадках, дотичних до сферичної поверхні з

центром в точці прикладання сили, є головними напруженнями. З цієї причини ка-

сательние напруги на зазначених майданчиках відсутні;

б) нормальні напруження, що лежать у вертикальній площині, на майданчиках, нор-

мальних до сферичної поверхні з центром в точці прикладання сили, рівні нулю;

в) нормальні напруження на площадках, дотичних до сферичної поверхні з

центром в точці прикладання сили, прямо пропорційні косинусу кута видимості і про-

ратно пропорційні квадрату радіуса сфери. Під кутом видимості розуміється кут

між радіусом сфери, проведеним у центр майданчика, і центральної вертикальної

віссю сфери.

Постульованих гіпотези дозволяють отримати замкнуті аналітичні рішення про

розподілі напружень в півпросторі від дії вертикальної сили на його гра-

ниці, засновані виключно на рівняннях рівноваги. Рішення завдання пояснюється

графічними побудовами на рис. 4.5, на якому представлені вертикальний розріз по-

лупространства і його перетину горизонтальними площинами.

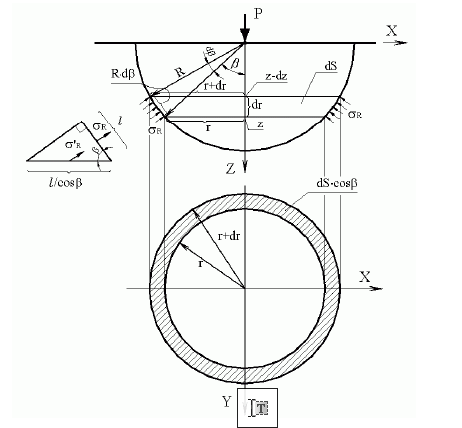
Початок прямокутної декартової системи координат розмістимо в точці прикладання

вертикальної сили Р на кордоні півпростору. Вісь z спрямуємо по вертикалі вниз, вісь

x - по горизонталі вправо, а вісь y - перпендикулярно площині креслення. Щодо на-

чала осей координат побудована полусфера радіусом R, перетин якої з вертикальною

площиною, що проходить через центральну вісь, утворює півколо такого ж радіу-

са. У перетині півсфери горизонтальною площиною на глибині z утворюється коло

радіусом r. Кут видимості радіуса r на вертикальному розрізі позначимо β.

У перетині півсфери горизонтальною площиною на глибині z - dz утворюється коло

радіусом r + dr з кутом видимості на вертикальному розрізі β + dβ. Розглянемо рівновагу

сферичного кільця, виділеного з півсфери двома горизонтальними площинами на

глибині z і z - dz. З урахуванням того, що довжина твірної сферичного кільця дорівнює R · dβ,

площа його поверхні визначиться формулою: S = 2 ⋅ π ⋅ r ⋅ R ⋅ dβ. На поверхні сферіче-

ського кільця діють нормальні напруження σR, а дотичні напруги, у відповідних

вии з гіпотезою а), відсутні. Знайдемо напруги σR з умови рівноваги проекцій

всіх сил, що діють по поверхні півсфери радіусом R, на вертикальну вісь z.

Відповідно до гіпотези в), σR = A cosβ/R2. Крім цього, r = R ⋅ sinβ. Підставляючи в

рівняння (3.1) вирази для σR і r і виконуючи перетворення, отримаємо:

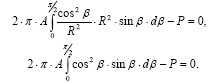
Виконуємо заміну змінних в рівнянні (4.2): u = cosβ, du = - sinβ ⋅ dβ. продовжуючи

перетворення, отримаємо вираз для невизначеного коефіцієнта А:

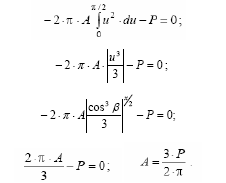
Висловимо cosβ через ординату z: cosβ = z / R. З урахуванням цього, формула для визначення

напруги σR буде мати вигляд

Практичний інтерес представляють напруги на горизонтальній площадці, наклейте-

ненной до майданчика, на якій діють напруги σR, під кутом β. Відповідно до ги-

потезой б) головний вектор напруг на горизонтальній площадці σ'R збігається за на-

правлінню з вектором напруги σR, а його модуль дорівнює σ'R = σR ⋅ cosβ. проекції головного

вектора напружень σ'R на координатні осі є компонентами тензора напруг

на горизонтальній площадці. Оскільки головний вектор напруг σ'R збігається за на-

правлінню з радіусом вектором R, напрямні косинуси вектора напружень визначаються-

ються формулами:

З урахуванням отриманих вище залежностей, компоненти тензора напружень на

горизонтальній площадці будуть визначатися формулами

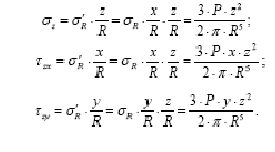
Формулу для σz зазвичай табуліруйте. Для цього виконують такі перетворення:

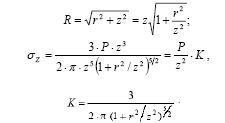
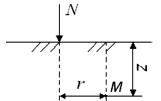Надалі для практичних розрахунків розрахунок-

ву схему завдання призводять до простішого виду (рис.

4.6). Вертикальні напруги в розрахунковій точці М оп-

ределяют за формулою

Коефіцієнт К, що залежить від безрозмірного па- раметра r / z, наводиться в довідкових даних. Z - глибина точки; r - відстань від точки до лінії дії сили; М - розглянута точка; N - зосереджена вертикальна сила.

Визначення напружень в масиві грунту від дії кількох вертикаль-

них зосереджених сил, прикладених до кордону грунтової основи (принцип

Сен-Венана - принцип незалежності дії сил).

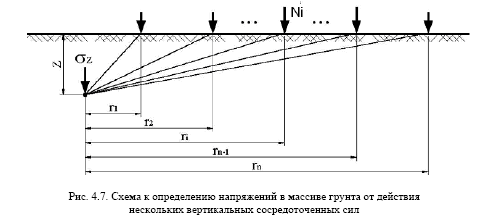
Якщо до поверхні ізотропного лінійно-деформівного півпростору прог-

жено декілька сил (N1, N2, ..., Nn), то при прямій пропорційності між напруги-

ми і деформаціями можна використовувати принцип суперпозиції і знайти значення σz в лю-

бій точці М простим підсумовуванням:

Коефіцієнт К, що залежить від безрозмірного параметра r / z, визначається так само як і

в попередньому випадку.

Визначення напружень σz в масиві грунту при дії будь розподілений-

ної навантаження, прикладеної до кордону грунтової основи (метод елементарного сум-

мування).

Нехай до поверхні ізотропного лінійно-деформівного півпростору в пре-

справах площі завантаження докладено розподілене тиск. завантажену площа

можна розбити на невеликі прямокутники та більш складні фігури по її контуру.

З деяким наближенням тиск, розподілене в межах i-гo прямокутника,

можна замінити рівнодіючої Ni, прикладеної в центрі ваги цього тиску. вер-

тікальное стискальне напруження від дії сили Ni складе:

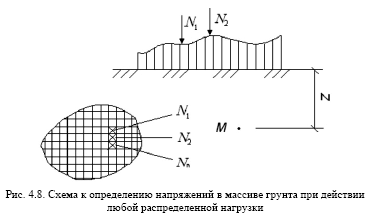
Визначивши величину σzi від навантаження кожної з невеликих фігур, на які розбита

площа завантаження, і провівши підсумовування цих напруг, визначимо напругу

σzi від дії розподіленого навантаження (аналогічно формулі 4.9):

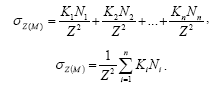
Цей метод також іноді називають методом елементарних квадратів.

Коефіцієнт К, що залежить від безрозмірного параметра r / z, визначається так само як і

в попередніх випадках.

Точність розрахунку збільшується зі зменшенням розмірів окремих елементів, одна-

до при великому числі елементів значно збільшується трудомісткість завдання.

Визначення напружень σz при дії місцевого рівномірно розподіленого

тиску (метод кутових точок).

Якщо закон розподілу тиску по поверхні ізотропного лінійно-

деформованого півпростору відомий, то елементарне підсумовування можна замінити

нитка інтеграцією. - При розгортанні цього інтеграла виходить дуже громіздка

формула, тому при рівномірно розподіленому тиску після інтегрування по пря-

моугольной площі завантаження значення для точок, розташованих під центром прямо-

вугільної площі завантаження (рис. 4.9, а), отримаємо:

Де - Приймається за таблицею 4.2; Р - рівномірно розподілене тиску.

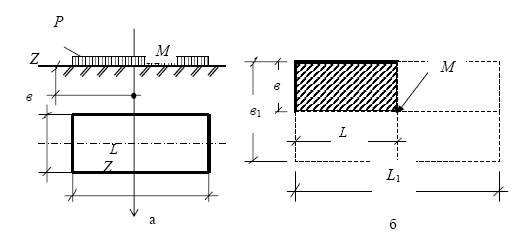Рис. 4.9. Розрахункові схеми до визначення напружень Z σ при дії місцевого рівномірно розподіленого тиску: а - для точок, розташованих підцентром прямокутної площі завантаження; б - під кутовими точками прямокутної площізавантаження

При знаходженні Z σ під кутовими точками прямокутної площі завантаження (на-

приклад, під точкою М) (рис. 4.9, б), значення також мож-

але приймати за таблицею 4.2.

Напруга під кутовими точками визначають за формулою

Для визначення вертикального напруги Z σ в будь-якій точці півпростору мож-

але скористатися виразом Z σ = 0,25 ⋅ α 'Р. Дійсно, якщо проекція розглядає-

ваемой точки М 'на горизонтальну поверхню півпростору (точка М) розташовується

в межах площі завантаження (рис. 4.10, а), то цю площу можна розбити на чотири пря-

моугольніка (I - Meaf, II - Mfbg, III - Mgch, IV - Mhde) так, щоб точка М була кутовий

точкою кожного з них.

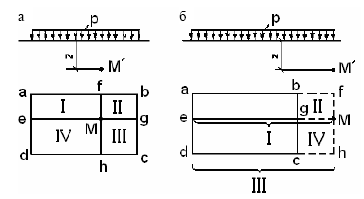
Рис. 4.10. Розрахункові схеми до визначення напружень Z σ при дії місцевого рівномірно рас-

пределеніе тиску: а - для точок, розташованих усередині прямокутної площі завантаження;

б - під точками, розташованими поза прямокутної площі завантаження

Таблиця 4.2

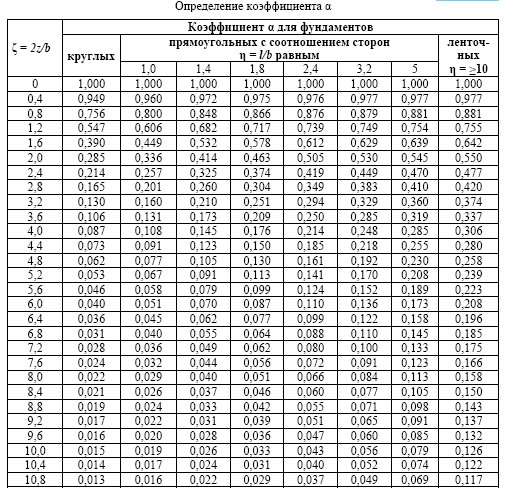
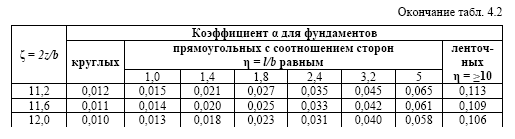
Тоді напруга Z σ знайдемо підсумовуванням напруг під кутовими точками че-

тирех площ завантаження:

де

α1, α2, α3, α4 - коефіцієнти, що приймаються за таблицею в залежності від ставлення

сторін площ завантаження I, II, III, IV і відносини Z (глибини розташування точки М ') до

ширині кожної з цих площ.

Коли проекція точки М 'на горизонтальну поверхню півпростору (точка М)

розташовується поза межами площі завантаження (рис. 4.6, б), точку М аналогічно можна

представити як кутову точку фіктивних площ завантаження I, II, III, IV. При цьому в

межах площ II і IV фіктивна навантаження прикладається в зворотному напрямку.

Напруга визначається за вираженім

Узагальнюючи формули, можна дати таке визначення методу кутових точок: на-

напруга в довільній точці від навантаження, розподіленої по прямокутній пло-

щади, так само алгебраїчній сумі напруг в кутових точках прямокутників,

для яких розглянута точка є кутовий, при цьому алгебраїчна сума

площ цих прямокутників з урахуванням знаків у формулі підсумовування напруги-

ний повинна збігатися з фактичною площею навантаження.

Так, користуючись методом кутових точок, можна знайти напруга σ

z в будь-якій точці по-

лупространства, до поверхні якого прикладена рівномірно розподілене навантаження в

межах прямокутної площі.