Введение
Для количественного определения кислородного потенциала газовой фазы необходимо знать равновесный состав образовавшейся атмосферы и парциальные давления ее составляющих, а также способность к окислению или восстановлению материала, подвергаемого воздействию данной газовой фазы. Следовательно, окислительно-восстановительные свойства равновесной газовой фазы являются относительными и зависят также от термодинамических характеристик обрабатываемого ею материала.
В атмосферах, образующихся в металлургических агрегатах и системах, обычно присутствуют одновременно несколько газообразных веществ, способных реагировать с кислородом, и образуется несколько продуктов. Таким образом, возникают сложные газовые атмосферы . Их термодинамический анализ основывается на известном положении, утверждающем, что сложное равновесие достигается лишь при одновременном достижении всех возможных в системе частных равновесий.
Подачу газообразного кислорода к металлу струями дутья осуществляют практически во всех современных процессах окислительного рафинирования металлов. Окислительное рафинирование широко используют при получении сплавов железа (сталей), а также при удалении примесей из меди, свинца, никеля, олова и ряда других металлов.
1. Кислородный потенциал равновесной газовой фазы.
Количественной
характеристикой окислительно-восстановительных
свойств равновесной газовой фазы
является ее кислородный потенциал
,
который представляет собой величину
химического потенциала молекулярного
кислорода
,
отсчитываемого от стандартного состояния
,
где парциальное давление кислорода
равно 1.
(1.1)
Величина химического
потенциала
данной газовой атмосферы равна частной
производной от изменения энергии Гиббса
по числу молей кислорода при сохранении
постоянными температуры, давления и
числа молей остальных составляющих
газовой фазы j:
(1.2)
Величина
зависит от температуры, а также от
состава газовой атмосферы, выражаемого
отношением равновесных парциальных
давлений реагентов, влияющих на
.
Так, для реакции
уравнение кислородного потенциала в
зависимости от температуры и отношения
парциальных давлений
получается следующим образом:
;
;
;
;
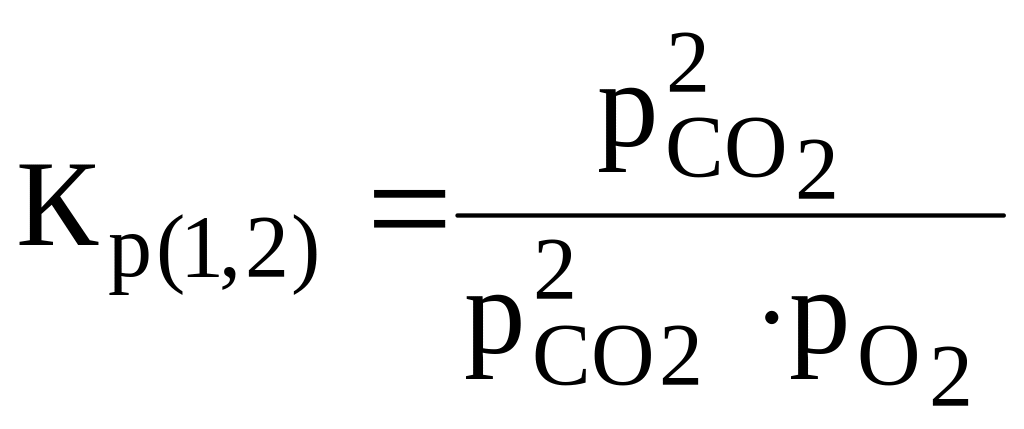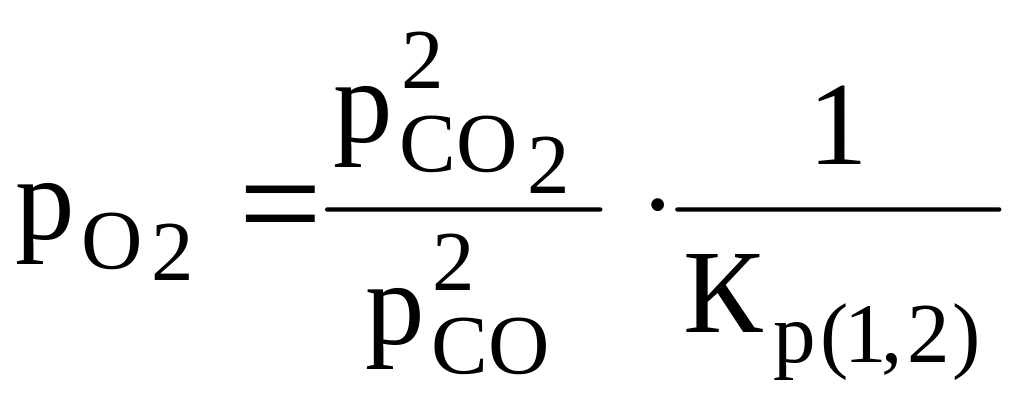(1.3)
При постоянном
заданном отношении
величина кислородного потенциала
газовой фазы линейно зависит от
температуры. В числовом выражении,
удобном для графического представления
параметров
,
а также
,
уравнение
легко получить, введя в уравнение (1.3)
температурную функцию
,
а также значения газовой постоянной
и модуля перехода от натуральных
логарифмов к десятичным 2,303. Тогда
величина параметров может отличаться
на целое число порядков.
Расчетное уравнение имеет вид:
Дж (1.4)
Для определения
при заданной температуре и заданном
можно использовать график рис.1 . Он
соответствует уравнению (1.4) с параметрами
и
.
При (
)>
с повышением температуры
возрастает, а при (
)<
убывает. При (
)=1
равен стандартному изменению энергии
Гиббса реакции
.
Как уравнение (4)
так и график рис.1 могут быть применены
для определения
,
если известны конечные (равновесные)
отношения
и
или
.
При задании лишь исходных (неравновесных)
их величин необходимо провести расчет
равновесных значений, используя анализ,
приведенный выше. Неравномерность
газовой фазы может быть установлена
при заданных Т,
,
и из Т,
.
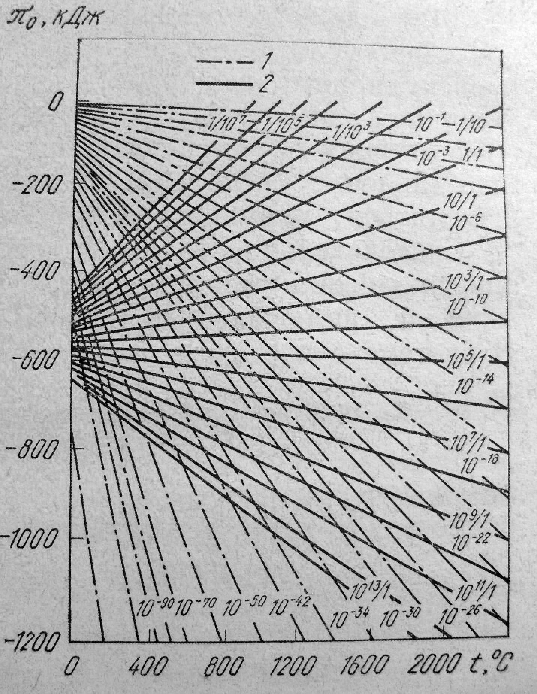
Рис.1. Зависимость
кислородного потенциала газовой фазы
от температуры для различных значений
(1)
и
(2)