
V1: Эконометрика
V2: Метод наименьших квадратов
V3: Предпосылки МНК, методы их проверки
(Задание с выбором одного правильного ответа из предложенных)
I: {1}, K=A;
S: Для линейной
регрессионной модели
![]() гетероскедастичностью называют свойство
дисперсии случайного отклонения при
переходе от наблюдения к наблюдению
проявлять ...
гетероскедастичностью называют свойство
дисперсии случайного отклонения при
переходе от наблюдения к наблюдению
проявлять ...
-: постоянство ;
-: стремление к нулю ;
-: изменчивость ;
-: стремление к единице.
I: {2}, K=B;
S: Регрессионные остатки и объясняющая переменная в линейной регрессионной модели независимы друг от друга ...
-: условием линеаризации;
-: нарушением предпосылок метода наименьших квадратов;
-: признаком гетероскедастичности остатков;
-: одной из предпосылок метода наименьших квадратов.
I: {3}, K=A;
S: Гетероскедастичность будет играть существенную роль в построении эконометрической модели в случае, когда значения результирующей переменной ...
-: слабо варьируются;
-: независимы от объясняющих переменных;
-: сильно варьируются;
-: постоянны.
I: {4}, K=A;
S: При наличии автокорреляции остатков, вызванной неучтенным в модели фактором, следует определить фактор, являющийся причиной этого и ...
-: исключить его из уравнения регрессии;
-: прибавить к результативной переменной;
-: приравнять к нулю;
-: включить его в уравнение регрессии.
I: {5}, K=A;
S:
По графику зависимости остатков e
от теоретических значений зависимой
переменной y'
можно судить, что причиной автокорреляции
остатков является…

-: наличие ошибок измерений переменных;
-: неправильная спецификация модели;
-: мультиколлинеарность данных;
-: случайный характер остатков.
V3: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
(Задание с выбором нескольких правильных ответов из предложенных)
I: {1}, K=A;
S: Несмещенность оценки характеризуется …
-: равенством нулю математического ожидания остатков ;
-: отсутствием накопления остатков при большом числе выборочных оцениваний;
-: зависимостью от объема выборки значения математического ожидания остатков;
-: максимальной дисперсией остатков.
I: {2}, K=B;
S: Если оценка параметра эффективна, то это означает …
-: возможность перехода от точечного оценивания к интервальному;
-: наименьшую дисперсию остатков;
-: уменьшение точности с увеличением объема выборки;
-: невозможность перехода от точечного оценивания к интервальному.
I: {3}, K=A;
S: Практическая значимость свойств несмещенности, эффективности и состоятельности оценок параметров, полученных при помощи метода наименьших квадратов выражается в …
-: возможности перехода от точечного оценивания к интервальному ;
-: уменьшение точности с увеличением объема выборки;
-: отсутствии накопления остатков при большом числе выборочных оцениваний;
-: накоплении значений остатков при большом числе выборочных оцениваний.
I: {4}, K=A;
S: Если оценки параметров уравнения регрессии, полученных при помощи метода наименьших квадратов обладают свойствами несмещенности, эффективности и состоятельности, то …
-: возможен переход от точечного оценивания к интервальному;
-: математическое ожидание остатков равно нулю и они характеризуются минимальной дисперсией;
-: наблюдается уменьшение точности оценивания параметров с увеличением объема выборки;
-: происходит накапливание значений остатков при большом числе выборочных оцениваний.
I: {5}, K=A;
S: Нарушение предпосылок метода наименьших квадратов ведет к нарушению свойств __________ оценок параметров уравнения регрессии.
-: эффективности;
-: несмещенности;
-: несостоятельности;
-: оперативности.
V2: Метод наименьших квадратов
V3: Обобщенный метод наименьших квадратов (ОМНК)
(Задание с выбором двух правильных ответов из предложенных)
I: {1}, K=A;
S: Укажите назначение применения статистики Дарбина-Уотсона:
-: проверяет гипотезу о наличии автокорреляции только первого порядка;
-: используется только для линейных моделей;
-: не применим для проверки автокорреляции в остатках;
-: не применим к моделям с лаговыми переменными.
I: {2}, K=B;
S: Для проверки наличия гетероскедастичности остатков служат:
-: статистика Дарбина-Уотсона;
-: графический метод;
-: тест Голдфелда-Квандта;
-: метод скользящей средней.
I: {3}, K=A;
S: К методам устранения автокорреляции остатков не относятся:
-: метод Кохрана-Оркатта;
-: традиционный метод наименьших квадратов;
-: метод Голдфелда-Квандта;
-: обобщенный метод наименьших квадратов.
I: {4}, K=A;
S: Обобщенный метод наименьших квадратов может применяться в случае нарушения предпосылки МНК о _______ остатков.
-: гомоскедастичности;
- : максимизации суммы квадратов;
-: существовании автокорреляции;
-: отсутствии автокорреляции.
I: {5}, K=A;
S: Обобщенный метод наименьших квадратов может использоваться для корректировки _______ остатков.
-: автокорреляции ;
-: доверительного интервала;
-: стандартной ошибки;
-: гетероскедастичности.
V3:Оценка тесноты связи
(Задание с выбором двух правильных ответов из предложенных)
I: {1}, K=A;
S: Коэффициент парной корреляции можно рассчитывать для оценки тесноты связи между …
-: зависимым и независимым параметрами;
-: двумя независимыми параметрами;
-: зависимой и независимой переменными;
-: двумя независимыми переменными.
I: {2}, K=B;
S: Значение
коэффициента детерминации, рассчитанное
для линейного уравнения парной регрессии
составило
![]() .
Следовательно, значение линейного
коэффициента парной корреляции
.
Следовательно, значение линейного
коэффициента парной корреляции
![]() может быть равно …
может быть равно …
-: - 0,9; если b < 0;
-: –0,09; если b < 0;
-: 0,09; если b > 0;
-: 0,9; если b > 0.
I: {3}, K=A;
S: Значение линейного коэффициента корреляции не может характеризовать тесноту связи для уравнения …
-:
![]() ;
;
-:
![]() ;
;
-: ;
-: .
I: {4}, K=A;
S: В качестве показателя тесноты связи для уравнения регрессии может использоваться …
-: F- критерий Фишера;
-: коэффициент парной корреляции;
-: коэффициент множественной корреляции;
-: t-критерий Стьюдента.
I: {5}, K=A;
S: Для зависимости спроса на некоторый товар от цены за единицу товара и дохода потребителя получено уравнение регрессии вида . Парными коэффициентами корреляции могут быть
-:
![]() ;
;
-:
![]() ;
;
-:
![]() ;
;
-:
![]() .
.
V3: Оценка качества подбора уравнения
(Задание с выбором одного правильного ответа из предложенных)
I: {1}, K=A;
S: Значение коэффициента детерминации составило 0,81, следовательно уравнением регрессии объяснено _____ дисперсии зависимой переменной.
-: 81 %;
-: 0,81 %;
-: 19 %;
-: 0,19 % .
I: {2}, K=B;
S: Отношение дисперсии результирующего признака, объясненной уравнением регрессии, к его общей дисперсии называют …
-: коэффициентом детерминации;
-: коэффициентом корреляции;
-: наблюдаемым значением критерия Стьюдента;
-: наблюдаемым значением критерия Фишера.
I: {3}, K=A;
S: Для множественной линейной регрессии значения скорректированного коэффициента детерминации _____ обычного коэффициента детерминации.
-: ближе к единице;
-: меньше;
-: больше;
-: равны.
I: {4}, K=A;
S:
Пусть исследуется
линейная зависимость вида
![]() и оценена регрессия
и оценена регрессия
![]() ,
,
![]() – фактические значения, а
– фактические значения, а
![]() –
расчетные значения зависимой переменной,
–
расчетные значения зависимой переменной,
![]() .
Тогда объясненную дисперсию можно
оценить по формуле …
.
Тогда объясненную дисперсию можно
оценить по формуле …
-:
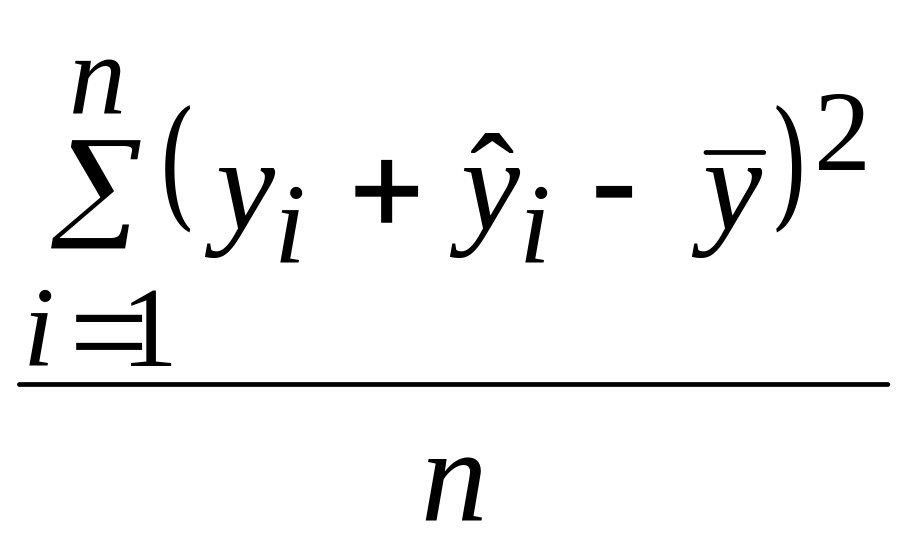 ;
;
-:
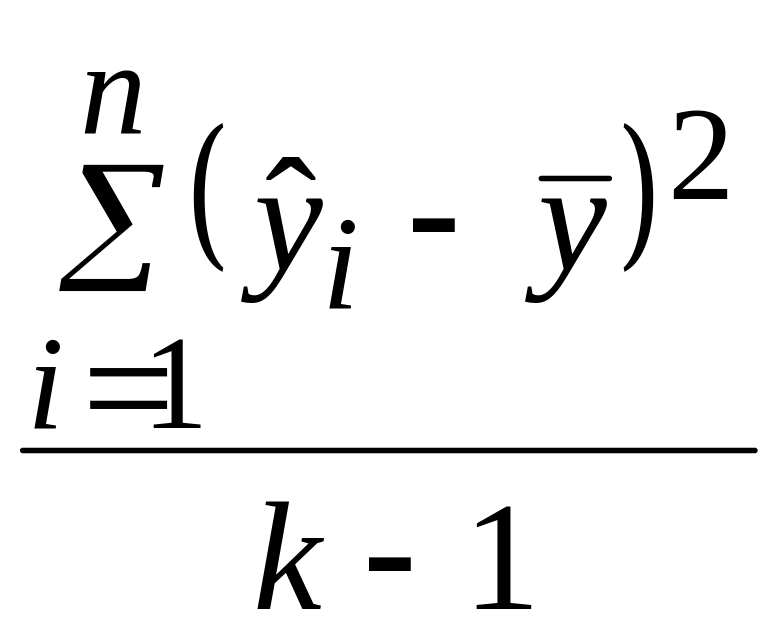 ;
;
-:
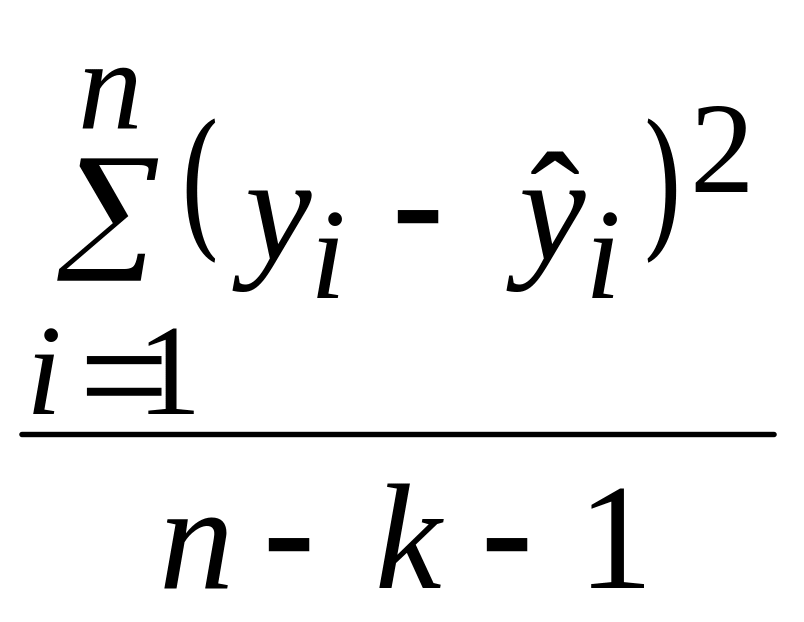 ;
;
-:
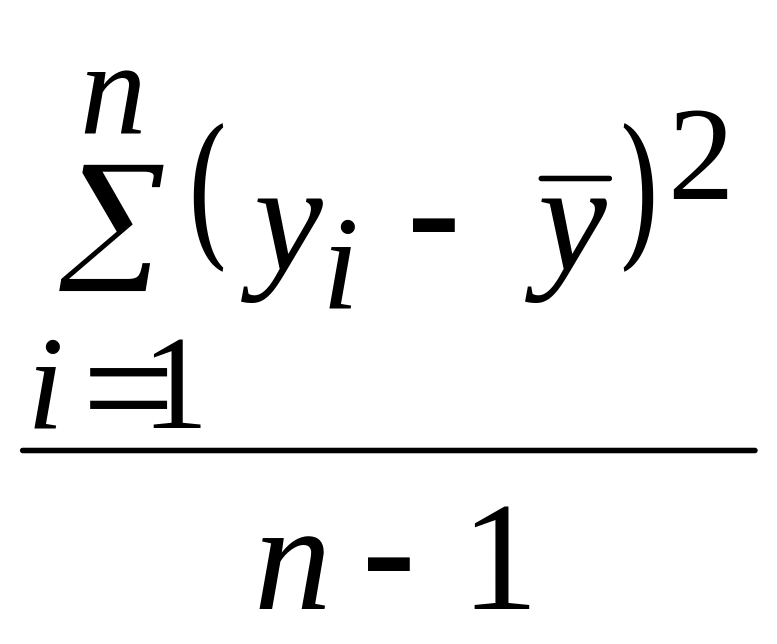 .
.
I: {5}, K=A;
S: Коэффициент детерминации равен нулю. Следовательно, сумма квадратов отклонений, объясненных регрессией равна …
-: 1;
-: 0;
-: -1;
-: 100 %.
V3:Проверка статистической значимости эконометрической модели
(Задание с выбором двух правильных ответов из предложенных)
I: {1}, K=A;
S: Выберите дисперсии, которые участвуют в расчете значения критерия Фишера.
-: независимая;
-: неопределенная;
-: остаточная;
-: факторная.
I: {2}, K=B;
S: Какие статистические гипотезы выдвигаются при проверке статистической значимости построенной модели?
-: нулевая о статистической незначимости;
-: зависимая о статистической зависимости;
-: альтернативная о статистической значимости;
-: независимая о статистической независимости.
I: {3}, K=A;
S: При проверке статистической значимости построенной модели проводят сравнение …
-: расчетного значения критерия Фишера;
-: альтернативного значения критерия Фишера;
-: табличного значения критерия Фишера;
-: нулевого значения критерия Фишера.
I: {4}, K=A;
S: В таблице представлены результаты дисперсионного анализа. Количество наблюдений, по которым построено уравнение регрессии, можно определить как ______ плюс 1.
Дисперсионный анализ |
Число степеней свободы |
Сумма квадратов |
Дисперсия на одну степень свободы |
F- критерий |
|
df |
SS |
MS |
F |
Регрессия |
3 |
300 |
100 |
10 |
Остаток |
10 |
100 |
10 |
|
Итого |
13 |
400 |
|
|
-: сумму чисел, определенных на пересечении столбца "df" и строк "Регрессия" и "Остаток";
-: "Остаток"-"Итого";
-: число на пересечении столбца "df" и строки "Регрессия";
-: число на пересечении столбца "df" и строки "Итого".
I: {5}, K=A;
S: В таблице представлены результаты дисперсионного анализа. Значение общей суммы квадратов можно определить, как …
Дисперсионный анализ |
Число степеней свободы |
Сумма квадратов |
Дисперсия на одну степень свободы |
F- критерий |
|
df |
SS |
MS |
F |
Регрессия |
3 |
300 |
100 |
10 |
Остаток |
10 |
100 |
10 |
|
Итого |
13 |
400 |
|
|
-: сумму чисел, определенных на пересечении столбца "SS" и строк "Регрессия" и "Остаток";
-: число на пересечении строки "Регрессия" и столбца "SS";
-: разность чисел, определенных на пересечении столбца "SS" и строк "Итого" и "Остаток";
-: число на пересечении строки "Итого" и столбца "SS".
V3: Оценка значимости параметров эконометрической модели
(Задание с выбором одного правильного ответа из предложенных)
I: {1}, K=A;
S: Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является…
-: нулевым;
-: существенным;
-: несущественным;
-: незначимым.
I: {2}, K=B;
S: Пусть
b
– оценка коэффициента регрессии, а
![]() – его стандартная ошибка. В принятых
обозначениях формула расчета t
– статистики для этого параметра
выглядит следующим образом:
– его стандартная ошибка. В принятых
обозначениях формула расчета t
– статистики для этого параметра
выглядит следующим образом:
-:
![]() ;
;
-:
![]() ;
;
-:
![]() ;
;
-:
![]() .
.
I: {3}, K=A;
S: Для уравнения регрессии выдвигается нулевая статистическая гипотеза о том, что b=0, которая используется для проверки существенности …
-: параметра a;
-: переменной y;
-: величины ;
-: . параметра b.
I: {4}, K=A;
S: Оценку существенности параметров регрессии можно назвать проверкой их …
-: неотрицательности;
-: монотонности;
-: значимого отличия от нуля;
-: равенства нулю.
I: {5}, K=A;
S: Для оценки статистической значимости коэффициента регрессии его величина сравнивается…
- : со стандартной ошибкой остатков;
-: с математическим ожиданием остатков;
-: с шириной его доверительного интервала;
-: с его стандартной ошибкой.
V3: Нелинейные зависимости в экономике
(Задание с выбором одного правильного ответа из предложенных)
I: {1}, K=A;
S: Известно, что с увеличением объема производства себестоимость единицы продукции уменьшается за счет того, что происходит перераспределение постоянных издержек. Пусть а – совокупная величина постоянных издержек, а b – величина переменных издержек в расчете на 1 изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели …
-:
![]() ;
;
-:
![]() ;
;
-:
![]() ;
;
-:
![]() .
.
I: {2}, K=B;
S: Если между экономическими показателями существует нелинейная связь, то …
-: нецелесообразно использовать спецификацию нелинейного уравнения регрессии;
-: необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии ;
-: целесообразно использовать линейное уравнение парной регрессии;
-: целесообразно использовать спецификацию нелинейного уравнения регрессии.
I: {3}, K=A;
S: Модель Филлипса служит для описания зависимости …
-: объема выпуска от затрат капитала и труда;
-: прибыли от расходов на рекламу;
-: спроса на товары различных групп от дохода;
-: уровня безработицы от изменения заработной платы.
I: {4}, K=A;
S:
Зависимость спроса на товары первой
необходимости от дохода (функция
Торнквиста,![]()
![]() )
характеризуется обратной эконометрической
моделью с начальным уровнем
)
характеризуется обратной эконометрической
моделью с начальным уровнем
![]() вида …
вида …
-:
![]() ;
;
-:
![]() ;
;
-:
![]() ;
;
-:
![]() .
.
I: {5}, K=A;
S:
Кривая Филипса, характеризует соотношение
между нормой безработных (![]() )
и процентом прироста заработной платы
(
)
и процентом прироста заработной платы
(![]() )
)
![]() и является _____ функцией с _______ горизонтальной
асимптотой
и является _____ функцией с _______ горизонтальной
асимптотой
![]() .
.
-: убывающей … нижней;
-: возрастающей … верхней;
-: убывающей … верхней;
-: возрастающей … нижней.
V3: Нелинейные модели регрессии
(Задание с выбором одного правильного ответа из предложенных)
I: {1}, K=A;
S: В зависимости от типа взаимосвязи между независимой переменной и регрессором, регрессионные модели подразделяются на …
-: парные и множественные;
-: линейные и нелинейные;
-: скалярные и векторные;
-: нет правильного ответа.
I: {2}, K=A;
S: В зависимости от количества регрессоров, модели подразделяются на …
-: стационарные и нестационарные;
-: статические и динамические;
-: парные и множественные;
-: линейные и нелинейные.
I: {3}, K=A;
S: Независимые переменные в регрессионных моделях называются …
-: остатками;
-: откликами;
-: регрессорами;
-: возмущениями.
I: {4}, K=A;
S: Оценка случайного возмущения по выборочным данным называется …
-: откликом;
-: остатком;
-: регрессором;
-: нет правильного ответа.
I: {5}, K=A;
S:
К какому классу
нелинейности относится модель
![]() ?
?
-: регрессия, имеющая линейный вид;
-: регрессия, нелинейная по оцениваемым параметрам;
-: регрессия, имеющая полиномиальный вид;
-: нет правильного ответа.
I: {6}, K=A;
S: Какой из тестов используют для выбора формы модели?
-: тест Рамсея;
-: тест Дарбина-Уотсона;
-: тест Бокса-Кокса;
-: нет правильного ответа.
I: {7}, K=A;
S: В зависимости от количества регрессоров, модели подразделяются на …
-: парные и множественные;
-: стационарные и нестационарные;
-: скалярные и векторные;
-: линейные и нелинейные.
V3: Коэффициент эластичности
(Задание с выбором одного правильного ответа из предложенных)
I: {1}, K=A;
S: Какой коэффициент указывает в среднем процент изменения результативного показателя Y при увеличении аргумента X на 1%?
-: бета-коэффициент;
-: коэффициент детерминации;
-: коэффициент эластичности;
-: коэффициент регрессии.
I: {2}, K=C;
S:
Приведенная формула
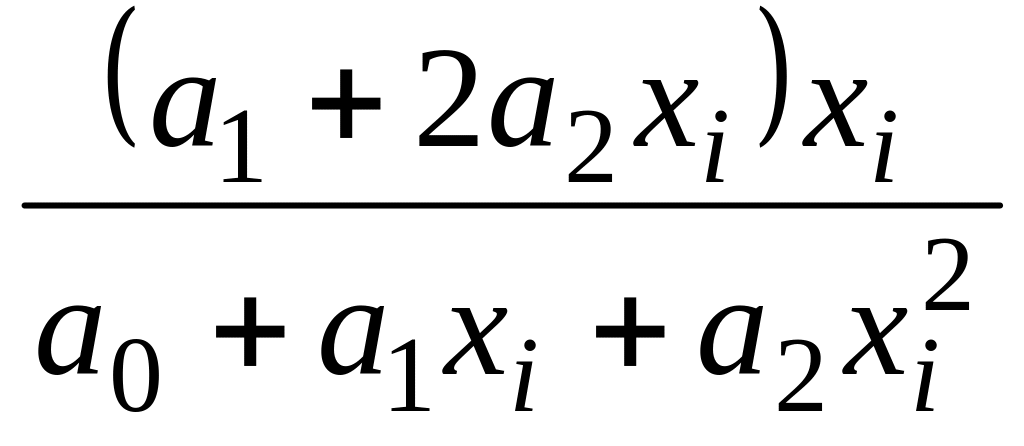 предназначена
для расчета коэффициента эластичности
…
предназначена
для расчета коэффициента эластичности
…
-: в случае параболы второго порядка;
-: в случае прямой;
-: в случае гиперболы;
-: нет правильного ответа.
I: {3}, K=C;
S:
Приведенная формула
![]() предназначена
для расчета коэффициента эластичности
…
предназначена
для расчета коэффициента эластичности
…
-: в случае параболы второго порядка;
-: в случае прямой;
-: в случае гиперболы;
-: нет правильного ответа.
I: {4}, K=B;
S:
Приведенная формула
![]() предназначена
для расчета коэффициента эластичности
…
предназначена
для расчета коэффициента эластичности
…
-: в случае параболы второго порядка;
-: в случае прямой;
-: в случае гиперболы;
-: нет правильного ответа.
F1: Эконометрика
F2: Тамбовский государственный технический университет
F3: Тесты для пробного тестирования
