
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Замечательные пределы
no1. Первый замечательный предел и его следствия.
Покажем,
что
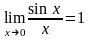 (1)(первый
замечательный предел), т.е., что
(1)(первый
замечательный предел), т.е., что
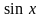 ~
(
~
(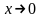 ).
).
Так
как функция
 – четная, то достаточно найти правосторонний
ее предел в точке
– четная, то достаточно найти правосторонний
ее предел в точке
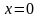 .
Пусть
.
Пусть
 .
Тогда как видно из следующего рисунка
.
Тогда как видно из следующего рисунка
 ,
,
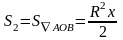 ,
,
 ,
при этом ясно, что
,
при этом ясно, что
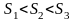 .
Поэтому
.
Поэтому
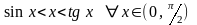 (2)
и, следовательно,
(2)
и, следовательно,
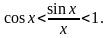 Таким
образом, если будет доказано, что
Таким
образом, если будет доказано, что
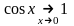 (3), то будет доказано и (1).
(3), то будет доказано и (1).
Используя
левое из неравенств (2) получим
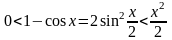 (4), а так как
(4), а так как
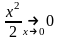 ,
то из этих неравенств в силу принципа
двух милиционеров получим (3). а
следовательно и (1).
,
то из этих неравенств в силу принципа
двух милиционеров получим (3). а
следовательно и (1).
Как
следствие (1) и (3) имеем
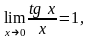 (5).
В свою очередь из (1) и (4) следует что
(5).
В свою очередь из (1) и (4) следует что
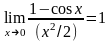 (6) Таким образом,
(6) Таким образом,
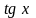 ~
,
а
~
,
а
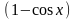 ~
~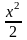 при
.
при
.
no2. Второй замечательный предел
Имеет
место равенство
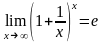 (7).
Покажем
сначала, что
(7).
Покажем
сначала, что
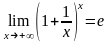 (8)
(8)
Действительно,
так как
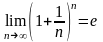 ,
то для
любой последовательности натуральных
чисел
,
то для
любой последовательности натуральных
чисел
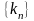 такой,
что
такой,
что
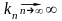 имеем
имеем
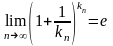 (9)
(9)
Но
для любой последовательности вещественных
чисел
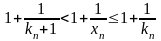 ,
где
,
где
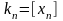 ,
и, следовательно,
,
и, следовательно,
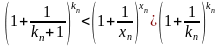 .
.
Поэтому,
если
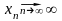 ,
то
,
то
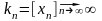 и в силу (9) и принципа двух милиционеров,
для любой последовательности вещественных
чисел
,
такой, что
имеем также
и в силу (9) и принципа двух милиционеров,
для любой последовательности вещественных
чисел
,
такой, что
имеем также
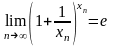 .
.
По
определению предела в смысле Гейне это
и означает, что справедливо равенство
(8). Используя его и теорему о пределе
суперпозиции легко убедиться также и
в том, что
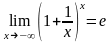 (10). Наконец (7) следует из (8) и (10).
(10). Наконец (7) следует из (8) и (10).
Асимптоты графика функции
Определение1.
Прямая
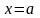 называется вертикальной
асимптотой
графика
функции
,
если хотя бы один из пределов
называется вертикальной
асимптотой
графика
функции
,
если хотя бы один из пределов
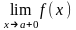 или
или
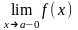 равен
или
равен
или
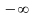 .
.
Определение
2. Прямая
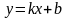 называется наклонной
асимптотой графика
функции
при
называется наклонной
асимптотой графика
функции
при
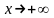 (
( ),
если
),
если
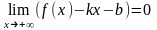 (
(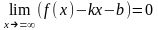 ).
(1)
).
(1)
Теорема.
Для того,
чтобы прямая
была наклонной
асимптотой графика функции
при
(
),
необходимо и достаточно, чтобы
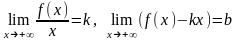 (
(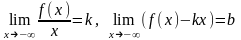 ).
(2)
).
(2)
Д
о к а з а т е л ь с т в о . Пусть, например,
- наклонная асимптота графика функции
при
.
Тогда из равенств
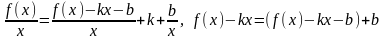 в силу (1) следует (2). Необходимость
доказана.
в силу (1) следует (2). Необходимость
доказана.
Докажем достаточность. Действительно, если имеют равенства (2), то из второго из них следует (1), т.е. - наклонная асимптота графика функции при □
Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
Определение
1. Функция
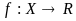 ,
,
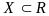 ,
называется непрерывной
в точке
,
называется непрерывной
в точке
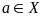 ,
если для любого
,
если для любого
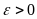 существует такое
существует такое
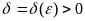 ,
что для любого
,
что для любого
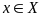 ,
удовлетворяющего неравенству
,
удовлетворяющего неравенству
 (1), справедливо также и неравенство
(1), справедливо также и неравенство
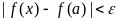 (2).
(2).
Замечание
1. Данное
определение иногда называется определением
непрерывности функции на языке
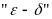 .
По форме оно явно напоминает определение
предела функции в форме Коши, при этом
в отличие от него здесь требуется, чтобы
точка
.
По форме оно явно напоминает определение
предела функции в форме Коши, при этом
в отличие от него здесь требуется, чтобы
точка
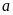 принадлежала множеству
,
но не требуется, чтобы она была точкой
сгущения этого множества.
принадлежала множеству
,
но не требуется, чтобы она была точкой
сгущения этого множества.
В
связи с последним замечанием отметим,
что если точка
не является точкой сгущения множества
,
то она называется изолированной
точкой этого множества. Иными словами
точка
называется изолированной точкой
множества
,
если существует такая ее окрестность
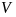 ,
что
,
что
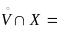 Æ
или, что тоже самое,
Æ
или, что тоже самое,
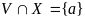 .
.
Замечание
2. Согласно
определению 1 в любой изолированной
точке своей области определения всякая
функция является непрерывной.
Действительно, каково бы ни было
по определению изолированной точки
можно выбрать столь малое
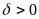 ,
что
,
что
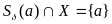 и, следовательно, при этом
среди точек множества
неравенству (1) будет удовлетворять
только точка
,
но при
и, следовательно, при этом
среди точек множества
неравенству (1) будет удовлетворять
только точка
,
но при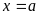 неравенство (2), очевидно, выполняется
для любой функции
неравенство (2), очевидно, выполняется
для любой функции
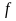 .
.
Замечание
3. В силу
того, что для
неравенство (2) выполняется очевидным
образом, можно заключить, что в том
случае, когда точка
является точкой сгущения множества
,
неравенство (1) можно заменить неравенствами:
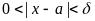 (т.е. точку
можно исключить из рассмотрения), при
этом определение 1 превратится в
определение предела
(т.е. точку
можно исключить из рассмотрения), при
этом определение 1 превратится в
определение предела
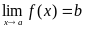 при
при
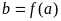 .
.
Таким
образом, можно сказать, что если точка
является точкой сгущения множества
,
то функция
непрерывна в этой точке в том и только
том случае, когда
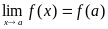 .
.
Замечание 4. На языке окрестностей определение 1 можно переформулировать следующим образом:
Определение
1’. Функция
,
,
называется непрерывной в точке
,
если для любого
существует такое
,
что
 (т.е.
(т.е.
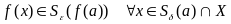 ).
).
Это определение, а значит и определение 1, очевидно равносильно следующему определению:
Определение
1”. Функция
,
,
называется непрерывной в точке
,
если для любой окрестности
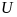 точки
существует такая окрестность
точки
,
что
точки
существует такая окрестность
точки
,
что
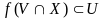 .
.
С
учетом замечаний 2 и 3, теоремы о
равносильности определений предела по
Коши и по Гейне, а также с учетом того,
что всякую точку
можно представить в виде

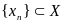 ,
заключаем, что определения 1, 1’и 1"
равносильны следующему определению на
языке последовательностей:
,
заключаем, что определения 1, 1’и 1"
равносильны следующему определению на
языке последовательностей:
Определение
2. Функция
,
,
называется непрерывной в точке
,
если для любой последовательности точек
,
 ,
последовательность
,
последовательность
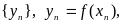 сходится и ее предел равен значению
функции
в
точке
:
сходится и ее предел равен значению
функции
в
точке
:
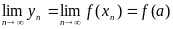 .
.
Упражнение 1. Докажите формально равносильность определений 1 и 2.
Как будет показано каждая элементарная функция является непрерывной в своей области определения, т.е. непрерывной в любой точке своей области определения. В связи с этим напомним, что к числу, так называемых, основных элементарных функций относятся:
–
постоянная
функция:
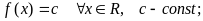
–
степенная
функция:
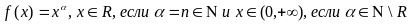 ;
;
–
показательная
функция:
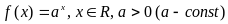 ;
;
–
логарифмическая
функция:
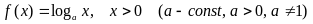 ;
;
–
тригонометрические
функции:
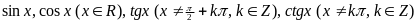 ;
;
–
обратные
тригонометрические функции:
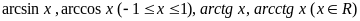 .
.
В свою очередь, элементарной называется всякая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций и образования суперпозиций.
Теорема
1 (О непрерывности
сужения).
Пусть функция
 непрерывна в точке
непрерывна в точке
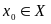 и
и
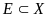 причем
причем
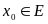 .
Тогда функция
.
Тогда функция
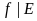 также непрерывна в точке
также непрерывна в точке
 .
.
Д о к а з а т е л ь с т в о непосредственно вытекает из определения сужения и определения непрерывности.
Отметим еще ряд теорем, которые с учетом замечаний 2 и 3 вытекают из аналогичных теорем о пределе функции.
Теорема
2 (Арифметические
свойства непрерывных функций).
Пусть
функции
и
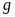 определены на множестве
определены на множестве
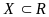 и непрерывны в точке
.
Тогда и функции:
и непрерывны в точке
.
Тогда и функции: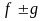 ,
,
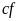
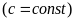 ,
,
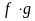 ,
,
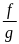 (при
(при
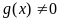 на
на
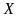 )
непрерывны в точке
.
)
непрерывны в точке
.
Теорема
3 (О локальной
ограниченности).
Пусть функция
определена на множестве
и непрерывна в точке
.
Тогда если
–
точка сгущения множества
,
то существует такая окрестность
точки
,
что функция
ограничена на множестве
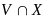 .
.
Теорема
4 (О стабилизации
знака).
Пусть функция
определена на множестве
и непрерывна в точке
.
Тогда если
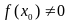 и
–
точка сгущения множества
,
то существует такая окрестность
и
–
точка сгущения множества
,
то существует такая окрестность
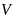 точки
,
что
точки
,
что
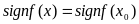
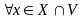 .
.
Наконец отметим еще две простые теоремы
Теорема
5. Пусть
функция
определена на множестве
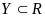 и непрерывна в точке
и непрерывна в точке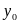 ,
а функция
определена
на множестве
и непрерывна в точке
,
а функция
определена
на множестве
и непрерывна в точке
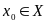 ,
причем
,
причем
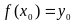 и
и
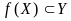 .
Тогда сложная функция
.
Тогда сложная функция
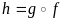 непрерывна в точке
.
непрерывна в точке
.
Д
о к а з а т е л ь с т в о. Выберем произвольную
последовательность
,
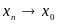 .
Так как
- непрерывна в точке
,
то
.
Так как
- непрерывна в точке
,
то
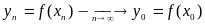 ,
а так как
,
то
,
а так как
,
то
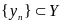 .
Поэтому, в силу непрерывности функции
в точке
.
Поэтому, в силу непрерывности функции
в точке
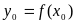 ,
имеем
,
имеем
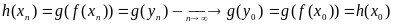 ,
то есть
,
то есть
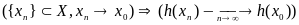 ,
что и означает, что функция
,
что и означает, что функция
 - непрерывна в точке
- непрерывна в точке
Пусть
функция
определена на множестве
и
 .
Рассмотрим множества:
.
Рассмотрим множества: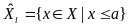 ,
,
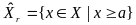 .
.
Определение
1. Функция
называется непрерывной
слева
(непрерывной
справа) в
точке
,
если в ней непрерывна функция
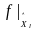 (соответственно,
(соответственно,
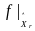 )
.
)
.
Замечание.
На языке
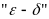 , например, определение непрерывности
слева, формулируется следующим образом:
функция
называется непрерывной слева в точке
,
если
, например, определение непрерывности
слева, формулируется следующим образом:
функция
называется непрерывной слева в точке
,
если
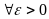
 такое, что
такое, что
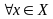 удовлетворяющего неравенствам
удовлетворяющего неравенствам
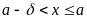 справедливо неравенство
.
справедливо неравенство
.
Теорема
6. Функция
непрерывна в точке
 она непрерывна в ней слева и справа
одновременно.
она непрерывна в ней слева и справа
одновременно.
Если - изолированная точка множества , то утверждение очевидно. Если же - точка сгущения множества , то оно вытекает из аналогичной теоремы об односторонних пределах.
