
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Бесконечно малые и бесконечно большие последовательности.
Последовательность
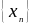 называется бесконечно
малой (б.м.),
если
называется бесконечно
малой (б.м.),
если
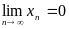 .
.
Замечание
1. Очевидно,
что если
 ,
то
,
то
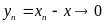 ,
(т.е.
,
(т.е.
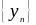 -
б. м. последовательность)
при этом
-
б. м. последовательность)
при этом
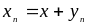 .
.
Наоборот, если имеет место это равенство и - б. м. последовательность, то .
Таким образом, последовательность имеет предел тогда и только тогда, когда она равна сумме постоянной и бесконечно малой последовательностей.
Теорема 1. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
Определение
2. Если для
любого вещественного числа E
N:
xn
> E
n
> N
(соотв., xn
< E
n
> N
),
то говорят, что последовательность
имеет своим пределом
 ,
и пишут
,
и пишут
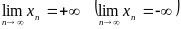 или
или
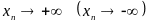 .
.
Определение
3.
Последовательность
такую, что
 ,
называют бесконечно
большой
и пишут
,
называют бесконечно
большой
и пишут
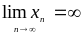 (символ
употребляется без знака).
(символ
употребляется без знака).
Теорема
2. Если
последовательность
- бесконечно большая и
 то
то
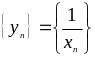 - бесконечно
малая последовательность.
- бесконечно
малая последовательность.
Теорема
3. Если
- бесконечно
малая последовательность и
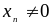 при n
= 1,2,…,
то
последовательность
при n
= 1,2,…,
то
последовательность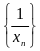 -бесконечно
большая.
-бесконечно
большая.
Замечание 2. Последовательности, имеющие своим пределом + или - мы не относим к сходящимся, то есть они считаются расходящимися. Таким образом, можно сказать, что сходящиеся последовательности – это такие последовательности, которые имеют конечный предел.
Замечание
3.
Последовательности, имеющие пределы
+
или -,
очевидно, являются бесконечно большими.
Однако не всякая бесконечно большая
последовательность имеет предел равный
+
или -.
Например, последовательность
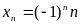 очевидно
является бесконечно большой (
очевидно
является бесконечно большой ( ),
но она не имеет ни конечного, ни какого-то
бесконечного ()
предела.
),
но она не имеет ни конечного, ни какого-то
бесконечного ()
предела.
Лемма о вложенных отрезках.
Лемма.
Для любой последовательности вложенных
отрезков
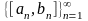 ,
,
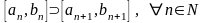 (
(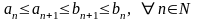 ),
их пересечение
),
их пересечение
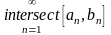 не пусто.
не пусто.
Более
того, если длины
 этих отрезков стремятся к нулю
этих отрезков стремятся к нулю
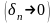 ,
то это пересечение состоит из одной
точки.
,
то это пересечение состоит из одной
точки.
Доказательство. Из определения о вложенных отрезках.
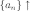 ,
что для любого
,
что для любого  ,
следовательно, существует
,
следовательно, существует 
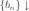 ,
что для любого
,
что для любого 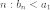 ,
и существует
,
и существует 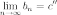
Так
как мы доказываем единственность точки,
следовательно, пределы последовательностей
в этой точке  и
и 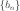 равны.
Из этого следует,
равны.
Из этого следует, 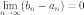
Как
нам известно
,
а
,
то

Что и требовалось доказать.
Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
Пусть
– произвольная числовая последовательность,
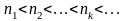 – возрастающая последовательность
натуральных чисел. Тогда последовательность
– возрастающая последовательность
натуральных чисел. Тогда последовательность
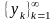 ,
,
 ,
,
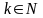 ,
называется подпоследовательностью
последовательности
и обычно обозначается
,
называется подпоследовательностью
последовательности
и обычно обозначается
 или, короче,
или, короче,
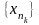 .
.
Теорема 1. Всякая подпоследовательность сходящейся последовательности сходится и имеет тот же предел, что и исходная последовательность.
Теорема 2 (Больцано-Вейерштрасса). Всякая ограниченная последовательность содержит сходящуюся подпоследовательность.
Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.
Замечание 1. Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.
В самом деле, в силу теоремы Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.
Замечание
2. Пусть {xn}
- ограниченная последовательность,
элементы которой находятся в сегменте
[a, b].
Тогда предел с любой сходящейся
подпоследовательности 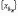 также
находится на сегменте [a, b].
также
находится на сегменте [a, b].
Действительно,
так как 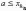
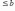 ,
то в силу следствия
2 выполняются
неравенства a ≤ c ≤ b.
Это и означает, что c находится
на сегменте [a, b].
,
то в силу следствия
2 выполняются
неравенства a ≤ c ≤ b.
Это и означает, что c находится
на сегменте [a, b].
Отметим, что в отдельных случаях и из неограниченной последовательности также можно выделить сходящуюся подпоследовательность. Например, последовательность 1, 1/2, 2, 1/3, ..., n, 1/(n+1), ... неограниченная, однако подпоследовательность 1/2, 1/3, ..., 1/n, ... ее элементов с четными номерами сходится. Но не из каждой неограниченной последовательности можно выделить сходящуюся подпоследовательность. Например, любая подпоследовательность неограниченной последовательности 1, 2, ..., n, ... расходится. Поэтому теорему Больцано-Вейерштрасса, вообще говоря, нельзя распространить на неограниченные последовательности.
