
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
Число
(точка)
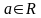 называется пределом
последовательности
называется пределом
последовательности
 ,
если для любого
,
если для любого
 существует такой номер
существует такой номер
 ,
что для всех натуральных
,
что для всех натуральных
 имеет место неравенство
имеет место неравенство
 .
.
(Обозначение:
 ,
или
,
или
 (а также
(а также
 при
при
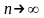 ))
))
Краткое,
символическое определение:

Геометрическая форма определения предела последовательности:
Интервал
 =
=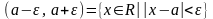 называется
называется
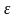 -окрестностью
точки
-окрестностью
точки
 .
.
Так
как


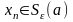
То

Наконец,
определение предела числовой
последовательности может быть
сформулировано следующим образом: Число
(точка)
называется пределом
последовательности
,
если все ее члены, начиная с некоторого
номера, принадлежат любой наперед
заданной окрестности
 точки
.
точки
.
Если числовая последовательность имеет предел, то говорят, что она сходится и называют ее сходящейся. В противном случае, т.е. если она не имеет предела, говорят, что она расходится и называют ее расходящейся.
(Очевидно, что если последовательность сходится (расходится), то сходящейся (расходящейся) будет и последовательность полученная из нее добавлением или исключением из нее конечного числа членов, при этом в случае сходимости исходной последовательности новая последовательность, будет иметь тот же предел, что и исходная. )
Единственность предела.
Всякая сходящаяся последовательность имеет только один предел.
Числовая
последовательность
 называется
называется
А)
ограниченной,
если
 :
:


Б)
ограниченной
сверху, если
 :
:

В)
ограниченной
снизу, если
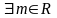
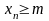
Всякая сходящаяся последовательность ограничена.
(Утверждение обратное к утверждению последней теоремы, вообще говоря, неверно.)
Пример
1. Рассмотрим
последовательность
такую, что
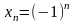 ,
,
 . Эта последовательность представляет
собой чередующиеся числа
. Эта последовательность представляет
собой чередующиеся числа
 :
:
 .
.
Очевидно,
она ограничена
Но
если
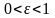 ,
то каково бы ни было
числа
одновременно не могут принадлежать
-окрестности
,
то каково бы ни было
числа
одновременно не могут принадлежать
-окрестности
 ,
так как расстояние между точками
,
так как расстояние между точками
 и
и
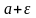 равно
равно
и при меньше двух, а расстояние между двумя соседними точками рассматриваемой последовательности равно двум и следовательно они одновременно не могут принадлежать такой -окрестности любой точки .
Пример
(стационарные
последовательности).
Последовательность
называется стационарной
, если все
ее члены за исключением быть может
конечного их числа равны одному и тому
же вещественному числу
, т.е. если
 такое, что
такое, что
 .
.
Очевидно, всякая стационарная последовательность сходится и ее предел равен тому числу , которому равны все ее члены за исключением конечного их числа.
Очевидно,
для любого вещественного числа
существует единственное целое число
 такое,
что
такое,
что
 .
.
Оно
называется целой
частью числа
и обычно обозначается
 .
.
Арифметические свойства сходящихся последовательностей.
Суммой,
разностью, произведением и частным
последовательностей
и
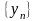 называются, соответственно, следующие
последовательности:
называются, соответственно, следующие
последовательности:
 ,
,
 ,
,
 и
и
 ,
при этом, говоря о последней из них,
предполагается, что
,
при этом, говоря о последней из них,
предполагается, что
 для любого
для любого
 .
.
Теорема 1. ⊐ последовательности и сходятся.
Тогда
сходятся и последовательности
 (c-
const),
(c-
const),
 ,
и
–
последняя при условии
,
и
–
последняя при условии
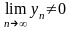 и
и
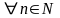 ,
– при этом
,
– при этом
а)
 ,
,
б)
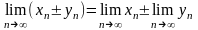 (теорема о пределе суммы и разности)
(теорема о пределе суммы и разности)
в)
 (теорема о пределе произведения)
(теорема о пределе произведения)
г)
 (теорема о пределе частного)
(теорема о пределе частного)
