51. Комплексные числа.

Определение 1. Комплексными числами называются всевозможные упорядоченные пары 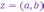вещественных чисел и 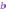, при этом для этих пар понятия равенства, суммы, произведения и отождествления некоторых пар с вещественными числами вводятся по следующим правилам (аксиомам):

I. 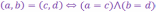(равенство к.ч.)

II. (сумма к.ч)

III. 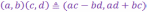(произведение к.ч.)

IV. 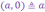(отождествление некоторых к.ч с в.ч.)

Множество всех комплексных чисел обозначается буквой .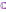

Свойства операций сложения и умножения к.ч.

Легко проверить, что операции сложения коммутативна: 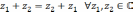и ассоциативна: .

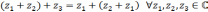Комплексное и, в соответствии с IV, одновременно вещественное число 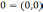очевидно обладает тем свойством, что

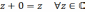
Комплексное числ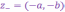о называется противоположным к.ч. , при этом очевидно 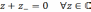. Нетрудно убедиться, что операция умножения комплексных чисел коммутативна: , ассоциативна: , дистрибутивна по отношению к сложению:

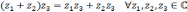
Отметим, что для любого к.ч. в соответствии с определением операции умножения и, следовательно пара 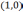играет роль единицы при умножении к.ч., что согласуется с тем, что комплексное число отождествляется с вещественным числом 1.

Вообще отметим, что в соответствии с аксиомами III и IV

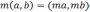
Действительно,

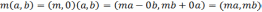
Вычитание и деление к.ч.

Разность к.ч. вводится на основе операции сложения и понятия противоположного к.ч. по следующему правилу:

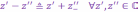
Пусть к.ч. отлично от нуля, т.е. отлично от нуля хотя бы одно из вещественных чисел 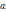и 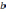. Тогда к.ч. 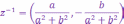называется обратным к к.ч. .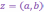

Очевидно, .

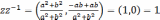Операция деления к.ч. вводится на основе операции умножения и введенного выше понятия обратного к.ч. А именно, частным от деления к.ч. на к.ч. 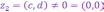называется к.ч.

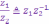
Замечание1. Нетрудно показать, что при умножении числителя и знаменателя дроби 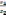на одно и то же к.ч. 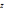она не изменится, т.е

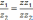
Комплексное число 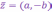называется комплексно сопряженным к (для) к.ч. .

Ясно, что к.ч. , в свою очередь, является комплексно сопряженным к к.ч. 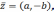т.е. комплексно сопряженное к комплексно сопряженному для к.ч. 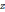есть само к.ч. .

Для любой пары комплексно сопряженных чисел и 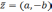, очевидно, + .

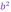Действительно, +

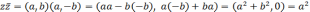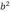
Таким образом, произведение 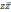к.ч. на ему комплексно сопряженное является вещественным числом.

n^o2. Алгебраическая форма к.ч.

К.ч. 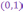называется мнимой единицей и обозначается буквой .

Таким образом, 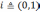. По определению умножения к.ч. имеем

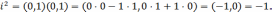
Следовательно,

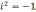
Для любого комплексного числа , очевидно, что (здесь нужно учесть, что 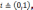а по аксиоме IV ).

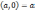Запись к.ч. в виде 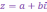называется алгебраической формой записи этого к.ч. , при этом вещественное число называют вещественной частью к.ч. и обозначают , а в.ч. 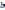называют его мнимой частью и обозначают (

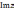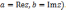
Ясно, что число, комплексно сопряженное к к.ч. 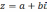в алгебраической форме записи имеет вид 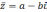, а операции сложения, умножения, вычитания и деления при использовании алгебраической форме записи к.ч. производятся по формулам:

,

,

,

.

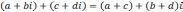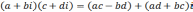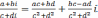n^o3.Тригонометрическая форма к.ч.

Пусть на плоскости введена декартова прямоугольная система координат 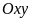. Тогда каждому к.ч. можно сопоставить точку на этой плоскости с координатами и по осям 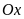и 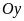, соответственно. При этом каждому к.ч. соответствует точка на этой плоскости, а каждой точке на ней - определенное к.ч.

Таким образом, к.ч. соответствует точка 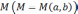. Длину ее радиус-вектора обозначим , ,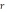

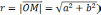Предполагая, что 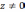(т.е., что угол между радиус-вектором и положительным направлением оси , отсчитываемым от нее против часовой стрелки, обозначим через 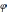. Тогда для координат точки 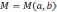будем иметь формулы и, следовательно, к.ч. можно записать в виде .

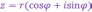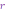Такая форма записи к.ч. называется тригонометрической формой записи этого к.ч., при этом (заведомо неотрицательное) вещественное число называют модулем к.ч. и обозначают 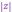, а число 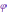называют аргументом к.ч. и обозначают .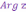

Модуль к.ч. определяется однозначно, 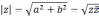, а аргумент 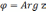, - с точностью до слагаемого, кратного 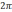, исходя из уравнений .

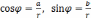Подчеркнем здесь еще раз, что аргумент не определен для к.ч. .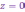

Умножение комплексных чисел в тригонометрической форме записи.

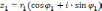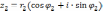Пусть и . Тогда

(1)

Таким образом, 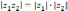, (2), 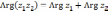, (3) т.е. при умножении к.ч. их модули перемножаются, а аргументы складываются (модуль произведения равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей).

Исходя из формулы (1) индукцией по легко устанавливается, что для любых к.ч. 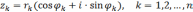имеет место формула

(4)

а следовательно имеют место и формулы

,

(5)

и

,

(6)

n^o4.Извлечение корня 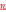-ой степени из комплексного числа.

Положим в (4) , 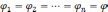. получим формулу -ой степени к.ч.

.

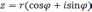
(7)

При 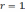отсюда следует формула Муавра:

.

(8)

Предыдущую формулу (7) также иногда называют формулой Муавра.

Нетрудно убедиться, что формула Муавра (8) справедлива не только для целых положительных , но и при неположительных целых .

Определение 1. Пусть - натуральное число. Корнем -ой степени из к.ч. называется к.ч. такое, что .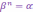

Корень -ой степени из к.ч.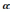 обозначается .

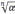Найдем все корни -ой степени из к.ч. . Если 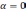, то единственным значением является число 0. Поэтому пусть 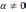. Запишем 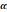в тригонометрической форме 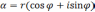и будем искать 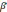также в тригонометрической форме .

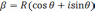С учетом формулы (7) запишем равенство 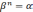в виде .

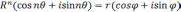Но данное равенство равносильно следующим равенствам: 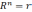, и 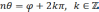, (здесь учитывается многозначность аргумента к.ч.).

Следовательно, 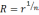, а

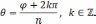
Таким образом, всевозможные корни -ой степени из к.ч. даются формулой

(9)

Более того, оказывается, что при 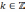в этой формуле многие корни повторяются бесконечно много раз. Вместе с тем справедлива следующая\

Теорема. Существует ровно различных значений корня -ой степени из отличного от нуля к.ч. . Их дает формула (9) при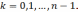
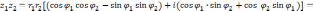
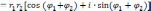
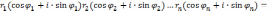
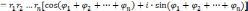
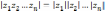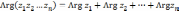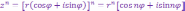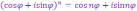