49. Точки перегиба графика функции.

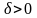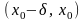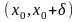Определение 2. Пусть функция определена и дифференцируема в некоторой окрестности точки . Если существует такое , что на интервалах и функция имеет разные направления выпуклости, т.е. на одном из них она выпукла, а на другом, напротив, вогнута, то точка ее графика называется точкой перегиба.

Таким образом, можно сказать, что при переходе через точку перегиба график функции как бы переходит с одной стороны касательной в этой точке на другую ее сторону.

Если точка является точкой перегиба графика дважды дифференцируемой в точке функции , то в соответствии с определением 2 и теоремой 1, а также ее аналогом для вогнутых функций, точка – точка локального экстремума производной и поэтому по теореме Ферма .

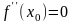Таким образом, условие (10) является необходимым для того, чтобы точка была точкой перегиба графика дважды дифференцируемой функции .

В свою очередь, в силу определения 3 и следствия из теоремы 2 , а также его аналога для вогнутых функций, если на некотором интервале слева от точки вторая производная 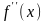имеет один знак, а на соответствующем интервале справа от этой точки она имеет другой знак, то этого достаточно для того, чтобы точка была точкой перегиба.

50. Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.

–множество всех натуральных чисел ( N = {1, 2, 3, . . . } );

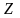– множество всех целых чисел ( = {0, ±1, ±2, ±3, . . . } );

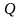– множество всех рациональных чисел, Q = { x | x = p/q, р Z, q N };

– множества всех вещественных чисел.

Множество вещественных чисел далее иногда будет называться полем вещественных чисел.

Говоря о вещественных числах напомним, что множество вещественных чисел состоит из всех рациональных чисел и из всех иррациональных чисел. Каждое рациональное число можно записать либо в виде конечной десятичной дроби 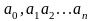(здесь – целое, а 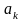для любого 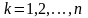равно одному из чисел 0, 1, 2, …,9), либо в виде периодической бесконечной десятичной дроби 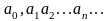; каждое иррациональное вещественное число отождествляется с бесконечной непериодической десятичной дробью. Таким образом, можно сказать, что множество вещественных чисел это – множество всех десятичных дробей (как конечных, так и бесконечных).

Во множестве вещественных чисел вводятся алгебраические операции сложения и умножения, а также обратные к ним операции вычитания и деления, соответственно.

Между множеством вещественных чисел и точками той или иной прямой можно установить взаимно-однозначное соответствие и, следовательно, множество вещественных чисел можно отождествить с прямой (поэтому оно часто называется числовой прямой).

Между любыми двумя различными вещественными числами лежит по крайней мере одно рациональное число (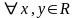 таких, что , : ).

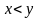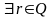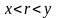Понятие абсолютной величины (или модуля) 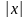вещественного числа и ее свойства.

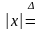
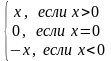
Свойства модуля в.ч.

1^о > 0 .

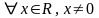2^o

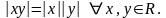
3^o .

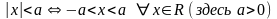4^o .

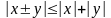5^о .

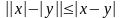Множество вещественных чисел дополненное элементами и называется расширенным множеством вещественных чисел или расширенной числовой прямой и обозначается 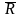(т.о. ).
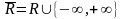