48. Условия выпуклости функции.

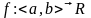
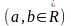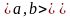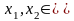Определение 1. Функция называется выпуклой (соотв., вогнутой) на промежутке , если для любых и любых 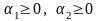таких, что 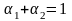имеет место неравенство: 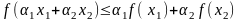(соотв., ). (1)

При этом, если это неравенство является строгим при и 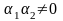, то функция называется строго выпуклой (строго вогнутой).

Замечание 1. В этом определении без ущерба для общности можно считать, что 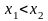и . Эти неравенства далее предполагаются выполненными.

Замечание 2. Геометрически условие (1) означает, что любая дуга графика функции лежит под хордой, стягивающей эту дугу (см. рис.1)

Рис.1

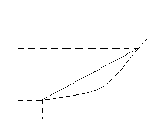
Аналогичное условие вогнутости функции означает, соответственно, что любая дуга графика функции лежит над хордой, стягивающей эту дугу.

Замечание 3. Очевидно, фунуция является вогнутой в том и только том случае, когда функция 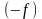является выпуклой. Поэтому далее мы ограничимся изучением только выпуклых функций, при этом утверждения, устанавливаемые ниже для выпуклых функций, читателю предлагается самостоятельно переформулировать для вогнутых функций.

Лемма 1. Для того, чтобы функция была выпуклой (строго выпуклой) на промежутке необходимо и достаточно, чтобы для любых таких, что 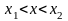, выполнялось неравенство 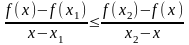(соответственно, 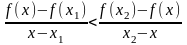) (2)

Д о к а з а т е л ь с т в о опускаем.

Теорема 1 (критерий выпуклости функции в терминах первой производной)

Для того, чтобы дифференцируемая на интервале функция была выпуклой (строго выпуклой) на нем необходимо и достаточно, чтобы её производная была неубывающей (соответственно, возрастающей) на интервале функцией.

Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)

Действительно, в силу леммы 1 имеем . Устремляя здесь сначала к , а затем к , в итоге получим 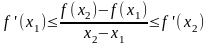. Откуда и следует (9).

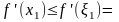
Если же функция - строго выпуклая на интервале , то для произвольно выбранных , , по лемме 1 будем иметь . Поэтому, с учетом установленной выше (нестрогой) монотонности производной , по теореме Лагранжа получим 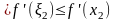, где 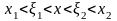. Таким образом, строгая выпуклость функции влечет строгую монотонность ее производной , точнее гарантирует, что она является возрастающей на интервале функцией. Следовательно, необходимость доказана.

Докажем достаточность. Пусть производная функции неубывает (возрастает) на интервале . Докажем, что функция является выпуклой (строго выпуклой). Пусть 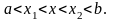Тогда по теореме Лагранжа: 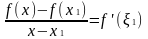, где 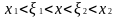. Так как производная не убывает (возрастает) на интервале , то ( 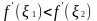), а значит, имеет место и неравенство (2), которое в силу леммы 1 и произвольности точек 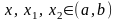гарантирует выпуклость (строгую выпуклость) функции на □

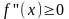
Из теоремы 1 с учетом известных условий монотонности получим такое Следствие. Для того, чтобы дважды дифференцируемая на интервале функция была выпуклой на этом интервале необходимо и достаточно, чтобы 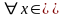. Если же , то этого достаточно, чтобы функция была строго выпуклой на интервале .

Отметим без доказательства еще один интуитивно ясный, геометрический критерий выпуклости (строгой выпуклости) дифференцируемой функции.

Теорема 2. Дифференцируемая на интервале функция является выпуклой на нем тогда и только тогда, когда ее график всеми своими точками лежит не ниже любой проведенной к нему касательной. В свою очередь для строгой выпуклости дифференцируемой на интервале функции необходимо и достаточно, чтобы все точки ее графика лежали выше любой проведенной к нему касательной за исключением самой точки касания.