
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
Теорема
2. Пусть
функция
и все ее производные до порядка
включительно являются непрерывными
функциями на отрезке
 с концами в точках
и
,
а во внутренних точках этого отрезка
существует конечная производная
с концами в точках
и
,
а во внутренних точках этого отрезка
существует конечная производная
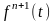 .
Тогда, для любой непрерывной на этом
отрезке функции
,
дифференцируемой во внутренних точках
этого отрезка и имеющей в каждой из этих
точек отличную от нуля производную,
существует такая точка
.
Тогда, для любой непрерывной на этом
отрезке функции
,
дифференцируемой во внутренних точках
этого отрезка и имеющей в каждой из этих
точек отличную от нуля производную,
существует такая точка
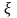 ,
лежащая между точками
и
,
что остаточный член в формуле Тейлора
может быть записан в виде
,
лежащая между точками
и
,
что остаточный член в формуле Тейлора
может быть записан в виде
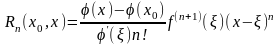 .
(1)
.
(1)
Д
о к а з а т е л ь с т в о. На отрезке
с концами в точках
и
рассмотрим функцию переменной
 :
:
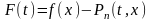 ,
где
,
где
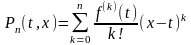
 .
.
Из условий теоремы следует, что на отрезке функция обладает теми же свойствами, что и функция . Точнее, на отрезке функции и удовлетворяют всем условиям теоремы Коши о среднем значении для дифференцируемых функций.
По
этой теореме между точками
и
найдется такая точка
,
что
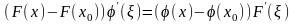 (2)
(2)
Поскольку
 ,
(3) то нетрудно
видеть, что
,
(3) то нетрудно
видеть, что
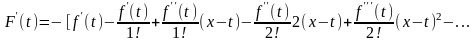
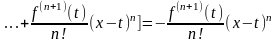 .
(4)
.
(4)
К
тому же, как следует из (3),
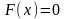 (5) и
(5) и
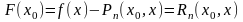 (6) Из
формул (2), (4) – (6) имеем :
(6) Из
формул (2), (4) – (6) имеем :
 .
В свою очередь отсюда, с учетом того,
что по условию теоремы
.
В свою очередь отсюда, с учетом того,
что по условию теоремы
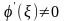 (
- внутренняя точка отрезка
),
получим искомое равенство (1) □
(
- внутренняя точка отрезка
),
получим искомое равенство (1) □
Следствие.
Если на
отрезке с концами в точках
и
функция
и все ее производные до порядка
включительно являются непрерывными
функциями, а во внутренних точках этого
отрезка существует конечная производная
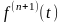 ,
то остаточный член в формуле Тейлора
,
то остаточный член в формуле Тейлора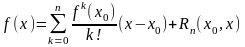 (7) может
быть записан, как в форме Коши:
(7) может
быть записан, как в форме Коши:
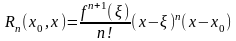 ,
(8)
так и в форме
Лагранжа:
,
(8)
так и в форме
Лагранжа:
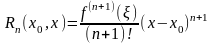 (9) (здесь
лежит между точками
и
,
при этом
является, вообще говоря, разной в формулах
(8) и
(9)).
(9) (здесь
лежит между точками
и
,
при этом
является, вообще говоря, разной в формулах
(8) и
(9)).
Д
о к а з а т е л ь с т в о. Формула (8) вытекает
из формулы (1), если в ней положить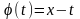 .
В свою очередь, формула (9) вытекает из
той же формулы (1), если в последней
положить
.
В свою очередь, формула (9) вытекает из
той же формулы (1), если в последней
положить
 .
Таким образом, если выполнены условия
следствия из теоремы 2, то формулу Тейлора
для функции
можно записать как в виде
.
Таким образом, если выполнены условия
следствия из теоремы 2, то формулу Тейлора
для функции
можно записать как в виде
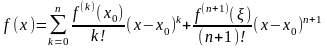 (10)
(формула
Тейлора с остаточным членов в форме
Лагранжа),
так и в виде
(10)
(формула
Тейлора с остаточным членов в форме
Лагранжа),
так и в виде
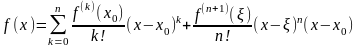 (11)
(формула
Тейлора с остаточным членом в форме
Коши)□
(11)
(формула
Тейлора с остаточным членом в форме
Коши)□
Разложение элементарных функций по формуле Тейлора.
Если
,
то формула Тейлора функции
имеет особенно простой вид:
 (1)
(1)
В этом случае она называется формулой Маклорена. Остаточный член в ней в форме Пеано, Лагранжа и Коши, соответственно, имеет вид
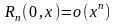 ,
,
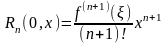 ,
,
и
 .
.
Укажем разложения некоторых элементарных функций по формуле Маклорена.
.
Пусть
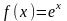 .
Эта функция имеет производные любого
порядка и в любой точке
(в таких случаях говорят, что функция
бесконечно
дифференцируема
на всей числовой оси).
.
Эта функция имеет производные любого
порядка и в любой точке
(в таких случаях говорят, что функция
бесконечно
дифференцируема
на всей числовой оси).
Как
известно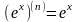 .
Поэтому формула Маклорена функции
.
Поэтому формула Маклорена функции
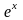 имеет вид (
имеет вид ( ):
):
 ,
где остаточный член можно записать в
любой из форм:
,
где остаточный член можно записать в
любой из форм:
( в форме Пеано)
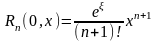 (
в форме
Лагранжа)
и
(
в форме
Лагранжа)
и
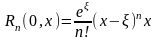 (в форме
Коши), где
точка
в каждой из двух последних формул лежит
между точками
и
(в форме
Коши), где
точка
в каждой из двух последних формул лежит
между точками
и
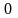 .
.
.
Пусть
 .
Так как эта функция бесконечно
дифференцируема на всей вещественной
оси и
.
Так как эта функция бесконечно
дифференцируема на всей вещественной
оси и
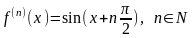 ,
то
,
то
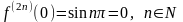 ;
;
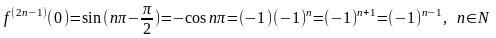 и, следовательно,
и, следовательно,
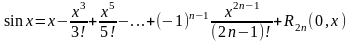 .
При этом остаточный член в форме Пеано
имеет вид:
.
При этом остаточный член в форме Пеано
имеет вид:
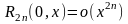 ,
соответственно остаточный член в форме
Лагранжа выглядит следующим образом:
,
соответственно остаточный член в форме
Лагранжа выглядит следующим образом:
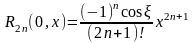 (2), а
остаточный член в форме Коши имеет вид:
(2), а
остаточный член в форме Коши имеет вид:
 (3)
(3)
Замечание
1. Для
доказательства, например, равенства
(2) достаточно заметить, что остаточный
член
 в форме Лагранжа в общем случае имеет
вид:
в форме Лагранжа в общем случае имеет
вид:
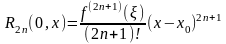 ,
а затем
убедиться в том, что для функции
имеют место равенства
,
а затем
убедиться в том, что для функции
имеют место равенства
 .
.
.
Пусть
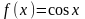 .
Эта функция также бесконечно дифференцируема
.
Эта функция также бесконечно дифференцируема
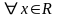 .
Поскольку здесь
.
Поскольку здесь
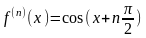 ,
то
,
то
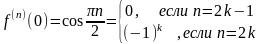 .
Поэтому
имеем,
.
Поэтому
имеем,
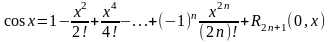 ,
при этом
остаточный член имеет вид:
,
при этом
остаточный член имеет вид:
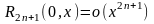 (в форме
Пеано);
(в форме
Пеано);
 (
в форме
Лагранжа);
(
в форме
Лагранжа);
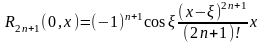 ( в форме
Коши).
( в форме
Коши).
