
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Теоремы Вейерштрасса о непрерывных на отрезке функциях.
Теорема 1 (первая теорема Вейерштрасса). Всякая непрерывная на отрезке функция ограничена на этом отрезке.
Д
о к а з а т е л ь с т в о. Предположим
противное. Тога для любого натурального
найдется такая точка
 ,
что
,
что
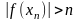 (1). Так как последовательность
ограничена (
(1). Так как последовательность
ограничена (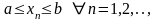 ),
то по теореме Больцано-Вейерштрасса
она содержит сходящуюся подпоследовательность
.
Пусть
),
то по теореме Больцано-Вейерштрасса
она содержит сходящуюся подпоследовательность
.
Пусть
 при
при
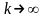 .
.
Очевидно,
что
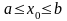 (для того, чтобы убедиться в этом
достаточно в неравенствах
(для того, чтобы убедиться в этом
достаточно в неравенствах
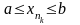 перейти к пределу при
).
Поэтому в силу непрерывности функции
на отрезке
перейти к пределу при
).
Поэтому в силу непрерывности функции
на отрезке
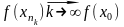 .
Следовательно, последовательность
.
Следовательно, последовательность
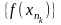 ограничена, что, противоречит тому, что
согласно (1)
ограничена, что, противоречит тому, что
согласно (1)
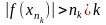
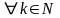 □
□
Пусть
функция
определена
на множестве
.
Далее полагаем
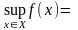
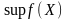 и
и
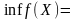
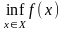 .
.
Теорема
2 (вторая
теорема Вейерштрасса). Всякая
непрерывная
на отрезке
функция
достигает на нем своих точных верхней
и нижней граней, т.е. существуют такие
точки
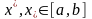 ,что
,что
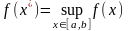 ,
,
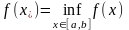 .
.
Д
о к а з а т е л ь с т в о. Докажем, например,
утверждение теоремы относительно точной
верхней грани.
Доказательство
проведем от противного. А именно, положим
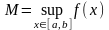 и предположим, что
и предположим, что
 .
Тогда, очевидно, функция
.
Тогда, очевидно, функция
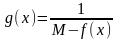 будет непрерывной на отрезке
.
Поэтому по теореме 1 она будет ограниченной
на этом отрезке. В частности, найдется
такое
будет непрерывной на отрезке
.
Поэтому по теореме 1 она будет ограниченной
на этом отрезке. В частности, найдется
такое
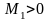 ,
что
,
что
 .
Следовательно
.
Следовательно
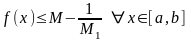 ,
а это противоречит тому, что
□
,
а это противоречит тому, что
□
Замечание
1. Теорема 2
по сути гласит, что во множестве значений
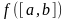 непрерывной на отрезке
функции
имеется
наибольший и наименьший элементы. Они,
соответственно, называются наибольшим
и наименьшим значениями функции, при
этом точки
непрерывной на отрезке
функции
имеется
наибольший и наименьший элементы. Они,
соответственно, называются наибольшим
и наименьшим значениями функции, при
этом точки
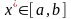 и
и
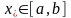 ,
в которых функция
принимает эти значения, называются,
соответственно точкой максимума и
точкой минимума функции
на отрезке
.
Теорему 2, таким образом, можно рассматривать
как теорему о существовании точек
максимума и минимума непрерывной на
отрезке функции.
,
в которых функция
принимает эти значения, называются,
соответственно точкой максимума и
точкой минимума функции
на отрезке
.
Теорему 2, таким образом, можно рассматривать
как теорему о существовании точек
максимума и минимума непрерывной на
отрезке функции.
Наибольшее
и наименьшее значения функции
на отрезке
обычно обозначаются символами
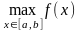 и
и

Из
второй теоремы Вейерштрасса с учетом
следствия из второй теоремы Больцано-Коши,
вытекает такое Следствие.
Множество
значений непрерывной на отрезке
функции
является отрезком
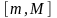 ,
где
,
где
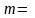 ,
,
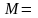 .
.
Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
Теорема 3 (критерий непрерывности монотонной функции). Для того, чтобы монотонная на отрезке функция была непрерывной на нем, необходимо и достаточно, чтобы множество ее значений было отрезком.
Теорема 4 (об обратной функции к непрерывной, строго монотонной). Пусть функция непрерывна и строго монотонна на отрезке . Тогда существует обратная к ней функция , которая является непрерывной и строго монотонной в том же смысле, что и функция .
Следствие.
Пусть
функция
непрерывна и строго монотонна на
произвольном промежутке
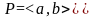 .
Тогда обратная к ней функция непрерывна
и строго монотонна в том же смысле на
промежутке
.
Тогда обратная к ней функция непрерывна
и строго монотонна в том же смысле на
промежутке
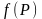 .
.
Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
n°1. Понятие производной.
Пусть
и
.
Точка
называется внутренней
точкой
множества
,
если она принадлежит ему вместе с
некоторой своей окрестностью, т.е.
существует такая окрестность
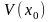 точки
,
что
точки
,
что
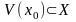 .
.
Пусть
теперь функция
определена на множестве
и
- внутренняя точка множества
.
Тогда существует такая окрестность
точки
,
что
и, следовательно, функция
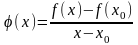 определена на множестве
определена на множестве
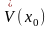 и
– точка сгущения этого множества. Таким
образом, корректно следующее Определение
1. Если
существует предел
и
– точка сгущения этого множества. Таким
образом, корректно следующее Определение
1. Если
существует предел
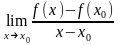 ,
то он называется производной
функции
в точке
.
,
то он называется производной
функции
в точке
.
Производная
функции
(
)
в точке
обозначается одним из последующих
символов: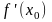 ,
,
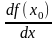 ,
,
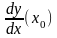 ,
,
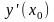 ,
при этом если ясно, в какой точке
рассматривается производная, то для ее
обозначения используют символы:
,
при этом если ясно, в какой точке
рассматривается производная, то для ее
обозначения используют символы:
 ,
,
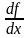 ,
,
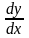 ,
,
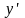 .Таким
образом,
.Таким
образом,
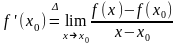 (1)
(1)
Замечание
1. Если
положить
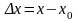 ,
,
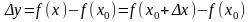 ,
то теорема о пределе суперпозиции
позволяет также определить производную
с помощью любого из равенств:
,
то теорема о пределе суперпозиции
позволяет также определить производную
с помощью любого из равенств:
 (2),
(2),
 (3).
(3).
Величины
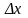 и
и
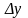 называют, соответственно, приращением
аргумента и приращением функции в точке
.
В соответствии с равенством (3), можно
сказать, что производная
равна пределу отношения приращения
функции (в точке
)
к приращению аргумента.
называют, соответственно, приращением
аргумента и приращением функции в точке
.
В соответствии с равенством (3), можно
сказать, что производная
равна пределу отношения приращения
функции (в точке
)
к приращению аргумента.
Замечание
2. Определение
производной выше было дано в предположении,
что точка
- внутренняя точка области определения
функции
.
Если же точка
не является внутренней точкой множества
,
но принадлежит этому множеству вместе
с некоторой своей односторонней
окрестностью
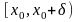 ,
или
,
или
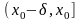 ,
то можно ввести понятие односторонней
производной:
,
то можно ввести понятие односторонней
производной:
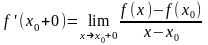 (правая производная),
(правая производная),
 (левая производная).
(левая производная).
Замечание 3. В определении производной не требуется, чтобы предел (1) был конечным. Если предел (1) равен или , то производная называется бесконечной.
Теорема 1. Пусть функция определена в окрестности точки и имеет в этой точке конечную производную. Тогда она непрерывна в этой точке.
Д о к а з а т е л ь
с т в о. Достаточно заметить, что
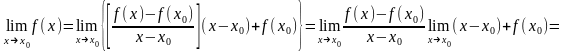
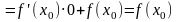 □
□
n°2.
Геометрический смысл производной.
Производная
функции
в точке
– тангенс угла наклона касательной к
графику этой функции в точке
 (подробнее на лекции и в учебниках).
(подробнее на лекции и в учебниках).
n°3. Физический смысл производной Значение производной в точке численно равно мнгновенной скорости изменения функции
Уравнение касательной к графику функции в данной точке.
Определение. Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f(x0). Тогда прямая, проходящая через точку (x0; f(x0)), имеющая угловой коэффициент f ’(x0), называется касательной. А что будет, если производная в точке x0 не существует? Возможны два варианта: Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0). Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).
Уравнение касательной. Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f(x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением: y = f ’(x0) · (x − x0) + f(x0). Здесь f ’(x0) — значение производной в точке x0, а f(x0) — значение самой функции.
