
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Множества и действия над ними.
Ту или иную совокупность (класс, семейство) рассматриваемых объектов называют множеством, а соответствующие объекты – элементами или точками этого множества.
Множество, состоящее из конечного числа элементов, называется конечным, в противном случае оно называется бесконечным.
К числу множеств удобно отнести и, так называемое, пустое множество, которое по определению не содержит ни одного элемента.
Если
каждый элемент множества
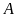 является также и элементом множества
является также и элементом множества
 ,
то множество
называется подмножеством
множества
,
(
,
то множество
называется подмножеством
множества
,
( ).
).
Множества
и
называют равными
друг другу (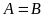 )
, если они состоят из одних и тех же
элементов или, иначе, если
)
, если они состоят из одних и тех же
элементов или, иначе, если
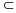 и
.
и
.
Объединением
множеств
и
называется множество
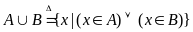 .
.
Пересечением
множеств
и
называется множество
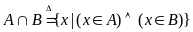 .
.
Очевидно, имеют место следующие свойства операций ∪ и ∩:
а) (коммутативность
операции
∪);
(коммутативность
операции
∪);
б) (коммутативность
операции
∩);
(коммутативность
операции
∩);
в)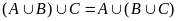 (ассоциативность
операции
∪);
(ассоциативность
операции
∪);
г)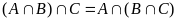 (ассоциативность
операции
∩);
(ассоциативность
операции
∩);
д)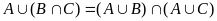 и
и
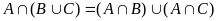 (дистрибутивные
свойства операций
∪
и
∩);
(дистрибутивные
свойства операций
∪
и
∩);
Разностью
между множеством
и множеством
называется множество
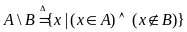 .
.
Прямым
(или
декартовым)
произведением
множеств
 и
и
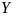 называется множество всех упорядоченных
пар
называется множество всех упорядоченных
пар
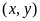 таких, что
таких, что
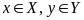 .
.
Прямое
произведение множеств
и
обозначается
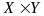 .
Отметим, что вообще говоря,
.
Отметим, что вообще говоря,
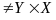 .
.
Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
Пусть
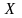 и
и
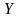 – произвольные множества. Правило
– произвольные множества. Правило
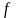 ,
по которому каждому элементу
,
по которому каждому элементу
 ставится в соответствие определенный,
и при том единственный, элемент
ставится в соответствие определенный,
и при том единственный, элемент
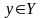 называется отображением
множества
во множество
,
при этом множество
называется областью
определения
отображения
,
а множество
- областью
значений
этого отображения.
называется отображением
множества
во множество
,
при этом множество
называется областью
определения
отображения
,
а множество
- областью
значений
этого отображения.
Если
элемент
отображением
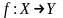 сопоставляется
элементу
,
то элемент
сопоставляется
элементу
,
то элемент
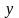 называют образом
элемента
называют образом
элемента
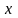 при отображении
или значением
отображения
в точке
и обозначают
при отображении
или значением
отображения
в точке
и обозначают
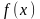 ,
при этом пишут
,
при этом пишут
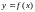 ,
а сам элемент
,
который отображением
сопоставляется элементу,
называют прообразом
элемента y
при отображении
.
,
а сам элемент
,
который отображением
сопоставляется элементу,
называют прообразом
элемента y
при отображении
.
(Подчеркнем,
что образ
элемента
при отображении
(по
определению отображения) определяется
однозначно, а прообразов элемента
при том же отображении может быть
несколько. Множество всех прообразов
элемента
при отображении
обозначается
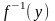 ).
).
Множество
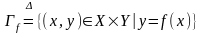 называется графиком
отображения
.
называется графиком
отображения
.
Пусть
задано отображение
и множество
 .
Определим
новое отображение
.
Определим
новое отображение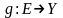 ,
полагая, что
,
полагая, что
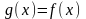
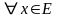 .
Так определенное отображение
.
Так определенное отображение
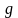 называется
сужением
отображения
на
множество
называется
сужением
отображения
на
множество
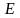 (обозначается
(обозначается
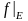 ).
).
Образом
множества
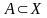 при
отображении
называют множество
при
отображении
называют множество
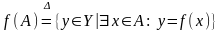 .
.
Отображения
и
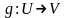 называют равными
друг другу и пишут
называют равными
друг другу и пишут
 ,
если
,
если
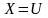 и
и
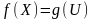 .
.
Отображение будем называть
а)
функцией,
если
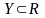 (в частности, отображение
(в частности, отображение
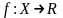 ,
где
– произвольное, необязательно числовое
множество, является функцией)
,
где
– произвольное, необязательно числовое
множество, является функцией)
б)
числовой
функцией
или функцией
одной переменной,
если
и
 .
.
Пусть
даны отображения
и
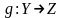 .
Новое отображение
.
Новое отображение
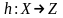 ,
определенное по следующему правилу:
,
определенное по следующему правилу:
 называют
суперпозицией
отображений
и
.
называют
суперпозицией
отображений
и
.
Суперпозицию
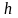 отображений
и
обычно обозначают символом
отображений
и
обычно обозначают символом
 (таким образом,
(таким образом,
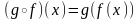 ),
при этом если оба отображения
и
являются функциями, то их суперпозицию
называют сложной
функцией.
),
при этом если оба отображения
и
являются функциями, то их суперпозицию
называют сложной
функцией.
