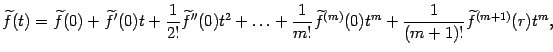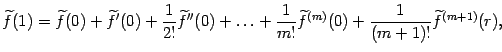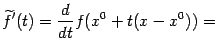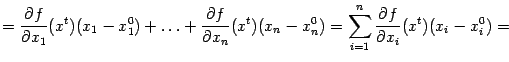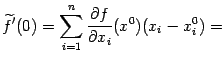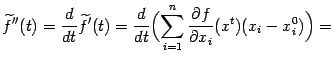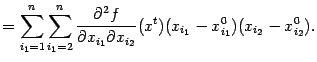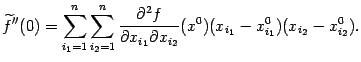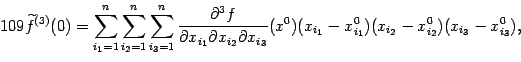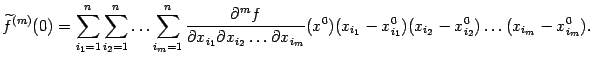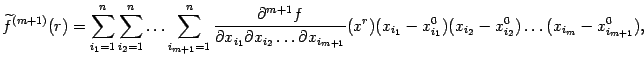10. Остаточный член формулы Тейлора

     В форме Лагранжа:

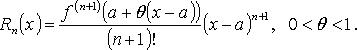
     В форме Пеано:

при

  Многочлен Тейлора порядка n

11. Вывод формулы Тейлора

Предположим, что в рассматриваемой области функция имеет все частные производные до порядка включительно. Рассмотрим прямую , соединяющую фиксированную внутреннюю точку с произвольной точкой и будем предполагать, что все точки отрезка, соединяющего с , также принадлежат :

при 

Рассмотрим ограничение функции на прямую (точнее, на её часть, лежащую в пределах области ) и параметризуем это ограничение параметром . Получим функцию одного переменного :

К функции можно применить обычную (приведённую выше) формулу Тейлора в точке :

где  -- некоторая точка отрезка между 0 и . Если , то также принадлежит отрезку . Отсюда при получаем

(9.1)

где .

Очевидно, что . Посмотрим, как производные

выражаются через частные производные функции .

Для нахождения воспользуемся формулой производной сложной функции:

При получаем

	(9.2)
	(9.3)

Вычислим теперь , для чего найдём :

Положив в этой формуле , получаем:

(9.4)

Каждое последующее дифференцирование, как нетрудно понять, будет увеличивать на единицу количество суммирований от 1 до , порядок частных производных функции , вычисленных в точке , а также количество сомножителей-биномов вида . Для третьей производной получаем

а для производной порядка  --

(9.5)

Правая часть формулы (9.5) содержит слагаемых, в каждом из которых множитель. Точно так же выписывается и выражение, задающее :

(9.6)

где .

12. Формулы Маклорена некоторых элементарных функций.

1) f(x)=e^x

f '(x)=f "(x)=…=f(n+1)(x)=e^x

f(0)=f '(0)=f "(0)=…=f(n+1)(0)=1

(5)

2) f(x)=sinx

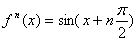
(6)

3) f(x)=cosx

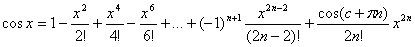(7)

13. Экстремум необходимое и достаточное условие существования экстремума функции.

Теорема 1 (необходимое условие существования экстpeмума). Если дифференци­руемая функция y=f(x) имеет в точке x = х₂ максимум или мини­мум, то ее производная обращается в нуль в этой точке, т. e. f' (х₂) = 0.

ОПРЕДЕЛЕНИЕ. Функция называется возрастающей (неубывающей) на интервале если для любых 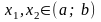таких, что 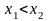значения функции и удовлетворяют неравенству ¹ ( ).

Функция называется убывающей (невозрастающей) на интервале если для любых таких, что значения функции и удовлетворяют неравенству ² ( ).

ТЕОРЕМА 1 (необходимое и достаточное условия возрастания (убывания) функции). Пусть функция дифференцируема на интервале . Тогда

1) если функция возрастает (убывает) на , то на этом интервале ее производная неотрицательна (неположительна),

т.е. , ( , );

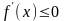2) если производная на интервале положительна (отрицательна), т.е.

, ( , ),

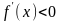то функция на возрастает (убывает).

14. Выпуклость и вогнутость функции, точка перегиба

Определение 7. Говорят, что кривая выпуклая (обращена выпуклостью вверх) на интервале (a, b), если в каждой точке этого интервала касательная расположена выше кривой. Говорят, что кривая вогнутая (обращена выпуклостью вниз) на интервале (a, b), если в каждой точке этого интервала касательная расположена ниже кривой.

Теорема 22.

Пусть функция y = f(x) дважды дифференцируема на интервале (a, b). Если f''(x) < 0 (f''(x ) > 0) на (a, b), то кривая y = f(x) выпуклая (вогнутая) на (a, b).

Определение 8. Точка на кривой, отделяющая выпуклую часть от вогнутой, называется точкой перегиба.

Теорема 23.

П усть функция y = f(x) дважды дифференцируема на (a, b), кроме, быть может, числа x₀ (a,b). При x = x₀ функция f либо непрерывна и не имеет второй производной, либо дважды дифференцируема и f''(x₀) = 0. Если при переходе через x₀ вторая производная функции f меняет знак, то (x₀, f(x₀)) – точка перегиба.

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1   Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .     

15. Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1   Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .     

Производные:

Графики

Рис. 5. Графики гиперболических функций     и   . Рис. 3. Графики гиперболических функций     и   . График гиперболического косинуса называется цепной линией, которая является линией провисания тяжёлой нити, подвешенной в двух точках.

Гиперболический синус     и гиперболический косинус     определяются аналитическими выражениями

Эти функции определены и непрерывны на всей числовой оси и тождественно удовлетворяют следующим соотношениям, которые легко проверяются непосредственным вычислением:

  Гиперболический тангенс     и гиперболический котангенс     определяются формулами

и представляют собой нечетные функции:

1

2