
- •30. Собственные векторы линейного преобразования. Вид матрицы линейного преобразования в базисе из собственных векторов
- •31. Диагонализируемые линейные преобразования. Достаточные условия диагонализируемости линейного преобразования
- •32. Симметричные линейные преобразования, их свойства
- •33. Расстояние между точками на числовой прямой, окрестность точки. Определение функции
- •34. Предел последовательности: определение, свойства. Число
- •35. Предел функции: определение, свойства. Замечательные пределы
- •36. Непрерывность функции в точке: определение, теорема о приращении
- •37. Непрерывные функции, их свойства
- •38. Свойства непрерывных на замкнутом отрезке функций
- •39. Точки разрыва
- •40. Бесконечно малые величины
- •41. Определение производной. Геометрический смысл производной. Связь непрерывности и дифференцируемости функции
- •42. Правила дифференцирования. Производная сложной функции
- •43. Дифференциал: определение, геометрический смысл
- •48. Достаточные условия существования экстремума в терминах первой и второй производной
39. Точки разрыва
Определение
Точка называется точкой разрыва функции , если не непрерывна в , т.е. если
1. или
(тогда
![]() )
)
2. или
![]()
3. или
![]()
Определение (предел справа)
![]() ,
если для любой последовательности
,
такой, что
,
если для любой последовательности
,
такой, что
![]() и
и
![]() ,
последовательность
,
последовательность
![]() значений функции имеет предел
.
значений функции имеет предел
.
Определение (предел слева)
![]() для
любой
:
и
для
любой
:
и
![]() последовательность
последовательность
![]()
Определение
называется точкой разрыва 1-го рода
для функции
,
если
- точка разрыва, но существуют конечные
односторонние пределы (![]() )
)
![]() и
и
![]() .
.
Определение
называется точкой разрыва 2-го рода
для функции
,
если хотя бы один из односторонних
пределов
и
не существует (или
![]() ).
).
[_]
40. Бесконечно малые величины
Определение
Функция
называется бесконечно малой
функцией (или просто бесконечно малой)
в точке
![]() (или при
),
если
(или при
),
если
![]() .
.
Теорема
Алгебраическая сумма и произведение конечного числа бесконечно малых функций при , а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при .
Доказательство
Пусть
и
![]() ,
а
,
а
![]() - ограниченная функция. Тогда
- ограниченная функция. Тогда
![]()
![]()
![]()
Сравнение бесконечно малых функций
Пусть при
функции
![]() и
и
![]() являются бесконечно малыми. Тогда
являются бесконечно малыми. Тогда
1. если
 ,
то
- бесконечно малая более высокого
порядка, чем
,
то
- бесконечно малая более высокого
порядка, чем
2. если
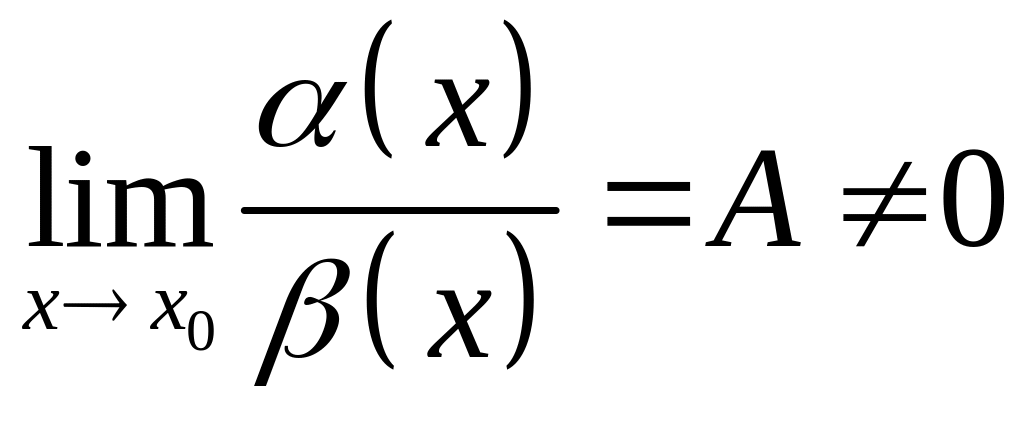 ,
то
и
- бесконечно малые одного порядка
,
то
и
- бесконечно малые одного порядка
3. если
 ,
то
и
- эквивалентные бесконечно малые (
,
то
и
- эквивалентные бесконечно малые (![]() )
)
4. если
 ,
то
- бесконечно малая
-го
порядка относительно
,
то
- бесконечно малая
-го
порядка относительно
[_]
41. Определение производной. Геометрический смысл производной. Связь непрерывности и дифференцируемости функции
Определение
Рассмотрим функцию
.
Пусть
- фиксированная точка из
![]() и существует отрезок
и существует отрезок
![]() .
Тогда для точек
и
.
Тогда для точек
и
![]()
![]() определено приращение
определено приращение
![]() .
Производная
.
Производная

называется дифференцируемой, если
![]() существует для
существует для
![]() .
.
Геометрический смысл
Касательная к кривой
в точке
![]() - это предельное положение секущей
- это предельное положение секущей
![]() при стремлении точки
к точке
по кривой
.
Пусть
при стремлении точки
к точке
по кривой
.
Пусть
 .
Из
.
Из
![]() :
:

При
![]() .
Тогда
.
Тогда

![]()
Т.е.
![]() - тангенс угла наклона касательной к
кривой
в точке
(угловой коэффициент касательной).
- тангенс угла наклона касательной к
кривой
в точке
(угловой коэффициент касательной).
Уравнение касательной
![]()
Теорема
Если для функции
в точке
существует производная
![]() ,
тогда
непрерывна в точке
.
,
тогда
непрерывна в точке
.
Доказательство
Пусть
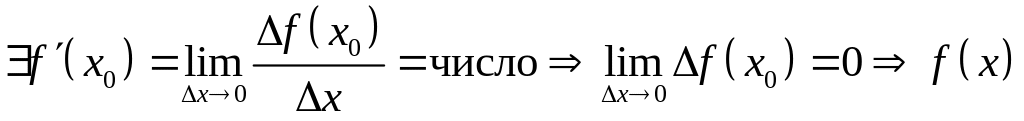 непрерывна в
.
непрерывна в
.
[_]
42. Правила дифференцирования. Производная сложной функции
Правила дифференцирования
Пусть
![]() ,
,
![]()
1.
![]()
2.
![]()
![]()
3.

Производная сложной функции
Пусть , - дифференцируемые функции. Тогда
![]()
Доказательство

![]()
[_]
43. Дифференциал: определение, геометрический смысл
Определение
![]() ,
,
где
![]() - приращение. Дифференциал зависит от
и от
- приращение. Дифференциал зависит от
и от
![]() .
.
Геометрический смысл
Из
![]() :
:
![]()
Следовательно,
![]() - приращение касательной к кривой
в точке
.
- приращение касательной к кривой
в точке
.
Почему
?
Рассмотрим функцию
![]() .
.
![]()
Новое обозначение производной:
![]()
Что дает ? Из чертежа
![]()
Доказывается, что при
 .
.
Определение
- главная (основная) часть приращения
функции
![]() :
:
![]()
[_]
44. Определения производных высших порядков
Пусть существует . Тогда
![]()
![]()
[_]
45. Правило Лопиталя
Пусть
 или
или
![]() .
Если
.
Если
 ,
то
,
то
 .
.
[_]
46. Исследование функции на монотонность
Теорема
Пусть функция
возрастает (убывает) на некотором
интервале
![]()
![]() (
(![]() на
на
Доказательство
Пусть
возрастает, тогда при
![]()

 для
для
![]()
![]() Используем теорему Лагранжа. Пусть
непрерывна и дифференцируема на
Используем теорему Лагранжа. Пусть
непрерывна и дифференцируема на
![]() .
Тогда
.
Тогда
![]() :
:
![]()
Пусть
для
![]() .
Возьмем
.
Возьмем
![]() ,
,
![]() .
По теореме Лагранжа
.
По теореме Лагранжа
![]()
возрастает.
[_]
47. Экстремум функции. Теорема Ферма. Необходимое условие существования экстремума
Определение
называется точкой (локального)
![]() (
(![]() )
функции
,
если существует окрестность точки
-
)
функции
,
если существует окрестность точки
-
![]() такая, что
такая, что
![]() (
(![]() )
для
)
для
![]() .
.
Теорема Ферма
Пусть
имеет
(
)
в точке
и ее производная
непрерывна, тогда в точке экстремума
![]() .
.
Доказательство
Пусть
- точка максимума, тогда до
возрастает
при
![]() (см. билет №46), а после
убывает
при
(см. билет №46), а после
убывает
при
![]() (см. билет №46). Так как
непрерывна, то
.
(см. билет №46). Так как
непрерывна, то
.
Следствие (необходимое условие существования экстремума функции)
Для существования экстремума функции в точке необходимо (но не достаточно), чтобы или не существовала.
[_]
