30. Собственные векторы линейного преобразования. Вид матрицы линейного преобразования в базисе из собственных векторов

Пусть - линейное преобразование.

Определение

Вектор из называется собственным вектором (СВ) линейного преобразования , соответствующим собственному значению (СЗ) , если

Нахождение СВ линейного преобразования

Пусть - базис в

Следовательно СВ линейного преобразования - это СВ матрицы .

Теорема

Пусть для линейного преобразования существует базис , состоящий из СВ линейного преобразования : . Тогда

и матрица в этом базисе будет иметь вид

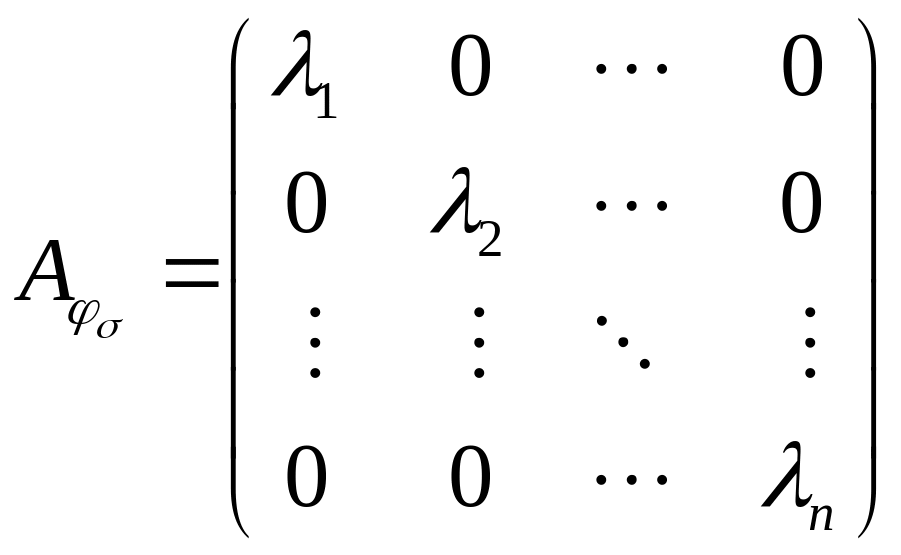
т.е. будет иметь диагональный вид, причем на ее диагонали будут стоять СЗ линейного преобразования .

Доказательство

Так как

то по определению матрицы линейного преобразования

Теорема (обратная)

Если в некотором базисе матрица линейного преобразования имеет диагональный вид, то - базис из СВ линейного преобразования .

[_]

31. Диагонализируемые линейные преобразования. Достаточные условия диагонализируемости линейного преобразования

Определение

Линейное преобразование называется диагонализируемым, если в существует базис, в котором матрица диагональная.

Этот базис будет состоять из СВ (см. билет №30)

Достаточные условия диагонализируемости линейного преобразования

Теорема

СВ линейного преобразования, соответствующие различным СЗ, линейно независимы.

Следствие

Пусть - линейное преобразование и характеристический многочлен его матрицы в некотором базисе имеет различных действительных корней. Тогда - диагонализируемое линейное преобразование.

(Тогда имеет линейно независимых СВ существует базис , состоящий из СВ).

[_]

32. Симметричные линейные преобразования, их свойства

Определение

Пусть - линейно преобразование. называется симметричным линейным преобразованием

Эквивалентное определение: - симметричное линейное преобразование в ортонормированном базисе имеет симметричную матрицу:

Свойства

1. Характеристический многочлен матрицы симметричного линейного преобразования имеет действительных корней.

2. СВ симметричного линейного преобразования с различными СЗ ортогональны

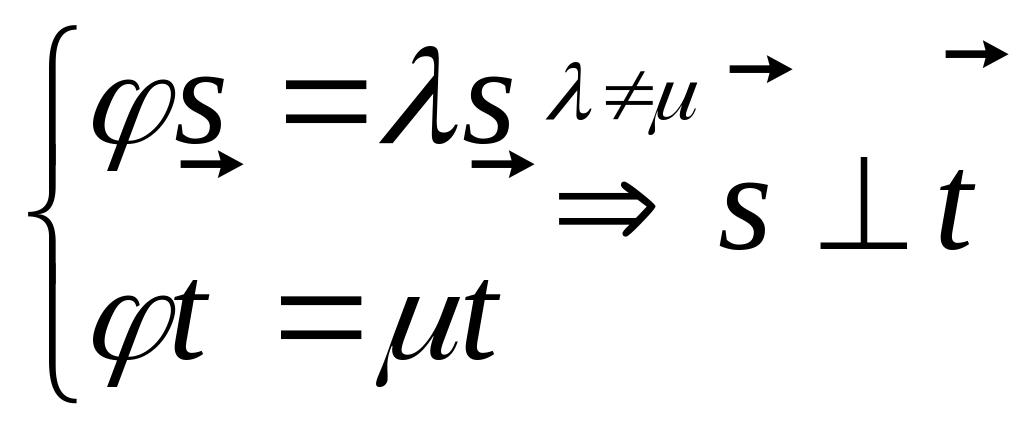
3. Для симметричного линейного преобразования существует ортонормированный базис из СВ .

[_]

33. Расстояние между точками на числовой прямой, окрестность точки. Определение функции

Расстояние между точками на числовой прямой

Расстояние между точками на числовой прямой определяется как

Окрестность точки

Определение

Пусть число , - точка на числовой оси ( ). -окрестностью точки называется

Определение функции

Пусть и - некоторые числовые множества. Функцией называется множество упорядоченных пар чисел таких, что , , и каждое входит в одну и только одну пару этого множества, а каждое входит, по крайней мере, в одну пару. При этом говорят, что числу поставлено в соответствие число , и пишут . Число называется значением функции в точке . Переменную называют зависимой переменной, а переменную - независимой переменной (или аргументом), множество - областью определения (или существования) функции, а множество - множеством значений функции.

[_]