1. Аффинное пространство и его простейшие свойства. Примеры.

Определение 25.1. Пусть заданы n-мерное линейное пространство Vⁿ над полем P и не пустое множество Aⁿ , элементы которого будем называть точками. Предположим, что каждой упорядоченной паре точек M, N Aⁿ поставлен в соответствии вектор пространства Vⁿ , обозначаемый , причем выполнены следующие аксиомы.

1^о. Для любой точки M Aⁿ и любого вектора a Vⁿ существует единственная точка N Aⁿ, такая, что = а.

2^о. Для любых трех точек L, M, N Aⁿ имеет место равенство + = (1)

Тогда множество Aⁿ называется n-мерным аффинным пространством, связанным с линейным пространством Vⁿ.

Пример1. Пространство E³ удовлетворяет определению 25.1 при n = 3 и P = R.

Свойства:

1. Для любой точки M Aⁿ вектор 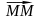- нулевой вектор пространства Vⁿ.

В самом деле, пологая в равенстве (1) L = M, получаем 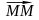+ = , следовательно, = 0.

2. Для любых точек M, N Aⁿ имеем = - . Это вытекает из равенства (1) при L = N и предыдущего следствия.

3. Фиксируем в пространстве Aⁿ какую-либо точку О. тогда каждой точке M Aⁿ будет соответствовать вектор 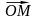Vⁿ , называем радиусом-вектором этой точки. В силу аксиомы 1^о отображение f: Aⁿ Vⁿ, M является биекцией.

4. Для любых А, А1, В, В1 A ⁿ выполняется = тогда и только тогда, когда =

Теорема: для произвольного n-мерного линейного пространства Vⁿ можно построить аффинное пространство Aⁿ, связанное с Vⁿ.

Доказательство: Возьмем в качестве Aⁿ множество Vⁿ, т.е. элементы множества Vⁿ будем называть векторами, и точками. Двум произвольным точкам а, b Aⁿ= Vⁿ, поставим в соответствие вектор = b - a и проверим, будут ли выполняться аксиомы 1^о и 2^о. Пусть а Aⁿ = Vⁿ – произвольная точка и b Vⁿ – произвольный вектор. Требуется доказать существование единственной точки х Aⁿ= Vⁿ, такой, что = b, т.е. x – a = b. Очевидно, что искомой является точка x = a + b, и только она. Для трех произвольных точек а, b Aⁿ= Vⁿ аксиома 2^о выполняется, так как равенство + = равносильно очевидному равенству(b - a) + (c - b) = c – a.

Пример 2. n-мерное аффинное пространство А ⁿ связанное с векторным пространством V ⁿ , называют каноническим аффинным пространством, связанным с векторным пространством V ⁿ . А ⁿ(V ⁿ)

2. Координаты в аффинном пространстве.

Определение 25.2. Аффинной системой координат или репером в аффинном пространстве Aⁿ называется упорядоченная система (О, e₁ , …, ), (1)

состоящая из некоторой точки О Aⁿ и базиса , …, (2)

соответствующего линейного пространства Vⁿ.

Координатами точки М Aⁿ в репере (1) называются координаты х₁, х₂, …,х_п (3) ее радиуса-вектора в базисе (2), т.е. коэффициенты в разложении = х₁е₁ + х₂е₂ + …+ х_пе_п.

Заметим, что координаты точки в заданном репере определены однозначно.

Пусть А_n – n-мерное аффинное пространство, связанное с век. Пространством V ⁿ (О, e₁ , e₂,…, e_n) (4), (О^’, e₁^’ , e₂^’,…, e_n^’) (5) два репера А_n . Пусть заданы координаты (а₁, а₂, …, а_п) точки О^’ в репере (1) и матрица A = перехода от базиса (2) к базису e₁^’ , e₂^’,…, e_n^’ ₍₆₎ и пусть точка M Aⁿ имеет в репере (1) координаты (х₁, х₂, …,х_п ) (3) и в новом репере (5) координаты (х₁^’ , х₂^’,…, х_n^’) (7)

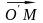Выразим старые координаты (3) точки М через ее новые координаты (7). Для этого введем следующие обозначения: , , . Так как координатный столбец вектора в базисе (2) равен Х – А₁ , а в базисе (6) равен X^’, по формулам преобразования координат вектора имеем: Х – А₁ = AX’ или X = AX’+ А₁ . (9)

Запишем формулы (9) в развернутом виде

или в общем виде , i = 1, 2, …, n.